• Inicio
• Sólido rígido
• Conservación del momento angular

Choque de una partícula con un sólido rígido

En esta página, se describe un ejemplo más de sistema aislado en el que se aplica simultáneamente el principio de conservación del momento lineal y del momento angular.

Descripción

Consideremos una partícula de masa m con velocidad inicial u que choca con sólido rígido en reposo formado por dos partículas iguales A y B de masa M situadas en los extremos de una varilla rígida de longitud 2L y de masa despreciable, tal como se muestra en la figura.
Supondremos que la partícula de masa m choca con la partícula A más cercana. El movimiento del sistema está contenido en una superficie plana en la que se supone que no hay rozamiento.

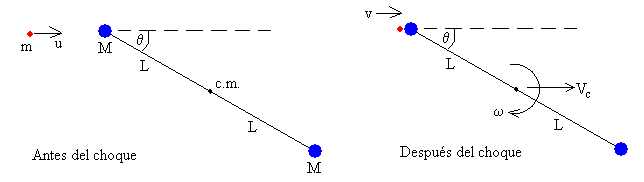
En la figura de la izquierda, se muestra la situación inicial y en la de la derecha la situación final: la partícula lleva una velocidad v, y el sólido describe un movimiento de rotación alrededor de su centro de masas con velocidad angular ω y su centro de masas se traslada con velocidad V_c.

El sistema formado por la partícula y sólido es aislado, la resultante de las fuerzas exteriores es cero, por lo que son aplicables los principios de conservación del momento lineal y angular.

• Principio de conservación del momento lineal

${\displaystyle F_{ext}=\frac{dP}{dt}{F}_{ext}=0P=\text{cte}}$

mu=2MV_c+mv

• Principio de conservación del momento angular

${\displaystyle M_{ext}=\frac{dL}{dt}{M}_{ext}=0L=\text{cte}}$

El momento angular respecto del c.m. antes y después del choque es
mu·Lsinθ=mvLsinθ+I_cω

donde I_c=2ML²es el memento de inercia de las dos partículas A y B respecto de un eje perpendicular a la varilla y que pasa por el c.m. y ω es la velocidad angular de rotación

La definición de coeficiente de restitución e nos proporciona la tercera ecuación

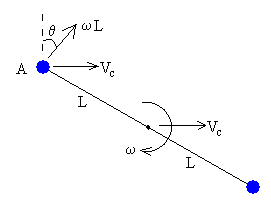La velocidad de la partícula de masa m antes del choque es u y después del choque es v

La partícula A antes del choque está en reposo, después del choque, la componente horizontal de su velocidad es Vc+ωLsinθ

• la velocidad relativa de acercamiento es u-0
• la velocidad relativa de alejamiento es v-( Vc+ωLsinθ)

El coeficiente de restitución e se define

v-( Vc+ωLsinθ)=-e(u-0)

Después de algunas operaciones obtenemos

• La velocidad V_c de traslación del c.m. del sólido

${\displaystyle V_c=\frac{1+e}{2\frac{M}{m}+1+{\sin }^2\theta }u=fuf=\frac{1+e}{2q+1+{\sin }^2\theta }q=\frac{M}{m}}$

• La velocidad angular ω de rotación del sólido rígido de un eje que pasa por el c.m.

${\displaystyle \omega =\frac{f\sin \theta }{L}u}$

• La velocidad v de la partícula después del choque

${\displaystyle v=\left(1-2qf\right)u}$

A continuación, podemos determinar el balance energético de la colisión

${\displaystyle \begin{array}{l}{E}_i=\frac{1}{2}m{u}^2\\ E_f=\frac{1}{2}m{v}^2+\frac{1}{2}2M{V}_c^2+\frac{1}{2}{I}_c{\omega }^2\\ \Delta E=E_f-E_i=\frac{1}{2}m{v}^2+\frac{1}{2}2M{V}_c^2+\frac{1}{2}2M{L}^2{\omega }^2=\\ \frac{1}{2}m{\left(1-2qf\right)}^2{u}^2+\frac{1}{2}2M{f}^2{u}^2+\frac{1}{2}2M{L}^2\frac{f^2{\sin }^2\theta }{L^2}{u}^2-\frac{1}{2}m{u}^2=\\ \frac{1}{2}m{u}^2\left(2q(2q+1+{\sin }^2\theta )f^2-4qf\right)=\\ \frac{1}{2}m{u}^2\frac{2q(e^2-1)}{2q+1+{\sin }^2\theta }\end{array}}$

Ejemplo:

• Velocidad inicial de la partícula u=1.0 m/s

• Cociente de masas q=M/m=1.5
• Ángulo que forma la varilla con la horizontal θ=30º
• Coeficiente de restitución e=0.7
• Longitud de la varilla que une las partículas A y B del sólido 2L=1.0 m

${\displaystyle \begin{array}{l}f=\frac{1+e}{2q+1+{\sin }^2\theta }=\frac{1+0.7}{2·1.5+1+{\sin }^{2}30}=0.4\\ V_c=fu=0.4·1=0.4\text{m/s}\\ \omega =\frac{f\sin \theta }{L}u=\frac{0.4\sin 30}{0.5}=0.4\text{rad/s}\\ v=(1-2qf)u=(1-2·1.5·0.4)·1=-0.2\text{m/s}\end{array}}$

Balance energético

${\displaystyle \begin{array}{l}{E}_i=\frac{1}{2}m{u}^2=\frac{1}{2}1·1^2=0.5\text{J}\\ E_f=\frac{1}{2}m{v}^2+\frac{1}{2}2M{V}_c^2+\frac{1}{2}{I}_c{\omega }^2=\frac{1}{2}1·{0.2}^2+\frac{1}{2}2·1.5·{0.4}^2+\frac{1}{2}(2·1.5·{0.5}^2){0.4}^2=0.32\text{J}\\ \Delta E=E_f-E_i=0.32-0.5=-0.18\text{J}\\ \Delta E=\frac{1}{2}m{u}^2\frac{2q(e^2-1)}{2q+1+{\sin }^2\theta }=\frac{1}{2}1·1^2\frac{2·1.5({0.7}^2-1)}{2·1.5+1+{\sin }^{2}30}=-0.18\text{J}\end{array}}$

Caso particular

Como caso particular tenemos aquél en el que θ=0. Esto es equivalente al choque de dos partículas una de masa m y velocidad u y otra de masa 2M inicialmente en reposo.

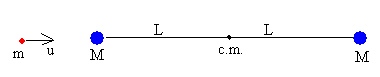
Las ecuaciones que describen este choque son

• Conservación del momento lineal
  mu=2MV_c+mv
• Definición de coeficiente de restitución
  v-V_c=-e·u

Despejamos las incógnitas v y V_c

${\displaystyle \begin{array}{l}{V}_c=\frac{1+e}{1+2q}u\\ v=V_c-eu=\frac{1-2qe}{1+2q}u\end{array}}$

Actividades

Se introduce

• El cociente q=M/m, en el control de edición titulado Cociente masas M/m.
• El coeficiente de restitución e, en el control de edición titulado Coef. de restitución.
• La longitud de la varilla 2L se mantiene fija e igual a 1 m.
• La velocidad u de la partícula incidente se mantiene fija e igual a 1.0 m/s.

Se pulsa el botón titulado Empieza

La partícula incidente se mueve hacia la partícula A del sólido. Choca y observamos el movimiento de la partícula incidente (de color rojo) después del choque, y el movimiento de traslación y de rotación del sólido.

En la parte superior derecha, se nos proporciona los datos relativos a las velocidades

• v de la partícula después del choque
• V_c de traslación del c.m. del sólido
• ω de rotación del sólido alrededor de un eje que pasa por el c.m.

En la parte inferior izquierda, se representa un diagrama en forma de tarta que muestra como se distribuye la energía después del choque. Los sectores representan:

• La energía cinética de la partícula incidente después del choque $E_1=\frac{1}{2}m{v}^2$ (en color rojo).
• La energía cinética de traslación del c.m. del sólido $E_2=\frac{1}{2}M{V}_c^2$ (en color azul).
• La energía cinética de rotación del sólido $E_3=\frac{1}{2}{I}_c{\omega }^2$ (en color gris)

Si el choque es elástico, la energía inicial es igual a la final. Si el choque no es elástico la energía inicial es mayor que la final. Un círculo de mayor radio de color gris claro indica la energía inicial, y el de menor radio dividido en sectores la energía final.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

La partícula se pega al sólido

El estudio de este caso es similar al del proyectil disparado que se incrusta en un disco.

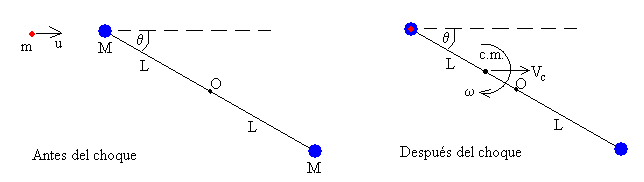
Principio de conservación del momento lineal

mu=(2M+m)V_c

Donde V_c es la velocidad del centro de masas que ahora no coincide con la mitad de la varilla O, sino que está situado a una distancia

${\displaystyle h=\frac{m}{2M+m}L}$

Principio de conservación del momento angular

Calculamos el momento angular respecto del extremo P de la varilla.

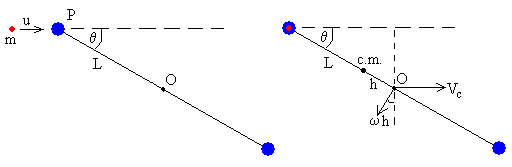
• El momento angular inicial es cero
• El momento angular final es la suma del momento angular debido al movimiento de rotación del sólido alrededor de un eje que pasa por O y del momento angular orbital de O alrededor del extremo P de la varilla.

La velocidad de O es la suma de la velocidad del c.m. V_c y la velocidad de rotación alrededor de un eje que pasa por el c.m. ω×h

El momento angular del sólido respecto a su extremo P es

-I_oω+2M(V_cLsinθ-Lωh)=0

donde I_o=2ML²

Despejamos la velocidad del c.m. V_c de la primera ecuación y la velocidad angular de rotación ω de la segunda.

${\displaystyle V_c=\frac{m}{2M+m}u\omega =\frac{m\sin \theta }{2(M+m)L}u}$

Una alternativa es la de calcular el momento angular respecto del centro de masas.

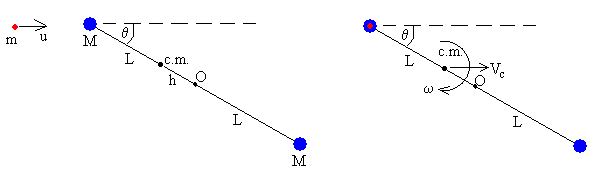
• El momento angular inicial es  mu(L-h)sinθ
• El momento angular final es el sistema formado por el sólido y la partícula pegada a su extremo describiendo un movimiento de rotación  alrededor de un eje que pasa por el c.m.

${\displaystyle \left(2M{L}^2+2M{h}^2+m{(L-h)}^2\right)\omega }$

2ML²+2Mh² es el momento de inercia del sólido respecto de un eje que pasa por el c.m. (teorema de Steiner)

Igualando el momento angular inicial al final, despejamos la velocidad angular de rotación

${\displaystyle \begin{array}{l}mu(L-h)\sin \theta =\left(2M{L}^2+2M{h}^2+m{(L-h)}^2\right)\omega \\ \omega =\frac{m\sin \theta }{2(M+m)L}u\end{array}}$

Referencias

Mungan C. E. Collision of a ball with a barbell and related impulse problems. Eur. J. Phys. 28 (2007) 563-568.

Curso Interactivo de Física en Internet © Ángel Franco García