Dos discos que se acoplan. El momento angular no se conserva
En la página anterior hemos aplicado el principio de conservación del momento angular a dos discos que se acoplan. Los discos se ponen en contacto deslizando el segundo a lo largo del eje del primero. Los dos discos al final giran alrededor del mismo eje.
En esta página, se describe una situación distinta. Los discos giran alrededor de sus respectivos ejes paralelos y se ponen en contacto por sus bordes. Vamos a comprobar que en esta situación no se conserva el momento angular.
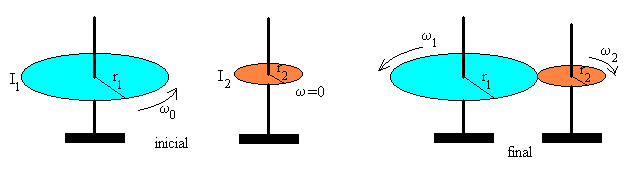
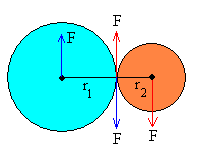
Sean dos discos de masas m1 y m2 y radios r1 y r2, que pueden girar alrededor de ejes paralelos que pasan por sus centros, tal como se muestra en la figura.
En la situación inicial, el primer disco gira alrededor de su eje con velocidad angular inicial ω0. El segundo disco está en reposo. Se acercan los dos discos, manteniendo paralelos sus ejes hasta que sus bordes entran en contacto. En el punto de contacto se originan dos fuerzas iguales y de sentido contrario debido al deslizamiento de una superficie sobre de la otra.
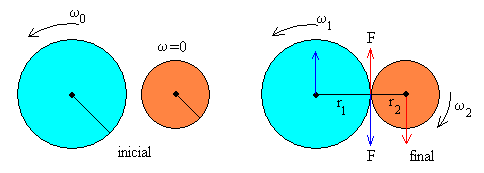
También se han dibujado las fuerzas sobre los ejes de cada uno de los discos, necesarias para impedir la traslación de los mismos.
-
La fuerza F de color azul en el borde del primer disco, cuyo momento es F·r1 frena el este disco, disminuyendo su velocidad angular de rotación ω1.
-
La fuerza F de color rojo en el borde del segundo disco, cuyo momento es F·r2 acelera el este disco, aumentando su velocidad angular de rotación ω2.
Cuando se cumpla la igualdad de las velocidades en el punto de contacto de ambos discos, no habrá deslizamiento entre las dos superficies y los discos girarán con velocidades angulares finales constantes.
Ecuaciones del movimiento
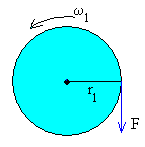 La ecuación del movimiento del primer disco de momento
de inercia I1 es
La ecuación del movimiento del primer disco de momento
de inercia I1 es
La velocidad angular disminuye
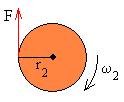 La ecuación del movimiento del segundo disco de momento
de inercia I2 es
La ecuación del movimiento del segundo disco de momento
de inercia I2 es
La velocidad angular aumenta (en valor absoluto)
Cuando se cumpla la igualdad de velocidades en el punto de contacto, no habrá deslizamiento entre las superficies.
ω1·r1=-ω2·r2
Los discos girarán alrededor de sus ejes con velocidad angular constante. El tiempo t que tarda en alcanzarse esta velocidad es
Designando por tf este tiempo
La velocidad angular final constante de cada unos de los discos es
Variación del momento angular
El momento angular inicial es Li=I1·ω0
El momento angular final Lf=I1·ω1f+I2·ω2f
Ambos momentos angulares como puede comprobarse no son iguales. La variación de momento angular se puede calcular a partir del impulso angular
Si consideramos a los dos discos como un sistema, observamos dos clases de fuerzas
 |
|
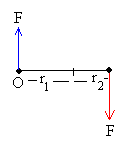 |
El momento de las fuerzas exteriores que actúan sobre el sistema no es cero. Ya que dichos momentos los hemos de calcular con respecto de un único punto. Elijamos el centro del primer disco Mext=F·0 -F·(r1+r2)=-F·r1-F·r2 |
El impulso angular, como podemos comprobar, es igual a la variación del momento angular total final menos el inicial.
La consecuencia de que el momento de las fuerzas exteriores no sea cero es que el momento angular total no permanece constante. Habitualmente olvidamos dibujar las fuerzas sobre los ejes de rotación lo equivocadamente nos conduce a aplicar el principio de conservación del momento angular a este sistema.
Balance energético
Energía cinética de rotación, inicial
La energía final
La variación de energía cinética es
Podemos calcular el trabajo del momento de las fuerzas interiores o de interacción entre los discos F iguales y de sentido contrario que actúan en el punto de contacto. Las fuerzas exteriores que actúan en los ejes de los discos no realizan trabajo alguno.
Calculamos mediante las ecuaciones de la Cinemática, el ángulo girado por cada una de las ruedas desde el momento en que entran en contacto hasta el instante tf, en el que las velocidades angulares de los discos se hacen constantes.
Después de hacer algunas operaciones, comprobaremos que el trabajo realizado por las fuerzas interiores es igual a la variación de energía cinética
W=ΔEk
Ejemplos
Ejemplo1:
-
Radios de los discos r1=1.0 m, r2=0.5 m
-
Masas de los discos m1=1.0 kg, m2=0.8 kg
-
Fuerza de rozamiento entre las superficies en contacto, F=0.1 N
-
Velocidad angular inicial del disco izquierdo, ω0=2 rad/s
Los momentos de inercia de los discos se calculan mediante la fórmula I=mr2/2, I1=0.5 kg·m2, I2=0.1 kg·m2. Calculamos
-
La velocidad angular de cada uno de los discos en función del tiempo
Los discos alcanzan una velocidad angular constante cuando se cumpla que
ω1·r1=-ω2·r2 (2-0.2·t)·1=-(-0.5·t)·0.5 tf=4.44 s
La velocidad angular final de los discos es
ω1f=2-0.2·4.44=1.11 rad/s
ω2f=-0.5·4.44=-2.22 rad/s
-
El ángulo girado por el primer disco hasta el instante tf =4.44 s es
El ángulo girado por el segundo disco hasta dicho instante es
-
Los momentos angulares inicial y final son
Li=I1·ω0=0.5·2=1 kgm2/s
Lf=I1ω1f+I2·ω2f=0.5·1.11+0.1·(-2.22)=0.33 kgm2/sLa variación de momento angular es
ΔL=Lf-Li=0.33-1=-0.67 kgm2/s
-
El momento de las fuerzas exteriores es
Mext= -F·(r1+r2)=-0.1(1+0.5)=-0.15 N·m
-
El impulso angular es
Mext·tf=-0.15·4.44=-0.67 kgm2/s
El impulso angular de las fuerzas exteriores es igual a la variación del momento angular.
-
La energía cinética inicial es
La energía cinética final es
La variación de energía es
ΔE=Ef-Ei=-0.44 J
-
El trabajo realizado por las fuerzas de rozamiento en el punto de contacto es
El trabajo de dichas fuerzas es igual a la variación de la energía cinética del sistema formado por los dos discos.
Ejemplo 2:
-
Radios de los discos r1=1.0 m, r2=1.0 m
-
Masas de los discos m1=1.0 kg, m2=1.0 kg
-
Fuerza de rozamiento entre las superficies en contacto, F=0.1 N
-
Velocidad angular inicial del disco izquierdo, ω0=2 rad/s
Los momentos de inercia de los discos se calculan mediante la fórmula I=mr2/2, I1=0.5 kg·m2, I2=0.5 kg·m2. Calculamos
-
La velocidad angular de cada uno de los discos en función del tiempo
ω1=2-0.2·t
ω2=-0.2·tLos discos alcanzan una velocidad angular constante cuando se cumpla que
ω1·r1=-ω2·r2 (2-0.2·t)·1=-(-0.2·t)·1 tf=5 s
La velocidad angular final de los discos es
ω1f=2-0.2·5=1 rad/s
ω2f=-0.2·5=-1 rad/s
-
Los ángulos girados por los discos hasta el instante tf =5 s son
θ1f=7.5 rad
θ2f=-2.5 rad
-
Los momentos angulares inicial y final son
Li=I1·ω0=0.5·2=1 kgm2/s
Lf=I1ω1f+I2·ω2f=0.5·1+0.5·(-1)=0 kgm2/sLa variación de momento angular es
ΔL=Lf-Li=0-1=-1 kgm2/s
-
El momento de las fuerzas exteriores es
Mext= -F·(r1+r2)=-0.1(1+1)=-0.2 N·m
-
El impulso angular es
Mext·tf=-0.2·5=-1 kgm2/s
El impulso angular de las fuerzas exteriores es igual a la variación del momento angular.
-
Las energías cinéticas inicial y final
Ei= 1 J
Ef=0.5 JLa variación de energía es
ΔE=Ef-Ei=-0.5 J
-
El trabajo realizado por las fuerzas de rozamiento en el punto de contacto es
El trabajo de dichas fuerzas es igual a la variación de la energía cinética del sistema formado por los dos discos.
Actividades
Se introduce
-
El radio r1 del disco izquierdo (en cm), en el control de edición titulado Radio izquierdo.
-
El radio r2 del disco derecho (en cm), en el control de edición titulado Radio derecho.
-
La masa m1 del disco izquierdo se ha fijado en 1 kg
-
La masa m2 del disco derecho (en kg), en el control de edición titulado Masa derecha
-
La velocidad angular inicial de rotación ω0 (en rad/s), en el control de edición titulado V. angular.
-
La fuerza de rozamiento F (en N), cuando los bordes de los discos deslizan al entrar en contacto.
Se pulsa el botón titulado Inicio
Observamos que el disco izquierdo empieza a girar alrededor de su eje, el disco derecho permanece en reposo.
Se pulsa el botón titulado Empieza.
Los bordes de ambos discos entran en contacto, actúa la fuerza de rozamiento F, disminuyendo la velocidad angular de rotación del primer disco y aumentando la del segundo. Al cabo de cierto tiempo tf los discos giran con velocidades angulares constantes ω1f y ω2f.
A la izquierda del applet, se representa, dos barras verticales de color.
En la primera, se efectúa el balance energético.
-
la energía del disco de la izquierda (en color rojo)
-
la del disco de la derecha (en color azul).
La energía total del sistema formado por los dos discos, vemos que disminuye hasta que se alcanza un valor constante en el instante tf.
La segunda barra representa el momento angular
-
el momento angular del disco izquierdo (en color rojo), su signo es positivo
-
el momento angular del disco derecho (en color azul), su signo es negativo
El momento angular total es la diferencia entre las longitudes de la barra de color rojo y de color azul. Como podemos comprobar el momento angular disminuye hasta el instante tf a partir del cual permanece constante.
Referencias
Robinson W, Watson B. A misuse of angular momentum conservation. Am. J. Phys. 53 (1) January 1985. pp. 82-83
