Medida del módulo de cizallamiento

torsion3.gif (6930 bytes) En una página previa, hemos medido el módulo de elasticidad Y de un material, es decir, la respuesta del material cuando sobre él actúa una fuerza que cambia su volumen (aumentando su longitud). Ahora, examinaremos la deformación por cizallamiento en el que no hay cambio de volumen pero si de forma. El módulo de cizalla G es característico de cada material.

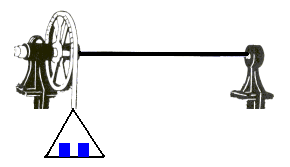
El dispositivo experimental consta de una varilla de un determinado material cuyo radio y longitud se puede modificar. La varilla se mantiene fija por un extremo y por el otro se conecta al eje de una polea de 7 cm radio que puede girar. Se ata una cuerda a la polea y por su extremo libre se van colgando pesas. Por medio de una escala angular se mide el ángulo θ girado para cada momento M aplicado

Módulo de cizalla

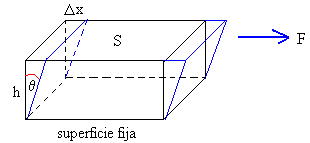Sea un cuerpo en forma de paralepípedo de base S y de altura h.

Cuando la fuerza F que actúa sobre el cuerpo es paralela a una de las caras mientras que la otra cara permanece fija, se presenta otro tipo de deformación denominada de cizallamiento en el que no hay cambio de volumen pero si de forma. Si originalmente la sección transversal del cuerpo tiene forma rectangular, bajo un esfuerzo cortante se convierte en un paralelogramo.

Definimos el esfuerzo como F/S la razón entre la fuerza tangencial al área S de la cara sobre la que se aplica. La deformación por cizalla, se define como la razón Δx/h, donde Δx es la distancia horizontal que se desplaza la cara sobre la que se aplica la fuerza y h la altura del cuerpo, tal como vemos en la figura. El módulo de cizalla G es una propiedad mecánica de cada material

Siendo pequeños los ángulos de desplazamiento podemos escribir

$θ \approx \tan θ = \frac{Δ x}{h}$

$G = \frac{esfuerzo}{deformación} = \frac{F / S}{Δ x / h} = \frac{F / S}{θ}$

Metal	Módulo de cizalla G en 10⁹ N/m²
Cobre estirado en frío	48.0
Aluminio	25.0-26.0
Acero al carbono	8
Acero aleado	80.0
Cinc laminado	31.0
Latón estirado en frío	34.0-36.0
Latón naval laminado	36.0
Bronce de aluminio	41.0
Titanio	44.0
Níquel	79.0
Plata	30.3

Fuente: Koshkin N. I., Shirkévich M.G.. Manual de Física. Editorial Mir (1975)

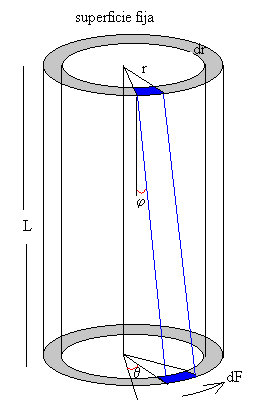torsion2.gif (5305 bytes) Sea una barra de material de forma cilíndrica de radio R y longitud L. Un extremo está fijo, y en el extremo libre se le aplica una fuerza con el fin de producir cizallamiento en la barra cilíndrica. Como vemos en la figura, el rectángulo formado por el eje y el radio del cilindro se ha convertido en un paralelogramo tal como indican las líneas de color azul, φ es el ángulo de deformación.

Una fuerza dF está aplicada paralelamente a la superficie en forma de anillo (en color gris) de radio r y de espesor dr, cuya área es 2π r·dr

El módulo de cizalla es el cociente entre el esfuerzo (fuerza dividido área del anillo) y deformación angular φ

$G = \frac{\frac{d F}{2 π r \cdot d r}}{ϕ}$

Como podemos ver en la figura la relación entre el ángulo φ de deformación y el ángulo θ de desplazamiento angular en el extremo libre es Lφ =rθ .

El momento de la fuerza aplicada es

$M = \int_{0}^{R} r \cdot d F = \int_{0}^{R} \frac{2 π G θ}{L} r^{3} d r = \frac{π G R^{4}}{2 L} θ$

El momento de la fuerza aplicada M es proporcional al ángulo de giro θ del extremo libre

Esta es la fórmula que nos va a permitir medir el módulo de cizalla G, conociendo la longitud L y el radio R de la barra cilíndrica.

Ejemplo:

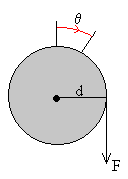torsion4.gif (1679 bytes) Sea una varilla de aluminio

de L=100 cm ó 1.0 m de longitud
de R=3.2 mm ó 0.0032 m de radio.
Colgamos del extremo de la cuerda que pasa por la polea, un peso de 1250 g, el ángulo girado es de 11.9 grados. Con estos datos podemos calcular el módulo de cizalla G.
El momento de la fuerza aplicada es M=F·d=1.25·9.8·0.07=0.8575 N·m

El ángulo girado en radianes es θ =11.9·π /180=0.208 rad

$G = \frac{2 \cdot 0.8575 \cdot 1.0}{π \cdot 0.208 \cdot {(0.0032)}^{4}} = 25.1 \cdot 10^{9} \frac{N}{m^{2}}$

Actividades

Se introduce

La longitud de la varilla en cm
El radio de la varilla en mm
El material del que está hecho la varilla
El radio de la polea se ha fijado en d=7 cm
Se elige el tipo de pesa de 100 g, 250 g ó de 500 g activando el botón de radio correspondiente

Se pulsa el botón titulado Nuevo.

Se arrastra con el puntero del ratón la pesa seleccionada hasta colgarla en el extremo libre de la cuerda.
Se mide el ángulo girado en la escala angular graduada en grados
Se coge otra pesa y se engancha por debajo de la pesa anteriormente colocada.

En el control área de texto, situado a la izquierda del applet se van recogiendo los pares de datos (masa en kg, ángulo girado en grados). Cuando ya se han recogido suficientes datos se pulsa el botón titulado Gráfica. Se representan los datos "experimentales" y la recta que pasa por dichos puntos.

El programa interactivo muestra el valor la pendiente de la recta en grados/kg, en la parte superior del applet. Calculamos el módulo G a partir de la pendiente a de la recta y de los datos de la barra.

Ejemplo:

Barra de aluminio
Longitud L=1.0 m
Radio de la sección de la barra R=0.0032 m
Radio de la polea d=7 cm=0.07 m
Aceleración de la gravedad g=9.8 m/s²

$G = \frac{2 L}{π R^{4}} \frac{M}{θ} = \frac{2 L}{π R^{4}} \frac{F \cdot d}{θ} = \frac{2 L}{π R^{4}} \frac{m g \cdot d}{\frac{θ \cdot π}{180}} = \frac{2 L}{π R^{4}} \frac{g \cdot d \cdot 180}{π} (\frac{m}{θ}) = \frac{2 L}{π R^{4}} \frac{g \cdot d \cdot 180}{π} \frac{1}{a}$

Si la pendiente de la recta es a=9.55 (grados/kg) el valor de G=25.0·10⁹ N/m²

Una vez realizada la "experiencia" se pulsa el botón titulado Respuesta, para comparar el valor del módulo G calculado con el del material seleccionado.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Arrastre la pesa con el puntero del ratón y cuélguela del extremo de la cuerda