• Inicio
• Sólido rígido
• Movimiento general

 Movimiento oscilatorio de un carrete que rueda

Podemos hacer que el carrete describa un movimiento oscilatorio si logramos, mediante algún dispositivo que la fuerza F  forme un ángulo θ  con la horizontal tal que

• θ >θ _c para que el carrete se desplace hacia la izquierda
• θ <θ _c para que el carrete se desplace hacia la derecha
• θ =θ _c el carrete se encuentre en situación de equilibrio

Este dispositivo representado en la figura, es el que se ha simulado en el applet. La parte más difícil es conseguir una fuerza F constante que cambie de dirección a medida que se desplaza el carrete.

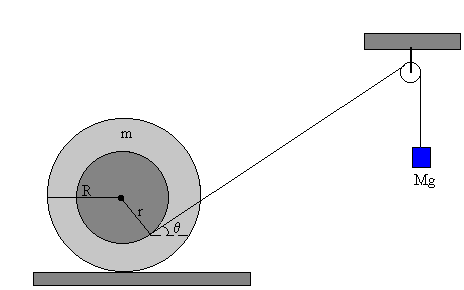
La tensión del hilo es F=Mg-Ma. Como vemos F no es constante ya que depende de la aceleración a del bloque de masa M que cuelga del hilo y que a su vez está relacionada con la aceleración del carrete. En el artículo mencionado en la referencia, se supone que F es aproximadamente constante y apunta hacia un punto fijo.

Posición del carrete

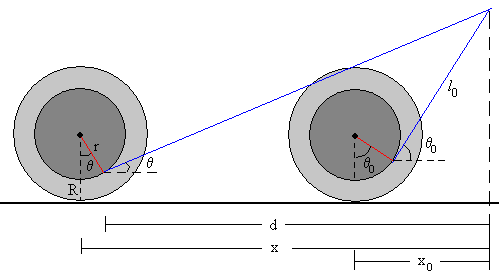
En la parte derecha de la figura, se muestra la posición inicial del carrete

• x₀ es la posición del centro del carrete

• θ₀ es el ángulo que forma la cuerda con la dirección horizontal

• l₀ es la longitud de la cuerda hasta la polea

En la parte izquierda de la figura, se muestra la posición del carrete en el instante t

• x es la posición del centro del carrete

• θ es el ángulo que forma la cuerda con la dirección horizontal

x=-r·sinθ-d

${\displaystyle \tan \theta =\frac{l_0\text{sin}{\theta }_0-r·\cos {\theta }_0+r·\cos \theta }{d}}$

Eliminado la variable auxiliar d

${\displaystyle \tan \theta =\frac{l_0\text{sin}{\theta }_0-r·\cos {\theta }_0+r·\cos \theta }{d}}$

Energía cinética del carrete

El desplazamiento infinitesimal dx que necesitaremos más adelante vale

${\displaystyle dx=\left(\frac{l_0\text{sin}{\theta }_0+r(\cos \theta -\cos {\theta }_0)}{{\text{sin}}^2\theta }\right)d\theta }$

Aplicamos el teorema trabajo-energía. El trabajo de la resultante de las fuerzas que actúa sobre una partícula modifica la energía cinética de dicha partícula.

Si el carrete parte de la posición inicial x₀ con velocidad inicial nula, la energía cinética del carrete de forma cilíndrica cuando su c.m. se encuentra en la posición x es

${\displaystyle \begin{array}{l}{E}_k(x)={\displaystyle \underset{x_0}{\overset{x}{\int }}m{a}_{c}dx}={\displaystyle \underset{x_0}{\overset{x}{\int }}\frac{2}{3}F\left(\cos \theta -\frac{r}{R}\right)dx=}\\ \frac{2}{3}F{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\left(\cos \varphi -\frac{r}{R}\right)\left(\frac{l_0\text{sin}{\theta }_0-r\cos {\theta }_0+r\cos \varphi }{{\text{sin}}^2\varphi }\right)}d\varphi =\\ \frac{2}{3}F{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\left(\left(l_0\text{sin}{\theta }_0-r\cos {\theta }_0-\frac{r^2}{R}\right)\frac{\cos \varphi }{{\text{sin}}^2\varphi }+\left(r-\frac{r}{R}(l_0\text{sin}{\theta }_0-r\cos {\theta }_0)\right)\frac{1}{{\text{sin}}^2\varphi }-r\right)}d\varphi =\\ \frac{2}{3}F{\left(\left(l_0\text{sin}{\theta }_0-r\cos {\theta }_0-\frac{r^2}{R}\right)\frac{-1}{\text{sin}\varphi }+\left(r-\frac{r}{R}(l_0\text{sin}{\theta }_0-r\cos {\theta }_0)\right)\frac{-1}{\tan \varphi }-r\varphi \right]}_{{\theta }_0}^{\theta }=\\ \frac{2}{3}F{\left(\left(-l_0\text{sin}{\theta }_0+r\cos {\theta }_0+\frac{r^2}{R}\right)\frac{1}{\text{sin}\varphi }+\left(-r+\frac{r}{R}(l_0\text{sin}{\theta }_0-r\cos {\theta }_0)\right)\frac{1}{\tan \varphi }-r\varphi \right]}_{{\theta }_0}^{\theta }\end{array}}$

Así pues, la energía cinética E_k del carrete en una posición x, es igual a la diferencia entre el valor final y el valor inicial de una función f(θ) que depende del ángulo θ que hace la cuerda con la dirección horizontal

${\displaystyle \begin{array}{l}{E}_k(x)=f(\theta )-f({\theta }_0)\\ f(\theta )=\frac{2}{3}F\left\{\left(-l_0\text{sin}{\theta }_0+r\cos {\theta }_0+\frac{r^2}{R}\right)\frac{1}{\text{sin}\theta }+\left(-r+\frac{r}{R}(l_0\text{sin}{\theta }_0-r\cos {\theta }_0)\right)\frac{1}{\tan \theta }-r\theta \right\}\\ x=-\frac{r+(l_0\text{sin}{\theta }_0-r\cos {\theta }_0)\cos \theta }{\text{sin}\theta }\end{array}}$

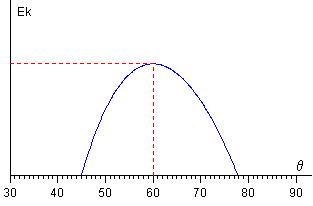
La energía cinética vale cero en la posición d epartida θ₀, alcanza un máximo y se vuelve a valer cero para cierto ángulo θ₁ solución de la ecuación trascendente

f(θ)- f(θ₀)=0

La energía cinética alcanza un valor máximo que se calcula derivando f(θ), es decir, haciendo que el integrando sea cero o bien, que la aceleración a_c sea cero. Esto es, para el ángulo θ_c tal que cosθ_c=r/R, se denomina ángulo crítico

Para representar la figura, se ha tomado r=1.0 y R=2.0. El carrete parte de θ₀=45º alcanza una velocidad máxima para el ángulo crítico θ_c=60º y vuelve a detenerse cuando θ₁ =78º, completando media oscilación. Conocido el dato de la longitud inicial de la cuerda l₀ se puede calcular las posiciones x del centro de masa del carrete para los cuales la velocidad es nula o máxima. En esta descripción, hemos supuesto que no hay fuerzas disipativas y que la energía total se conserva.

Ecuación del movimiento

Ecuación del movimiento

${\displaystyle v=\sqrt{\frac{2E_k}{m}}v=\frac{dx}{dt}=\frac{dx}{d\theta }\frac{d\theta }{dt}}$

Despejando dθ/dt obtenemos una ecuación diferencial de primer orden que resolvemos por procedimientos numéricos con las condiciones iniciales t=0, θ=θ₀

${\displaystyle \frac{d\theta }{dt}=\frac{{\text{sin}}^2\theta }{l_0\text{sin}{\theta }_0+r(\cos \theta -\cos {\theta }_0)}\sqrt{\frac{2\left(f(\theta )-f({\theta }_0)\right)}{m}}}$

Conocido el ángulo θ que forma la cuerda con la dirección horizontal en función del tiempo t, calculamos la posición x del c.m. de carrete en función del tiempo. El carrete presenta un movimiento oscilatorio que difiere del  Movimiento Armónico Simple.

Actividades

Se introduce

• El peso Mg del cuerpo que cuelga, en el control de edición titulado Peso. La tensión F del hilo se supone que es constante e igual a dicho peso.
• El ángulo inicial de partida, actuando en la barra de desplazamiento titulada  Ángulo
• La masa del carrete m=1,
• El radio interior del carrete r=1 y el exterior es R=2.0.La relación de radios es r/R=0.5, el ángulo crítico se mantiene fijo e igual a θ_c=60º.
• La longitud inicial de la cuerda se ha fijado en l₀=20

Se pulsa el botón titulado Empieza

Podemos observar que el movimiento del carrete está descrito cualitativamente por la curva de energía cinética (a la izquierda del applet). Se representa la energía cinética en el intervalo angular en (θ₀, θ₁) en el que se mueve el carrete, o bien desde x₀ a x₁. El carrete parte de θ₀ con velocidad cero o con energía cinética cero, va aumentando hasta alcanzar un máximo en el ángulo crítico θ_c=60º, decelera hasta que alcanza la posición de retorno θ₁, donde la energía cinética vuelve a ser cero. El carrete invierte su dirección y vuelve de nuevo al punto de partida completando una oscilación.

Pulsando el botón titulado Gráfica se representa el ángulo θ , en función del tiempo. Podemos apreciar a simple vista que se trata de un movimiento oscilatorio, pero difiere de un Movimiento Armónico Simple.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Carnero C, Carpena P, Aguiar J. The rolling body paradox: an oscillatory motion approach. Eur. J. Phys. 18 (1997) pp. 409-416

Curso Interactivo de Física en Internet © Ángel Franco García