• Inicio
• Sólido rígido
• Dinámica de rotación

Estática y dinámica de una escalera apoyada en dos paredes perpendiculares.

En esta página, vamos a estudiar el comportamiento de una escalera homogénea apoyada en dos paredes perpendiculares. Supondremos que la pared vertical no ejerce ninguna fuerza de rozamiento sobre el apoyo.

Estática

Supongamos una escalera homogénea de masa m y longitud L apoyada en dos paredes perpendiculares. Las fuerzas sobre la escalera son las que se ha dibujado en la figura.

Fy y Fr son las fuerzas de rozamiento que ejercen las paredes vertical y horizontal en los respectivos apoyos. Fx y N son las reacciones de la pared mg es el peso que actúa en el centro de masas de la escalera supuesta homogénea.

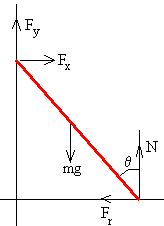La situación de equilibrio solamente nos proporciona tres ecuaciones (dos para las fuerzas y una para los momentos), sin embargo, tenemos cuatro incógnitas, el problema es indeterminado. Véase el primer artículo citado en las referencias.

Para resolver el problema tenemos que suponer por ejemplo que F_y=0, en la pared vertical no hay rozamiento.

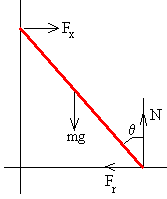Cuando la escalera forma un ángulo θ con la vertical las ecuaciones de equilibrio son:

1. La resultante de la fuerzas debe ser cero.

${\displaystyle \begin{array}{l}{F}_x=F_r\\ N=mg\end{array}}$

2. El momento de las fuerzas respecto de cualquier punto (por ejemplo el extremo inferior de la escalera) es cero.

${\displaystyle -F_{x}L\cos \theta +mg\frac{L}{2}\sin \theta =0}$

Conocido el ángulo θ, despejamos la fuerza de rozamiento F_r que impide que el extremo inferior deslice a lo largo de la pared horizontal

${\displaystyle F_r=\frac{mg}{2}\tan \theta }$

A medida que se incrementa el ángulo θ, se inclina cada vez más la escalera, la fuerza de rozamiento aumenta. Alcanza su valor máximo cuando

F_r=μ_sN= μ_smg

Donde μ_s es el coeficiente estático de rozamiento

El ángulo límite θ_l a partir del cual la escalera empieza a deslizar es

tanθ_l=2μ_s

Dinámica

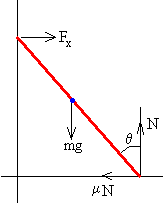
Si el ángulo que forma la escalera es mayor que el límite, θ₀>θ_l la escalera empieza a deslizar. La fuerza de rozamiento F_r=μN en el extremo inferior de la escalera disminuye ligeramente, ya que el coeficiente cinético μ suele ser menor que el estático μ_s

El movimiento de la escalera consta de dos etapas:

1.- El extremo superior de la escalera permanece en contacto con la pared vertical

• Movimiento de traslación del cm.

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=F_x-F_r\\ m\frac{d^{2}y}{d{t}^2}=N-mg\end{array}}$

• Movimiento de rotación alrededor de un eje perpendicular al plano del dibujo que pasa por el centro de masas

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=N\frac{L}{2}\text{sin}\theta -F_x\frac{L}{2}\cos \theta -F_r\frac{L}{2}\cos \theta }$

con  I_c=mL²/12, se supone que la escalera es una varilla homogénea de masa m y longitud L

La posición del centro de masas es (x, y). Mientras el extremo superior de la escalera está apoyado en la pared vertical F_x>0, hay una relación entre x, y y el ángulo θ.

${\displaystyle x=\frac{L}{2}\sin \theta y=\frac{L}{2}\cos \theta }$

Derivamos dos veces respecto del tiempo

${\displaystyle \begin{array}{l}\frac{dx}{dt}=\frac{L}{2}\cos \theta \frac{d\theta }{dt}\\ \frac{d^{2}x}{d{t}^2}=\frac{L}{2}\left\{-\text{sin}\theta {\left(\frac{d\theta }{dt}\right)}^2+\cos \theta \frac{d^2\theta }{d{t}^2}\right\}\\ \frac{dy}{dt}=-\frac{L}{2}\text{sin}\theta \frac{d\theta }{dt}\\ \frac{d^{2}y}{d{t}^2}=-\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

Despejamos F_x y N en las ecuaciones del movimiento del c.m.

${\displaystyle \begin{array}{l}N=mg-m\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\\ F_x=\mu mg+m\frac{L}{2}\left\{\frac{d^2\theta }{d{t}^2}\left(\cos \theta -\mu \text{sin}\theta \right)-{\left(\frac{d\theta }{dt}\right)}^2\left(\text{sin}\theta +\mu \cos \theta \right)\right\}\end{array}}$

Introducimos N, F_x y F_r=μN en la ecuación de la dinámica de rotación.

${\displaystyle \left(I_c+m\frac{L^2}{4}-m\frac{L^2}{2}\mu \text{sin}\theta \cos \theta \right)\frac{d^2\theta }{d{t}^2}=\left(m\frac{L^2}{2}\mu \text{cos}\theta \cos \theta \right){\left(\frac{d\theta }{dt}\right)}^2+mg\frac{L}{2}\text{sin}\theta -mg\frac{L}{2}\mu \cos \theta }$

Se resuelve la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: En el instante t=0, dθ/dt=0, θ=θ₀.

Observamos que la fuerza horizontal que ejerce la pared vertical F_x va disminuyendo hasta que se hace cero en el instante t₁. El ángulo que forma la escalera con la vertical es θ₁  y la velocidad angular de rotación es (dθ/dt)₁. La velocidad horizontal del centro de masas es

${\displaystyle {\left(\frac{dx}{dt}\right)}_1=\frac{L}{2}\cos {\theta }_1{\left(\frac{d\theta }{dt}\right)}_1}$

2.- El extremo superior de la escalera deja de estar en contacto con la pared vertical

 

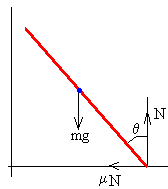
Las ecuaciones del movimiento son

• Movimiento de traslación del centro de masas

${\displaystyle \begin{array}{l}m\frac{d^{2}x}{d{t}^2}=-\mu N\\ m\frac{d^{2}y}{d{t}^2}=N-mg\end{array}}$

• Movimiento de rotación alrededor de un eje que pasa por el centro de masas

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=N\frac{L}{2}\text{sin}\theta -\mu N\frac{L}{2}\cos \theta }$

La ordenada y del centro de masas es

${\displaystyle y=\frac{L}{2}\cos \theta }$

Derivamos dos veces respecto del tiempo

${\displaystyle \begin{array}{l}\frac{dy}{dt}=-\frac{L}{2}\text{sin}\theta \frac{d\theta }{dt}\\ \frac{d^{2}y}{d{t}^2}=-\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\end{array}}$

Despejamos la reacción N

${\displaystyle N=mg-m\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}}$

Introducimos la expresión de N en la ecuación de la dinámica de rotación y en la de traslación del c.m. Obtenemos el sistema de dos ecuaciones diferenciales de segundo orden

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=g-\frac{L}{2}\left\{\cos \theta {\left(\frac{d\theta }{dt}\right)}^2+\text{sin}\theta \frac{d^2\theta }{d{t}^2}\right\}\\ \left(I_c+m\frac{L^2}{4}\text{sin}\theta (\text{sin}\theta -\mu \cos \theta )\right)\frac{d^2\theta }{d{t}^2}=\left(-m\frac{L^2}{4}\text{cos}\theta (\text{sin}\theta -\mu \cos \theta )\right){\left(\frac{d\theta }{dt}\right)}^2+mg\frac{L}{2}(\text{sin}\theta -\mu \cos \theta )\end{array}}$

Se resuelve este sistema de dos ecuaciones diferenciales con las siguientes condiciones iniciales: en el instante t₁, el ángulo que forma la escalera con la vertical es θ₁, la velocidad angular de rotación es (dθ/dt)₁ y la velocidad horizontal del centro de masas es

${\displaystyle {\left(\frac{dx}{dt}\right)}_1=\frac{L}{2}\cos {\theta }_1{\left(\frac{d\theta }{dt}\right)}_1}$

Se detiene el movimiento cuando la escalera forma un ángulo θ=π/2 con la dirección vertical, cuando la escalera está tumbada en el suelo.

Actividades

Se introduce

• El ángulo θ₀ que forma la escalera con la vertical, actuando en la barra de desplazamiento titulada Ángulo

• El coeficiente estático de rozamiento μ_s, actuando en la barra de desplazamiento titulada C. estático.

• El coeficiente cinético de rozamiento μ, actuando en la barra de desplazamiento titulada C. cinético

• Se han fijado la longitud de la escalera en L=10 m y la masa m=10 kg

Se pulsa el botón titulado Empieza

Si el ángulo θ₀ es menor que el ángulo límite tanθ_l=2μ_s

• La escalera permanece en equilibrio

• En caso contrario, observamos el movimiento de la escalera y las fuerzas sobre la misma.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Mendelson K. S. Statics of a ladder leaning against a rough wall. Am. J. Phys. 63 (2) February 1995. pp. 148-150.

Curso Interactivo de Física en Internet © Ángel Franco García