• Inicio
• Sólido rígido
• Dinámica de rotación

Caída de un lápiz en posición vertical

El movimiento de caída de un lápiz nos muestra que la ecuación del movimiento

${\displaystyle \frac{d{L}_0}{dt}=M_0}$

donde el momento angular L y y el momento de las fuerzas exteriores M se evalúan en el punto O de contacto del lápiz con el suelo no es correcta, ya que O no está en reposo con respecto a un sistema inercial de referencia.

Tenemos que usar la ecuación

${\displaystyle \frac{d{L}_{cm}}{dt}=M_{cm}}$

que es válida incluso si el centro de masas (c.m.) no está en reposo con relación al sistema inercial de referencia

Ecuación del movimiento

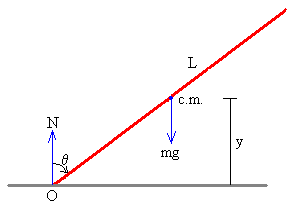Las fuerzas sobre el lápiz son: El peso mg que actúa en el centro de masas La reacción del suelo N que actúa en el punto de contacto

La posición del c.m. es

y=(L/2)cosθ 

La velocidad del c.m. es

${\displaystyle \frac{dy}{dt}=\frac{L}{2}\frac{d\theta }{dt}\text{sin}\theta }$

Ecuación del movimiento del centro de masas

${\displaystyle m\frac{d^{2}y}{d{t}^2}=N-mg}$

que podemos escribir en términos del ángulo θ

${\displaystyle -m\frac{L}{2}\cos \theta {\left(\frac{d\theta }{dt}\right)}^2-m\frac{L}{2}\text{sin}\theta \frac{d^2\theta }{d{t}^2}=N-mg}$     (1)

La ecuación del movimiento de rotación alrededor del c.m. es

${\displaystyle I_c\frac{d^2\theta }{d{t}^2}=N\frac{L}{2}\text{sin}\theta }$       (2)

Donde $I_c=\frac{1}{12}m{L}^2$ es el momento de inercia de una varilla de masa m y longitud L respecto de un eje perpendicular a la varilla que pasa por el c.m.

Eliminando la reacción N de las ecuaciones (1) y (2), obtenemos una ecuación diferencial que se resuelve por procedimientos numéricos

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{\left(\frac{2g}{L}-{\left(\frac{d\theta }{dt}\right)}^2\cos \theta \right)\text{sin}\theta }{\frac{1}{3}+{\text{sin}}^2\theta }}$

con las condiciones iniciales: t=0, θ= θ₀, dθ/dt=0.

Una vez calculado el ángulo θ en el instante t, la altura y del c.m. vale y=(L/2)cosθ.

Aproximación

Cuando el lápiz está en posición casi vertical, el ángulo θ es pequeño, y la velocidad dθ/dt es pequeña, la ecuación diferencial se puede escribir

${\displaystyle \frac{d^2\theta }{d{t}^2}=\frac{6g}{L}\theta }$

La solución de esta ecuación diferencial es de la forma

${\displaystyle \theta =A\exp (-kt)+B\exp (kt)k=\sqrt{\frac{6g}{L}}}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales t=0, θ= θ₀, dθ/dt=0.

θ=θ₀·cosh(k·t)

Si kt es grande, el coseno hiperbólico se puede aproximar a cosh(kt)≈exp(kt)/2, despejamos el tiempo t. 

${\displaystyle t=\sqrt{\frac{L}{6g}}\ln \frac{2\theta }{{\theta }_0}}$

Por ejemplo si L=1 m, θ₀=0.0001 rad y θ=0.1 rad, el tiempo t=0.99 s.

Balance energético

La energía cinética del lápiz es la suma de la energía de cinética de rotación alrededor del c.m. más la energía de traslación del c.m.

${\displaystyle E_k=\frac{1}{2}{I}_c{\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}m{\left(\frac{dy}{dt}\right)}^2=\frac{1}{8}m{L}^2\left(\frac{1}{3}+{\text{sin}}^2\theta \right){\left(\frac{d\theta }{dt}\right)}^2}$

La energía potencial del c.m. es

E_p=mgy=mg(L/2)cosθ

La suma de ambas contribuciones es la energía total, que es la energía potencial inicial del lápiz

${\displaystyle \frac{1}{8}m{L}^2\left(\frac{1}{3}+{\text{sin}}^2\theta \right){\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{2}mgL\cos \theta =\frac{1}{2}mgL\cos {\theta }_0}$

Derivando con respecto del tiempo,

${\displaystyle \frac{1}{8}m{L}^2\left(2\text{sin}\theta \cos \theta \frac{d\theta }{dt}\right){\left(\frac{d\theta }{dt}\right)}^2+\frac{1}{8}m{L}^2\left(\frac{1}{3}+{\text{sin}}^2\theta \right)2\frac{d\theta }{dt}\frac{d^2\theta }{d{t}^2}-\frac{1}{2}mgL\text{sin}\theta \frac{d\theta }{dt}=0}$

despejamos d²θ/dt² y volvemos a obtener de nuevo la ecuación del movimiento.

En la posición final θ=π/2, la energía potencial del c.m. es nula, y la energía cinética se reparte del siguiente modo:

• una cuata parte para la energía cinética de rotación

• tres cuartas partes para la de traslación del c.m.

Actividades

Se introduce

• El ángulo θ₀ que forma el lápiz con la vertical en el instante inicial t=0, actuando en la barra de desplazamiento titulada Ángulo

• La masa de la barra se ha fijado en m=1 kg

• La longitud de la barra se ha fijado en L=1 m

Se pulsa el botón titulado Empieza

Observamos el movimiento del lápiz. En la parte derecha, tenemos un diagrama que nos muestra como van cambiando los distintos tipos de energía a medida que cae el lápiz

• la energía potencial, en color azul

• la energía cinética de rotación, en color rosa

• la energía cinética de traslación del c.m,. en color rojo

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Crawford F. S. Problem: Moments to remember. Am. J. Phys. 57 (2) February 1989, pp. 105, solución 177

Curso Interactivo de Física en Internet © Ángel Franco García