Raíces de una ecuación |
Cálculo de los coeficientes en las sucesivas iteracciones
En muchos campos de las matemáticas es necesario hallar las raíces de un polinomio, por ejemplo, para calcular la integral de una función racional, en la transformada de Laplace, etc. Solamente existen fórmulas si el polinomio tiene un grado igual o inferior a cuatro. Excepto para los polinomios de primer y segundo grado, las fórmulas son complicadas, por lo que se emplean procesos de aproximación numérica. Entre los numerosos métodos que existen, el más conocido es quizá el método de Newton. Sin embargo, describiremos un método, realmente ingenioso, que nos proporciona gran exactitud en las raíces de un polinomio.
Sea el polinomio
![]() (1)
(1)
Hacemos el polinomio más simple dividiendo todos los coeficientes por el primer término de modo que a0 es siempre 1. Supongamos que sus raíces reales y distintas son
![]()
Al elevar al cuadrado el polinomio y agrupar los términos se obtiene un polinomio de grado 2n
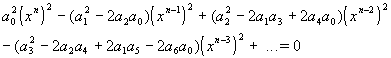 (2)
(2)
Cuyas raíces serán
![]()
Hemos construido así una nueva ecuación cuyas raíces son numéricamente iguales a los cuadrados de las raíces de la ecuación original. Repitiendo el proceso, se pueden obtener ecuaciones cuyas raíces sean numéricamente iguales a las potencias cuarta, octava, decimosexta, etc. de las raíces de la ecuación original. El efecto de este proceso de elevar al cuadrado es el de producir ecuaciones cuyas raíces están cada vez más separadas. Por ejemplo, si dos raíces de la ecuación original están entre sí como 5 : 4 sus potencias 128 están en la razón 5128 : 4128, o sea, 2.54 1012: 1, lo que es muy deseable ya que las ecuaciones cuyas raíces están muy separadas se pueden resolver rápidamente con exactitud considerable. Supóngase ahora, que reiterando el proceso de elevación al cuadrado se llega a un polinomio
![]() (3)
(3)
donde m es el número de veces que se repite el proceso de elevación al cuadrado. Así, si se repite siete veces el proceso de elevación al cuadrado, 2m =27 =128 sería el exponente al que estarían elevados las sucesivas potencias xn, xn-1, xn-2, ... del polinomio. Sus raíces serán las del polinomio original elevadas al exponente 2m.
![]()
Por las relaciones conocidas entre raíces y coeficientes del polinomio, se tiene que
![]()
![]()
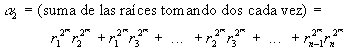
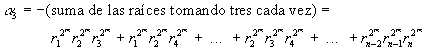

En la suposición de que
![]()
y de que 2m es grande por ejemplo 128 o 256, se cumplirá que
![]()
donde el símbolo >>> indica mucho mayor que. Las relaciones entre coeficientes y raíces quedarán simplificadas con gran aproximación a las expresiones.
![]()
![]()
![]()
![]()
![]()
Así, el módulo de r1 se puede hallar extrayendo la raíz 2m-ésima de a1 . De la segunda ecuación se obtiene r2, y así sucesivamente. La fórmula para obtener el módulo de la raíz ri es
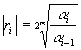
En la práctica, hallamos el logaritmo de ri, y luego, calculamos el antilogaritmo del resultado obtenido, de este modo se obtiene el valor absoluto de la raíz ri.
![]() (4)
(4)
Para determinar el signo, se halla el valor del polinomio original para los valores ri, y -ri, uno de los dos hará que dicho valor sea próximo a cero, y por tanto, será la raíz buscada.
Un polinomio cuyas raíces son reales y distintas es el caso más simple que se nos
puede presentar. Sea por ejemplo el polinomio
![]() ,cuyas
raíces como se puede comprobar fácilmente por simple sustitución son 3, 2, y -1. En la
tabla se observa los coeficientes ai
resultantes del proceso de elevación del polinomio a las potencias 2, 4, 8, 16, 32, 64,
128, 256 y 512 respectivamente.
,cuyas
raíces como se puede comprobar fácilmente por simple sustitución son 3, 2, y -1. En la
tabla se observa los coeficientes ai
resultantes del proceso de elevación del polinomio a las potencias 2, 4, 8, 16, 32, 64,
128, 256 y 512 respectivamente.
| m (2m) | a0 | a1 | a2 | a3 |
| 0 (1) | 1.0 | -4.0 | 1.0 | 6.0 |
| 1 (2) | 1.0 | 14.0 | 49.0 | 36.0 |
| 2 (4) | 1.0 | 98.0 | 1393.0 | 1296.0 |
| 3 (8) | 1.0 | 6818.0 | 1.6864 106 | 1.6796 106 |
| 4 (16) | 1.0 | 4.3112 107 | 2.8212 1012 | 2.8211 1012 |
| 5 (32) | 1.0 | 1.8553 1015 | 7.9587 1024 | 7.9587 1024 |
| 6 (64) | 1.0 | 3.4337 1030 | 6.334 1049 | 6.334 1049 |
| 7 (128) | 1.0 | 1.179 1061 | 4.012 1099 | 4.012 1099 |
| 8 (256) | 1.0 | 1.3901 10122 | 1.6096 10199 | 1.6096 10199 |
| 9 (512) | 1.0 | 1.9323 10244 | 2.5908 10398 | 2.5908 10398 |
Podemos observar en la tabla que cada coeficiente en la iteración 9, es aproximadamente el cuadrado del coeficiente en la iteración precedente, habiéndose eliminado el efecto de los dobles productos
A partir de este ejemplo, tenemos que codificar el procedimiento de Graeffe cualquiera que sea el grado n del polinomio y el número m de veces que se repite el proceso de elevación al cuadrado, lo que requiere los siguientes pasos:
Reservamos memoria para un array bidimensional a, y guardamos en la primera fila los coeficientes del polinomio, de mayor a menor grado.
a= new double[MAX_ITER][n+1];
//la primera fila de la tabla guarda los coeficientes del polinomio
for(int j=0; j<n+1; j++){
a[0][j]=coef[j];
}
for(int m=1; m<MAX_ITER; m++){
for(int j=0; j<n+1; j++){
a[m][j]=0.0;
}
}
Donde MAX_ITER es el número máximo de iteracciones, o de veces que se repite el proceso de elevación al cuadrado.
En una función miembro denominada tabla, codificaremos el procedimiento de elevación al cuadrado de un polinomio de grado n. Partiendo del polinomio original (1), obtenemos el polinomio resultante del procedimiento de elevar al cuadrado (3) según el esquema (2). En la expresión (2) observamos que el coeficiente de grado i del nuevo polinomio ai se obtiene efectuando las siguientes operaciones entre los coeficientes del polinomio original: se calcula el cuadrado de ai y se halla el doble producto de los elementos equidistantes ak y al, siendo los índices k=i-s y l=i+s, con s=1, 2, 3... hasta que se llegue al final del polinomio. Por ejemplo, los elementos equidistantes a a3 en un polinomio de 6º grado son (a2, a4), (a1, a5) y (a0, a6). Por tanto, el nuevo coeficiente ai del polinomio elevado al cuadrado se calculará mediante la fórmula
![]()
Sorprendentemente, el lenguaje Java, no produce error por "overflow", es decir, cuando se supera el límite máximo o mínimo para un tipo de dato básico: int, long, o double. Por ejemplo, podemos guardar números enteros en una variable tipo int siempre que esté en el intervalo -2147483648 a 2147483647. Las clases que envuelven a los tipos primitivos de datos, Integer, Double, etc. nos proporcionan funciones miembro que nos notifican cuando se sobrepasen los límites especificados para un tipo de dato dado.
En el código de la función tabla, cuando se supera el valor máximo que puede guardar un dato de tipo double, se interrumpe el proceso de elevación al cuadrado, y se sale fuera del bucle. La función estática isInfinite de la clase Double se encarga de verificarlo devolviendo true si hemos superado dicho límite permitido.
exterior:
do{
for(int i=0; i<n+1; i++){
a[m][i]=a[m-1][i]*a[m-1][i];
if(Double.isInfinite(a[m][i])){
break exterior;
}
}
//....
m++;
}while(m<MAX_ITER);
Es necesario emplear un break con una etiqueta para salir al bucle exterior do...while, e interumpir el proceso de elevación al cuadrado. Si solamente empleamos break salimos del bucle interior for y se continuaría en el bucle do...while el proceso de cálculo.
Nos queda ahora, la determinación el signo de cada uno de los dobles productos. Si el índice s es impar, entonces el signo es negativo, y si es par el signo es positivo. En vez de elevar -1 a la potencia s, empleamos el operador módulo % en conjunción con la macro if ... else, que se leerá: si s es impar (el resto de dividir s entre 2 es cero), entonces el valor de la variable entera signo es +1 en caso contrario es -1.
signo=(s%2==0)? +1: -1;
Los coeficientes del polinomio original se guarda en el array a[0][i], (i=0 ... n). Cuando se eleva al cuadrado los coeficientes del nuevo polinomio se guardan en el array a[1][i], (i=0 ... n), y así sucesivamente. Los coeficientes a[m][i], (i=0 ... n) corresponden al polinomio que se ha elevado a la potencia 2m. Dicha potencia se calcula mediante un bucle for.
pot2=1;
for(int i=1; i<=m; i++){
pot2*=2;
}
El código de la función tabla, que calcula los coeficientes polinomio resultante del proceso de elevar el polinomio original sucesivamente al cuadrado m veces, es el siguiente
private void tabla(){
int k,l, signo;
//divide el polinomio por el primer coeficiente, las raíces no cambian
for(int i=1; i<n+1; i++){
a[0][i]/=a[0][0];
}
a[0][0]=1.0;
m=1;
exterior: //etiqueta
do{
//cuadrados
for(int i=0; i<n+1; i++){
a[m][i]=a[m-1][i]*a[m-1][i];
if(Double.isInfinite(a[m][i])){
break exterior;
}
}
//dobles productos
for(int i=1; i<n; i++){
for(int s=1; s<n/2+1; s++){
k=i-s; l=i+s;
if((k<0)||(l>n)) break; //términos simétricos
signo=(s%2==0)? +1: -1;
a[m][i]+=signo*2*a[m-1][k]*a[m-1][l];
if(Double.isInfinite(a[m][i])){
break exterior;
}
}
}
m++;
}while(m<MAX_ITER);
m--;
//potencia de m de 2
pot2=1;
for(int i=1; i<=m; i++){
pot2*=2;
}
}
|