Raíces de una ecuación |
Una raíz compleja y su conjugada
Dos raíces complejas y sus conjugadas
Un polinomio cuyas raíces son reales y distintas es el caso más simple que se nos
puede presentar. Volvemos a estudiar el polinomio
![]() ,
cuyas raíces como se puede comprobar fácilmente por simple sustitución son 3, 2, y -1.
Creamos la tabla de
las sucesivas potencias
,
cuyas raíces como se puede comprobar fácilmente por simple sustitución son 3, 2, y -1.
Creamos la tabla de
las sucesivas potencias
| m (2m) | a0 | a1 | a2 | a3 |
| 0 (1) | 1.0 | -4.0 | 1.0 | 6.0 |
| 1 (2) | 1.0 | 14.0 | 49.0 | 36.0 |
| 2 (4) | 1.0 | 98.0 | 1393.0 | 1296.0 |
| 3 (8) | 1.0 | 6818.0 | 1.6864 106 | 1.6796 106 |
| 4 (16) | 1.0 | 4.3112 107 | 2.8212 1012 | 2.8211 1012 |
| 5 (32) | 1.0 | 1.8553 1015 | 7.9587 1024 | 7.9587 1024 |
| 6 (64) | 1.0 | 3.4337 1030 | 6.334 1049 | 6.334 1049 |
| 7 (128) | 1.0 | 1.179 1061 | 4.012 1099 | 4.012 1099 |
| 8 (256) | 1.0 | 1.3901 10122 | 1.6096 10199 | 1.6096 10199 |
| 9 (512) | 1.0 | 1.9323 10244 | 2.5908 10398 | 2.5908 10398 |
Los módulos de las raíces reales, se calculan mediante la fórmula (4). Para hallar las raíces con gran exactitud tomaremos los coeficientes que figuran en la última fila, resultado de elevar el polinomio a la potencia 512.
log r0=(log(
a1)-log(a0))/2m
log r1=(log(a2)-log(a1))/2m
log r1=(log(2.5908 10398)-log(1.9323 10244))/512
r1 sale 2
log r2=(log(a3)-log(a2))/2m
log r2=(log(2.5908 10398)-log(2.5908 10398))/512
r2 sale 1
Para codificar estos cálculos, emplearemos las funciones exponencial y logarítmica: Math.log que halla el logaritmo de la raíz, y la función recíproca Math.exp, para hallar la raíz. El valor absoluto de la raíz real se guarda en la variable local raiz.
private void raizRealSimple(int j){
//valor absoluto de la raíz
double logaritmo=(Math.log(a[m][j])-Math.log(a[m][j-1]))/pot2;
double raiz=Math.exp(logaritmo);
//determinación del signo
raicesReales[numReales]=(Math.abs(valorPolinomio(raiz))<Math.abs(valorPolinomio(-raiz)))? raiz : -raiz;
numReales++;
}
|
Para determinar el signo de la raíz real, hallaremos el valor del polinomio para dos valores raiz y -raiz, uno de los dos tiene que ser cero o muy próximo a cero. Una vez hallada la raíz real, su valor absoluto y su signo, se guarda en el array raicesReales.
En el apartado anterior, hemos supuesto que las raíces de un polinomio son reales y
distintas, por lo que la aplicación del método de Graeffe es inmediata. Supongamos el
polinomio ![]() que tiene una raíz doble 2, y una simple
3. Examinemos el comportamiento de sus coeficientes en el proceso de elevación al
cuadrado en la tabla. Observaremos que el segundo coeficiente a1
se comporta como hemos descrito en el apartado anterior, cada coeficiente en una
iteración es aproximadamente el cuadrado de la iteración precedente. Sin embargo, este
comportamiento no se produce en el tercer coeficiente a2,
ya que se obtiene la mitad del valor esperado. Por ejemplo, el valor de a2 en la séptima iteración es 8.024 1099
y su cuadrado es 6.4384 10199, sin embargo, se obtiene la mitad 3.2192 10199.
Lo mismo ocurre en octava iteración el cuadrado de 3.2192 10199
es 1.0363 10399, sin embargo, obtenemos la mitad de este valor 5.1817 10398.
Al tercer coeficiente, a2 (índice
2), se denomina excepcional, y señala la presencia de raíces reales dobles.
que tiene una raíz doble 2, y una simple
3. Examinemos el comportamiento de sus coeficientes en el proceso de elevación al
cuadrado en la tabla. Observaremos que el segundo coeficiente a1
se comporta como hemos descrito en el apartado anterior, cada coeficiente en una
iteración es aproximadamente el cuadrado de la iteración precedente. Sin embargo, este
comportamiento no se produce en el tercer coeficiente a2,
ya que se obtiene la mitad del valor esperado. Por ejemplo, el valor de a2 en la séptima iteración es 8.024 1099
y su cuadrado es 6.4384 10199, sin embargo, se obtiene la mitad 3.2192 10199.
Lo mismo ocurre en octava iteración el cuadrado de 3.2192 10199
es 1.0363 10399, sin embargo, obtenemos la mitad de este valor 5.1817 10398.
Al tercer coeficiente, a2 (índice
2), se denomina excepcional, y señala la presencia de raíces reales dobles.
| m (2m) | a0 | a1 | a2 | a3 |
| 0 (1) | 1.0 | -7.0 | 16.0 | -12.0 |
| 1 (2) | 1.0 | 17.0 | 88.0 | 144.0 |
| 2 (4) | 1.0 | 113.0 | 2048.0 | 20736.0 |
| 3 (8) | 1.0 | 7073.0 | 3.4248 106 | 4.2998 108 |
| 4 (16) | 1.0 | 4.3178 107 | 5.6465 1012 | 1.8488 1017 |
| 5 (32) | 1.0 | 1.853 1015 | 1.5917 1025 | 3.4182 1034 |
| 6 (64) | 1.0 | 3.4337 1030 | 1.2668 1050 | 1.1684 1069 |
| 7 (128) | 1.0 | 1.179 1061 | 8.024 1099 | 1.3652 10138 |
| 8 (256) | 1.0 | 1.3901 10122 | 3.2192 10199 | 1.8638 10276 |
| 9 (512) | 1.0 | 1.9323 10244 | 5.1817 10398 | 3.4737 10552 |
Para obtener la raíz doble, se ha de aplicar la siguiente fórmula que damos sin justificar. La raíz repetida se puede hallar calculando la raíz 2*2m de la razón de los coeficientes que inmediatamente preceden y siguen al coeficiente excepcional. Si i es el coeficiente excepcional, el módulo de la raíz doble se calcula mediante la fórmula
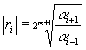 (5)
(5)
La codificación de la función raizRealDoble es similar a la función raizRealSimple. Primero, halla el módulo de la raíz aplicando la fórmula (5), y posteriormente, determina su signo. La raíz buscada se guarda dos veces en el array raicesReales, y se incrementa dos unidades el contador de raíces reales numReales.
private void raizRealDoble(int j){
//valor absoluto de la raíz
double logaritmo=(Math.log(a[m][j+1])-Math.log(a[m][j-1]))/(2*pot2);
double raiz=Math.exp(logaritmo);
//determinación del signo
boolean bPositiva=false, bNegativa=false;
if (Math.abs(valorPolinomio(raiz))<CERO){
raicesReales[numReales]=raiz;
numReales++;
bPositiva=true;
}
if (Math.abs(valorPolinomio(-raiz))<CERO){
raicesReales[numReales]=-raiz;
numReales++;
bNegativa=true;
}
if(bPositiva && !bNegativa){
raicesReales[numReales]=raiz;
numReales++;
}
if(!bPositiva && bNegativa){
raicesReales[numReales]=-raiz;
numReales++;
}
}
|
Los polinomios pueden tener también raíces complejas, y sus respectivas conjugadas.
El caso más simple es el del un polinomio x2+1 que tiene una raíz compleja y
su correspondiente conjugada. Sea el polinomio ![]() que tiene las siguientes raíces exactas: 3, 2-3i, 2+3i.
que tiene las siguientes raíces exactas: 3, 2-3i, 2+3i.
Examinando en la tabla los valores y los signos de los coeficientes en las sucesivas iteraciones, vemos que el segundo coeficiente a1 cambia de signo en la tercera iteración, además el valor del coeficiente en una iteración no es aproximadamente igual al cuadrado de su valor en la siguiente iteración, sino la mitad de dicho valor, un comportamiento similar al de las raíces dobles. Al coeficiente a1 le denominaremos coeficiente excepcional.
| m (2m) | a0 | a1 | a2 | a3 |
| 0 (1) | 1.0 | -7.0 | 25.0 | -39.0 |
| 1 (2) | 1.0 | -1.0 | 79.0 | 1521.0 |
| 2 (4) | 1.0 | -157.0 | 9283.0 | 2.3134 106 |
| 3 (8) | 1.0 | 6083.0 | 8.1259 108 | 5.352 1012 |
| 4 (16) | 1.0 | -1.5882 109 | 5.952 1017 | 2.8644 1025 |
| 5 (32) | 1.0 | 1.3319 1018 | 4.4524 1035 | 8.2048 1050 |
| 6 (64) | 1.0 | 8.8358 1035 | 1.9606 1071 | 6.7319 10101 |
| 7 (128) | 1.0 | 3.886 1071 | 3.8437 10142 | 4.5318 10203 |
| 8 (256) | 1.0 | 7.4134 10142 | 1.4774 10285 | 2.0537 10407 |
| 9 (512) | 1.0 | 2.5411 10285 | 2.1827 10570 | 4.2177 10814 |
Para conocer si un polinomio tiene raíces complejas y sus correspondientes conjugadas basta examinar el cambio de signo de los coeficientes en sucesivas iteraciones, a partir, por ejemplo, de la segunda. Para ello, declaramos y definimos una función miembro denominada cambiaSigno que explora cada columna buscando cambios de signo en el coeficiente de orden j, tras sucesivas iteraciones. Si no detecta ningún cambio de signo devuelve false, y si encuentra un cambio de signo, quiere decir, que ha encontrado una raíz compleja y su correspondiente conjugada, añadiéndose una unidad al contador numComplejas. Posteriormente, calcula el módulo de dicha raíz, y por último, devuelve true.
private boolean cambiaSigno(int j){
for(int k=2; k<=m; k++){
if(a[k][j]>0) continue;
//.....
return true;
}
return false;
}
El módulo de las raíces complejas se determina mediante la misma fórmula que las raíces dobles., calculando la raíz 2*2m de la razón de los coeficientes que inmediatamente preceden y siguen al coeficiente excepcional.
Para calcular una raíz compleja hemos de determinar su parte real, ya que la parte imaginaria se obtiene a partir de su módulo y de su parte real.
Denotemos las raíces complejas como u+vi y u-vi, si conocemos la parte
real u, la parte imaginaria v se determina mediante la fórmula
![]() , donde r es el módulo obtenido a partir de la
fórmula (5). Queda, por tanto, determinar la parte real u, mediante la fórmula
que daremos sin justificar.
, donde r es el módulo obtenido a partir de la
fórmula (5). Queda, por tanto, determinar la parte real u, mediante la fórmula
que daremos sin justificar.
![]()
En el código de la función denominada unaRaizCompleja, primero se calcula la suma de todas las raíces reales. Luego, se determina u, y a partir de u se calcula v. La raíz compleja y su correspondiente conjugada se guardan el array raicesComplejas.
private void unaRaizCompleja(){
double suma=0.0;
for(int i=0; i<numReales; i++){
suma+=raicesReales[i];
}
double u, v;
u=-(a[0][1]+suma)/2;
v=Math.sqrt(moduloComplejas[0]*moduloComplejas[0]-u*u);
raicesComplejas[0]=new Complejo(u, v);
raicesComplejas[1]=new Complejo(u, -v);
}
|
En esta porción de código, hemos empleado un nuevo tipo de dato, denominado Complejo. Se trata de una clase cuyos miembros dato son la parte real y la parte imaginaria del número complejo, y como funciones miembro tiene los constructores, las funciones que suman, restan, multiplican o dividen dos numeros complejos.
Supongamos ahora el polinomio ![]() que tiene una
raíz real 2, y dos raíces complejas y sus correspondientes conjugadas, 2+3i, 2-3i, -1+i,
-1-i. Examinando la tabla vemos que los coeficientes segundo a1
y quinto a4 cambian de signo, y además, se
comportan de modo similar al de las raíces
dobles, signo inequívoco de una raíz compleja. Por tanto, el polinomio tendrá dos
raíces complejas y sus respectivas conjugadas, en total cuatro raíces que es el máximo
número que permite este procedimiento.
que tiene una
raíz real 2, y dos raíces complejas y sus correspondientes conjugadas, 2+3i, 2-3i, -1+i,
-1-i. Examinando la tabla vemos que los coeficientes segundo a1
y quinto a4 cambian de signo, y además, se
comportan de modo similar al de las raíces
dobles, signo inequívoco de una raíz compleja. Por tanto, el polinomio tendrá dos
raíces complejas y sus respectivas conjugadas, en total cuatro raíces que es el máximo
número que permite este procedimiento.
| m (2m) | a0 | a1 | a2 | a3 | a4 | a5 |
| 0 (1) | 1.0 | -4.0 | 11.0 | 4.0 | -10-0 | -52.0 |
| 1 (2) | 1.0 | -6.0 | 133.0 | 652.0 | 516.0 | 2704.0 |
| 2 (4) | 1.0 | -230.0 | 2.6545 104 | 2.554 105 | -3.2598 106 | 7.3116 106 |
| 3 (8) | 1.0 | -190.0 | 8.156 108 | 2.3493 1011 | 6.8913 1012 | 5.346 1013 |
| 4 (16) | 1.0 | -1.6312 109 | 6.6531 1017 | 4.3949 1022 | 2.2371 1025 | 2.8579 1027 |
| 5 (32) | 1.0 | 1.3301 1018 | 4.4278 1035 | 1.9018 1045 | 2.4926 1050 | 8.1678 1054 |
| 6 (64) | 1.0 | 8.8357 1035 | 1.9605 1071 | 3.6165 1090 | 3.1066 10100 | 6.6714 10109 |
| 7 (128) | 1.0 | 3.886 1061 | 3.8437 10142 | 1.3079 10181 | 4.8255 10200 | 4.4507 10219 |
| 8 (256) | 1.0 | 7.4134 10142 | 1.4774 10275 | 1.7107 10362 | 1.1643 10401 | 1.9809 10439 |
| 9 (512) | 1.0 | 2.5411 10285 | 2.1827 10570 | 2.9265 10724 | 6.7774 10801 | 3.9238 10878 |
Denotaremos las dos raíces complejas y sus respectivas conjugadas como
![]() y
y ![]() . Conocidos u1
y u2 se calcula v1 y v2 mediante las
fórmulas
. Conocidos u1
y u2 se calcula v1 y v2 mediante las
fórmulas
![]()
Para determinar u1 y u2 se emplean las siguientes fórmulas
![]()
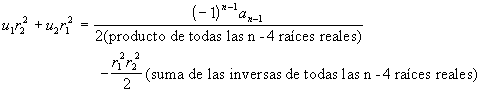
Se trata de un sistema de dos ecuaciones con dos incógnitas de las que se despeja u1 y u2
En la función denominada dosRaicesComplejas, la primera tarea será la de calcular la suma de todas las raíces reales, el producto, y la suma de las inversas de dichas raíces.
Después calcularemos los segundos miembros de cada una de las dos ecuaciones y los guardaremos en las variables locales y y z
La solución del sistema de dos ecuaciones con dos incógnitas es
![]()
lo que nos permite calcular u1 y u2 y posteriormente, v1 y v2
Finalmente, guardamos los valores obtenidos en el array raicesComplejas
private void dosRaicesComplejas(){
double suma=0.0;
double producto=1.0;
double inversa=0.0;
for(int i=0; i<numReales; i++){
suma+=raicesReales[i];
producto*=raicesReales[i];
inversa+=1/raicesReales[i];
}
double r1=moduloComplejas[0];
double r2=moduloComplejas[1];
double y=-(a[0][1]+suma)/2;
int signo=((n-1)%2==0)? +1: -1;
double z=signo*a[0][n-1]/(2*producto)-r1*r1*r2*r2*inversa/2;
double u1=(y*r1*r1-z)/(r1*r1-r2*r2);
double u2=(-y*r2*r2+z)/(r1*r1-r2*r2);
double v1=Math.sqrt(r1*r1-u1*u1);
double v2=Math.sqrt(r2*r2-u2*u2);
raicesComplejas[0]=new Complejo(u1, v1);
raicesComplejas[1]=new Complejo(u1, -v1);
raicesComplejas[2]=new Complejo(u2, v2);
raicesComplejas[3]=new Complejo(u2, -v2);
}
|