Medidas de longitud
La cinta métrica


Expresamos correctamente la medida, el error y la unidad
La longitud de la pieza es 13.3 ±0.1 cm
El micrómetro

Lee directamente el número de milímetros sobre el cuerpo graduado que deja al descubierto la caberza giratoria y las centésimas en el nonio giratorio. Si el número de centésimas es superior a 50, habrá aparecido la raya correspondiente a los medios milímetos en el cuerpo graduado (tal como se aprecia en la segunda figura)

El espesor de la pieza es 4.16 ±0.01 mm

El espesor de la pieza es 8.64 ±0.01 mm
El calibre

El calibre es un aparato empleado para la medida de espesores y diámetros interiores y exteriores. Consta de una regla provista de un nonius.
El nonius es un aparato destinado a la medida precisa de longitudes o de ángulos. El empleado para la medida de longitudes consta de una regla dividida en partes iguales, sobre la que desliza una reglilla graduada (nonius) de tal forma que n-1 divisiones de la regla se dividen en n partes iguales del nonius.
Si D es la longitud de una de las divisiones de la regla, la longitud de una división de nonius es d=D(n-1)/n
Se llama precisión p a la diferencia entre las longitudes de una división de la regla y otra del nonius. Su valor es:
Así, si cada división de la regla tiene por longitud un milímetro, y se han dividido nueve divisiones de ella en diez del nonius, la precisión es de 1/10 de mm (nonius decimal).
Medidas con el calibre

La longitud de la pieza es 21.9 ±0.1 mm
Simulación del calibre
El programa interactivo nos muestra una parte de la regla en color amarillo y el nonius en color azul claro
Al pulsar el botón Nuevo, se genera una medida. Se introduce la medida en el control titulado Medida y se pulsa el botón Mide. Un mensaje nos indica si se ha introducido la medida correcta, si faltan decimales, etc.
Si no se acierta, se pulsa el botón titulado Ayuda, una flecha roja en la regla marca la parte entera y otra flecha en el nonius marca la parte decimal de la medida.
Se introducirá como separador entre la parte entera y la parte decimal el punto (.) en vez de la coma (,).
Práctica de laboratorio

Volumen de una esfera
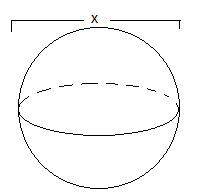
El volumen de una esfera de diámetro x es
El volunen V es una función de una sola variable x. El error es
Hemos medido el diámetro de una esfera con un calibre x=17.2±0.1 mm.
>> format long g >> x=17.2; >> V=pi*x^3/6 V = 2664.30514249561 >> dV=pi*x^2*0.1/2 dV = 46.4704385319002
| V±ΔV | 2660±50 mm3 |
|---|
Medida del volumen de un prisma de lados a, b, c
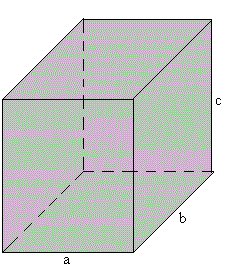
| Lado | Medida, error y unidad |
|---|---|
| a±Δa | 63.8±0.1 mm |
| b±Δb | 13.0±0.1 mm |
| c±Δc | 12.9±0.1 mm |
>> format long g >> a=63.8; >> b=13.0; >> c=12.9; >> V=a*b*c V = 10699.26 >> dV=V*sqrt((0.1/a)^2+(0.1/b)^2+(0.1/c)^2) dV = 118.04192350178
Volumen, error y unidad
| V±ΔV | 10700±100 mm3 |
|---|
Medida del volumen de un cilindro de diámetro d y altura h
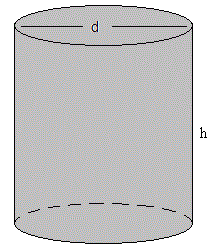
| Lado | Medida, error y unidad |
|---|---|
| d±Δd | 23.9±0.1 mm |
| h±Δh | 63.6±0.1 mm |
>> format long g >> d=23.9; >> h=63.6; >> V=pi*d^2*h/4 V = 28532.6953205467 >> dV=V*sqrt((2*0.1/d)^2+(0.1/h)^2) dV = 242.945466777225
Volumen, error y unidad
| V±ΔV | 28500±200 mm3 |
|---|
Densidad del cilindro
Con una balanza pesamos el cilindro cuyo volumen hemos medido en el ejemplo anterior
| m±Δm | 208.6±0.1 g |
|---|---|
| V±ΔV | 28.5±0.2 cm3 |
La densidad es el cociente entre la masa y el volumen, ρ=m/V
El error cometido en la medida de la densidad es
>> format long g >> m=208.6; >> V=28.5; >> rho=m/V rho = 7.31929824561403 >> d_rho=rho*sqrt((0.1/m)^2+(0.2/V)^2) d_rho = 0.0514832035628915
| ρ±Δρ | 7.32±0.05 g/cm3 |
|---|

