Reglas para expresar una medida y su error

Cuando un físico mide algo debe tener gran cuidado para no producir una perturbación en el sistema que está bajo observación. Por ejemplo, cuando medimos la temperatura de un cuerpo, lo ponemos en contacto con un termómetro. Pero cuando los ponemos juntos, algo de energía o "calor" se intercambia entre el cuerpo y el termómetro, dando como resultado un pequeño cambio en la temperatura del cuerpo que deseamos medir. Así, el instrumento de medida afecta de algún modo a la cantidad que deseábamos medir

Además, todas las medidas está afectadas en algún grado por un error experimental debido a las imperfecciones inevitables del instrumento de medida, o las limitaciones impuestas por nuestros sentidos que deben de registrar la información.

Por ejemplo, al medir una cierta distancia hemos obtenido

297±2 mm.

De este modo, entendemos que la medida de dicha magnitud está en alguna parte entre 295 mm y 299 mm. En realidad, la expresión anterior no significa que se está seguro de que el valor verdadero esté entre los límites indicados, sino que hay cierta probabilidad de que esté ahí.

Una medida de una velocidad expresada de la forma

6051.78±30 m/s

es completamente ridícula, ya que la cifra de las decenas puede ser tan pequeña como 2 o tan grande como 8. Las cifras que vienen a continuación 1, 7 y 8 carecen de significado y deben de ser redondeadas. La expresión correcta es

6050±30 m/s

Una medida de 92.81 con un error de 0.3, se expresa

92.8±0.3

Con un error de 3, se expresa

93±3

Con un error de 30 se expresa

90±30

Los errores se deben dar solamente con una única cifra significativa. Únicamente, en casos excepcionales, se pueden dar una cifra y media (la segunda cifra 5 ó 0).

Expresiones incorrectas: el error se debe dar con una sola cifra significativa

24467±2928 m

23.463±0.165 cm

345.20±3.10 mm

Expresiones incorrectas: la medida y el error tienen el mismo orden de magnitud.

24467±3000 cm

43±0.06 m

345.2±3 m

Expresiones correctas

24000±3000 m

23.5±0.2 cm

345±3 m

43.00±0.06 m

Medidas directas

Un experimentador que haga la misma medida varias veces no obtendrá, en general, el mismo resultado, no sólo por causas imponderables como variaciones imprevistas de las condiciones de medida: temperatura, presión, humedad, etc., sino también, por las variaciones en las condiciones de observación del experimentador.

Si al tratar de determinar una magnitud por medida directa realizamos varias medidas con el fin de corregir los errores aleatorios, los resultados obtenidos son x₁, x₂, ... x_n se adopta como mejor estimación del valor verdadero, el valor medio <x>, que viene dado por

${\displaystyle <x>=\frac{x_1+x_2+\mathrm{...}{x}_n}{n}=\frac{\sum _1^n{x}_i}{n}}$

El valor medio, se aproximará tanto más al valor verdadero de la magnitud cuanto mayor sea el número de medidas, ya que los errores aleatorios de cada medida se va compensando unos con otros.

Sin embargo, en la práctica, no debe pasarse de un cierto número de medidas. En general, es suficiente con 10, e incluso podría bastar 4 ó 5.

Cuando la sensibilidad del método o de los aparatos utilizados es pequeña comparada con la magnitud de los errores aleatorios, puede ocurrir que la repetición de la medida nos lleve siempre al mismo resultado; en este caso, está claro que el valor medio coincidirá con el valor medido en una sola medida, y no se obtiene nada nuevo en la repetición de la medida y del cálculo del valor medio, por lo que solamente será necesario en este caso hacer una sola medida.

Los errores se producen por causas aleatorias, se toma como la mejor estimación del error, el llamado error cuadrático

${\displaystyle \Delta x=\sqrt{\frac{\sum _1^n{(x_i-<x>)}^2}{n(n-1)}}}$

El resultado del experimento se expresa como

<x>±Δx y la unidad de medida

Es evidente, por ejemplo, tomando el caso más extremo, que si el resultado de las n medidas ha sido el mismo, el error cuadrático, de acuerdo con la formula será cero, pero eso no quiere decir que el error de la medida sea nulo. Sino, que el error instrumental es tan grande, que no permite observar diferencias entre las diferentes medidas y por tanto, el error instrumental, aquél que viene definido por la resolución del aparato de medida, será el error de la medida.

Ejemplos:

1. Si al hacer una medida de la intensidad con un amperímetro cuya división o cifra significativa más pequeña es 0.01 A, la lectura es 0.64 A, y esta lectura es constante (no se observan variaciones al medir en diferentes instantes), tomaremos 0.64 como el valor de la medida y 0.01 A como su error. La medida se expresará así

0.64±0.01 A

2. Supongamos que hemos medido un determinado tiempo, t, cuatro veces, y disponemos de un cronómetro que permite conocer hasta las décimas de segundo. Los resultados han sido: 6.3, 6.2, 6.4 y 6.2 s. De acuerdo a lo dicho anteriormente, tomaremos como valor medido el valor medio:

${\displaystyle <t>=\frac{6.3+6.2+6.4+6.2}{4}=6.275s}$

El error cuadrático será

${\displaystyle \Delta t=\sqrt{\frac{{(6.3-6.275)}^2+{(6.2-6.275)}^2+{(6.4-6.275)}^2+{(6.2-6.275)}^2}{4\cdot 3}}}$

>> x=[6.3 6.2 6.4 6.2];
>> media=mean(x)
media =    6.2750
>> error=std(x)/sqrt(length(x))
error =    0.0479

Este error se expresa con una sola cifra significativa, Δt=0.05 s. Pero el error cuadrático es menor que el error instrumental, que es 0.1 s, por lo que debemos tomar este último como el error de la medida y redondear en consecuencia el valor medio, por lo que el resultado final de la medida es

t=6.3±0.1 s

3. Consideremos un ejemplo similar al anterior, pero en que los valores obtenidos para el tiempo están más dispersos: 5.5, 5.7, 6.2 y 6.5 s. Se encuentra que el valor medio es 5.975, y el error cuadrático 0.2286737.

>> x=[5.5 5.7 6.2 6.5];
>> media=mean(x)
media =    5.9750
>> error=std(x)/sqrt(length(x))
error =    0.2287

El error cuadrático es en esta caso mayor que el error instrumental, por lo que debemos tomarlo como el error de la medida. Lo debemos redondear a 0.2 (una sola cifra significativa). Expresamos la medida finalmente como

t=6.0±0.2 s

Medidas indirectas

En muchos casos, el valor experimental de una magnitud se obtiene, de acuerdo a una determinada expresión matemática, a partir de la medida de otras magnitudes de las que depende.

Funciones de una sola variable

1. Se desea calcular el índice de refracción n de un vidrio midiendo el ángulo crítico θ, mediante la fórmula n=1/sinθ. Si medimos el ángulo θ es fácil calcular el índice de refracción n. Pero si conocemos el error de la medida del ángulo, necesitamos conocer el error del índice de refracción.

Sea una función y=y(x). Como se aprecia en la figura, si el error Δx es pequeño. El error Δy se calcula del siguiente modo



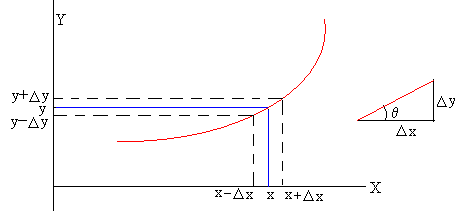
Δy=tanθ·Δx

Pero tanθ es la pendiente de la recta tangente a al curva en el punto de abscisa x



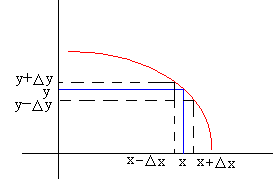
Como la pendiente puede ser positiva, si la función es creciente o negativa si la función es decreciente, en general tendremos que

${\displaystyle \Delta y=\left|f\text{'}(<x>)\right|\Delta x}$

Sea y=cos x

Sea x=20±3 º,

y=cos20=0.9397

El error Δx=3π/180=0.0524 rad

Δy=|sin20|·0.0524=0.018

y=0.94±0.02

2. Supongamos que queremos medir el periodo P de un oscilador, es decir, el tiempo que tarda en efectuar una oscilación completa, disponemos de un cronómetro que aprecia las décimas de segundo, 0.1 s. Medimos el tiempo que tarda en hacer 10 oscilaciones, por ejemplo 4.6 s, dividiendo este tiempo entre 10 resulta P=0.46 s, que es el periodo "medio".

${\displaystyle P=\frac{t}{10}\Delta P=\frac{\Delta t}{10}}$

Obtenemos para el error ΔP=0.01 s. Expresamos la medida como

P=0.46±0.01 s

Es evidente, que podemos aumentar indefinidamente la resolución instrumental para medir P, aumentando el número de periodos que incluimos en la medida directa de t. El límite está en nuestra paciencia y la creciente probabilidad de cometer errores cuando contamos el número de oscilaciones. Por otra parte, el oscilador no se mantiene con la misma amplitud indefinidamente, sino que se para al cabo de un cierto tiempo.

Función de varias variables

La magnitud y viene determinada por la medida de varias magnitudes p, q, r, etc., con la que está ligada por la función

y=f(p, q, r ...).

El error de la magnitud y viene dado por la siguiente expresión.

${\displaystyle \Delta y=\sqrt{{\left(\langle \frac{\partial f}{\partial p}\rangle \Delta p\right)}^2+{\left(\langle \frac{\partial f}{\partial q}\rangle \Delta q\right)}^2+{\left(\langle \frac{\partial f}{\partial r}\rangle \Delta r\right)}^2+\mathrm{...}}}$

Casos más frecuentes

${\displaystyle \begin{array}{l}z=x+y\Delta z=\sqrt{\Delta x^2+\Delta y^2}\\ z=x-y\Delta z=\sqrt{\Delta x^2+\Delta y^2}\\ z=x\cdot y\frac{\Delta z}{z}=\sqrt{{\left(\frac{\Delta x}{x}\right)}^2+{\left(\frac{\Delta y}{y}\right)}^2}\\ z=\frac{x}{y}\frac{\Delta z}{z}=\sqrt{{\left(\frac{\Delta x}{x}\right)}^2+{\left(\frac{\Delta y}{y}\right)}^2}\end{array}}$

Ejemplo 1: La medida de los lados de un rectángulo son 1.53±0.06 cm, y 10.2±0.1 cm, respectivamente. Hallar el área del rectángulo y el error de la medida indirecta.

El área es z=1.53×10.2=15.606 cm²

>> x=1.53; dx=0.06;
>> y=10.2; dy=0.1;
>> z=x*y
z =   15.6060
>> dz=z*sqrt((dx/x)^2+(dy/y)^2)
dz =    0.6308

El error en el área Δz/z se obtiene aplicando la fórmula del producto de dos magnitudes.

${\displaystyle \begin{array}{l}\frac{\Delta z}{z}=\sqrt{{\left(\frac{0.06}{1.53}\right)}^2+{\left(\frac{0.1}{10.2}\right)}^2}=0.0404422504\\ \Delta z=\left(1.53\cdot 10.2\right)\cdot 0.0404422504=0.63083\end{array}}$

El error con una sola cifra significativa es 0.6. La medida del área junto con el error y la unidad se escribirá correctamente

z=15.6±0.6 cm²

Ejemplo 2: Queremos calcular la aceleración de la gravedad g, midiendo el periodo P de las oscilaciones de un péndulo de longitud l

${\displaystyle P=2\pi \sqrt{\frac{l}{g}}g=4{\pi }^2\frac{l}{P^2}}$

La expresión del error Δg de la variable dependiente g es

${\displaystyle \begin{array}{l}\Delta g=\sqrt{{\left(4{\pi }^2\frac{1}{P^2}\Delta l\right)}^2+{\left(4{\pi }^2\frac{-2l}{P^3}\Delta P\right)}^2}=4{\pi }^2\frac{l}{P^2}\sqrt{{\left(\frac{\Delta l}{l}\right)}^2+{\left(\frac{2\Delta P}{P}\right)}^2}\\ \frac{\Delta g}{g}=\sqrt{{\left(\frac{\Delta l}{l}\right)}^2+{\left(\frac{2\Delta P}{P}\right)}^2}\end{array}}$

Supongamos que medimos el periodo P y la longitud l del péndulo

P=1.95±0.01 s
l=94±1 cm

Calculamos la aceleración de la gravedad y el error

g=9.759293 m/s²
Δg=0.144

Expresamos correctamente la medida y el error de g

g=9.8±0.1 m/s²

Utilizando el Symbolic Math Toolbox de MATLAB

>> syms l P dl dP;
>> g=4*sym('pi')^2*l/P^2;
>> gg=subs(g,{P,l},{1.95,0.94})
gg =(1504*pi^2)/1521
>> double(gg)
ans =    9.7593

>> dg=sqrt((diff(g,l)*dl)^2+(diff(g,P)*dP)^2);
>> simplify(dg)
ans =4*pi^2*((P^2*dl^2 + 4*dP^2*l^2)/P^6)^(1/2)
>> dgg=subs(dg,{P,l,dP,dl},{1.95,0.94,0.01,0.01}) 
dgg =4*((1173904*pi^4)/87968594025)^(1/2)
>> double(dgg)
ans =    0.1442	 

Ejemplo 3: Queremos calcular el índice de refracción de un vidrio, midiendo el ángulo que hace el rayo incidente y el rayo refractado con la normal. Aplicamos la ley de Snell de la refracción

${\displaystyle n=\frac{\sin i}{\sin r}}$

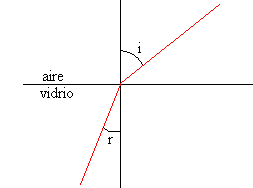
Cálculo del error en la medida del índice de refracción n.

${\displaystyle \frac{\Delta n}{n}=\sqrt{{\left(\frac{1}{\tan i}\Delta i\right)}^2+{\left(\frac{1}{\tan r}\Delta r\right)}^2}}$

Sea i=20±1º y r=13±1º.
1º=π/180 rad

Se calcula el índice de refracción n y el error Δn

>> syms i r di dr;
>> n=sin(i)/sin(r);
>> nn=subs(n,{i,r},{20*pi/180,13*pi/180});
>> double(nn)
ans =    1.5204

>> dn=sqrt((diff(n,i)*di)^2+(diff(n,r)*dr)^2);
>> simplify(dn)
ans =((di^2*cos(i)^2*sin(r)^2 + dr^2*cos(r)^2*sin(i)^2)/sin(r)^4)^(1/2)
>> dnn=subs(dn,{i,r,di,dr},{20*pi/180,13*pi/180,pi/180,pi/180});
>> double (dnn)
ans =    0.1361 

n=1.52
Δn=0.136

Expresamos correctamente la medida y el error de n

n=1.5±0.1

Referencias

Taylor J. R. An Introduction to Error Analysis. The Study of Uncertainties in Physical Measurements. University Science Books (1982)