Para pesar un determinado objeto, se desplazan masas calibradas a lo largo de tres rieles y se fijan en posiciones etiquetadas. Las divisiones de las balanzas del laboratorio de Física de la Escuela de Ingeniería de Eibar son las que se ven en la imagen:

• de 0 g hasta 500 g en divisiones de 100 g
• de 0 g hasta 100 g en divisiones de 10 g
• de 0 g hasta 10 g en divisiones de 0.1 g

Medida de la masa de un cuerpo

En el programa interactivo (más abajo) la balanza solamente aprecia gramos, el error que se comete en una medida es ± 1 g. Por ejemplo, si se ha pesado un cuerpo y de la lectura de los indicadores de la balanza se ha obtenido la cifra de 234. La medida del peso de dicho cuerpo se expresa como

234 ± 1 g

Medida del volumen de un cuerpo irregular

Para medir la densidad de un cuerpo es necesario conocer su masa y su volumen.

Si el cuerpo es irregular, determinamos su volumen de forma indirecta aplicando el principio de Arquímedes.

"Todo cuerpo sumergido en un fluido experimenta un empuje igual al peso del volumen de líquido desalojado"

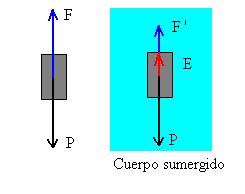
A la izquierda tenemos que la tensión F de la cuerda es igual al peso del cuerpo. Sumergiendo completamente el cuerpo en agua, la tensión de la cuerda que sujeta al cuerpo F’=P-E disminuye debido al empuje E del agua.

Por la tercera ley de Newton, el cuerpo emuja al agua con una fuerza igual y de sentido contrario E. Lo que nos marca la balanza es la suma de dos fuerzas: el peso del recipiente y del agua que contiene, y el empuje E tal como se muestra en las dos fotografías de la balanza: antes de sumergir el cuerpo y después.

Si el fluido es agua, cuya densidad es la unidad, el peso en gramos coincide numéricamente con el volumen medido en centímetros cúbicos.

El empuje es igual a la diferencia entre lo que marca la balanza antes y después de sumergir el cuerpo en agua e igual numéricamente al volumen del cuerpo en centímetros cúbicos.

V=F-F’

Error en la medida del volumen.

De las fórmulas de los errores en las medidas indirectas se obtiene que el error de una diferencia

${\displaystyle \Delta V=\sqrt{{\left(\Delta F\right)}^2+{\left(\Delta F\text{'}\right)}^2}}$

Como ΔF=ΔF’=1 , se obtiene que ΔV=1.41. Expresando el error con una sola cifra significativa, ΔV=1

Cálculo de la densidad del cuerpo sólido

Se define la densidad como el cociente entre la masa y el volumen de un cuerpo.

${\displaystyle \rho =\frac{m}{V}}$

De las fórmulas de los errores en las medidas indirectas, se obtiene que el error de un cociente

${\displaystyle \frac{\Delta \rho }{\rho }=\sqrt{{\left(\frac{\Delta m}{m}\right)}^2+{\left(\frac{\Delta V}{V}\right)}^2}}$

donde Δm=ΔV=1.

Una vez obtenidas las medidas de m y de V, se calcula el error en la medida de la densidad Δρ.

Actividades

Para medir la masa de un cuerpo se pulsa sobre el botón titulado Masa. Se desplazan los cursores a lo largo de las guías actuando con el ratón. Se pulsa el botón izquierdo del ratón cuando el puntero está sobre un cursor, se arrastra el ratón, el cursor se desplaza automáticamente a la siguiente posición sobre la guía. Se deja de pulsar el botón izquierdo del ratón, cuando el cursor está situada en la marca deseada.

La balanza está equilibrada cuando el brazo está en posición horizontal y la flecha azul apunta a la marca roja situada a su derecha. El mismo procedimiento se emplea para medir el volumen pulsando el botón titulado Volumen.

• Se selecciona una sustancia en el control selección titulado Material.
• Se pulsa el botón titulado Masa. Se mide la masa del cuerpo
• Se pulsa el botón titulado Volumen. Se mide el volumen del cuerpo, hallando la diferencia de las medidas de los pesos del mismo cuerpo antes y después de sumergirlo en agua.
• Se calcula la densidad y el error en la medida de la densidad, expresando correctamente la medida, el error y la unidad de medida.

Ejemplo:

Se elige Cobre en el control titulado Materiales

1. Pulsando el botón titulado Masa, se genera una pieza hecha de cobre de masa y volumen desconocido.

Con la balanza medimos su masa: m=410 ±1 g.

2. Pulsamos el botón titulado Volumen y el cuerpo se sumerge en agua.

Efectuamos una nueva medida con la balanza m’=364 g. El volumen es numéricamente igual al empuje, la diferencia entre ambas medidas. V=410-364=46. La medida del volumen es 46 ± 1 cm³

3. Cálculo de la densidad

${\displaystyle \rho =\frac{410}{46}=8.913\Delta \rho =8.913\sqrt{{\left(\frac{1}{410}\right)}^2+{\left(\frac{1}{46}\right)}^2}=0.195}$

4. La densidad se expresa

ρ=8.9± 0.2 g/cm³