Movimiento de la cinta de una casete

Una casete es una caja de plástico que dispone de dos pequeñas ruedas en las que se enrolla y desenrolla respectivamente una cinta magnética. Dispone de un cabezal que graba o reproduce el sonido en la cinta, tal como se muestra en la figura.

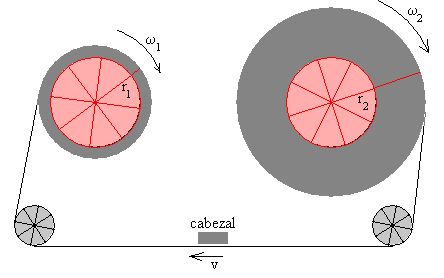
La casete

El radio inicial de las ruedas sin cinta es r₀=1.11 cm, y la velocidad de la cinta cuando pasa por el cabezal es constante e igual a v=4.76 cm/s. La cinta tarda un tiempo T en reproducirse completamente. Este tiempo depende de la longitud total de la cinta l=v·T. El espesor de la cinta h es muy pequeño, y su valor lo determinaremos más adelante.

En el instante inicial t=0.

El radio de la rueda izquierda es r₀=1.11 cm
El radio de la rueda derecha es R₀=2.46 cm, para una cinta de duración T=46.4 minutos

La cinta se desenrolla de la rueda derecha y se enrolla en la izquierda. En un instante determinado t, la relación entre la velocidad lineal constante v de la cinta y las velocidades angulares de rotación de las ruedas serán

El radio de la rueda izquierda será r₁ y su velocidad angular ω₁=v/r₁
El radio de la rueda derecha será r₂ y su velocidad angular ω₂=v/r₂

Aunque la velocidad v de la cinta es constante, las velocidades angulares ω₁ y ω₂ de las ruedas no lo son ya que sus radios r₁ y r₂ cambian con el tiempo

En cada vuelta 2π, la rueda izquierda incrementa su radio en h, el espesor de la cinta. Cuando la rueda izquierda gira un ángulo dθ₁, su radio se habrá incrementado en dr₁.

$d r_{1} = \frac{h}{2 π} d θ_{1} = \frac{h}{2 π} ω_{1} d t = \frac{h}{2 π} \frac{v}{r_{1}} d t$

La rueda derecha habrá girado un ángulo dθ₂, su radio habrá disminuido en dr₂

$d r_{2} = - \frac{h}{2 π} d θ_{2} = - \frac{h}{2 π} ω_{2} d t = - \frac{h}{2 π} \frac{v}{r_{2}} d t$

Integramos estas dos ecuaciones entre el instante t=0, y en el instante t, teniendo en cuenta que en el instante t=0,

el radio de la rueda izquierda es r₁=r₀
el radio de la rueda derecha es r₂=R₀

$r_{1}^{2} = r_{0}^{2} + \frac{h v}{π} t r_{2}^{2} = R_{0}^{2} - \frac{h v}{π} t$

En el instante t=T la cinta se ha reproducido completamente.

el radio de la rueda izquierda es r₁=R₀
el radio de la rueda derecha es r₂=r₀

$R_{0}^{2} = r_{0}^{2} + \frac{h v}{π} T r_{0}^{2} = R_{0}^{2} - \frac{h v}{π} T$

Si medimos los radios r₀ y R₀, el tiempo T, y la velocidad v podemos despejar el espesor h de la cinta de la primera o de la segunda ecuación. Si la duración de la cinta es de T=46.4 minutos.

$h = \frac{π (R_{0}^{2} - r_{0}^{2})}{v T} = \frac{π ({2.46}^{2} - {1.11}^{2})}{4.76 \cdot 46.4 \cdot 60} = 1.14 \cdot 10^{- 3} cm$

Los ángulos girados por las dos ruedas se calculan integrando ω₁, y ω₂, respecto del tiempo t.

$\begin{array}{l} \int_{0}^{t} ω_{1} d t = \int_{0}^{t} \frac{v}{r_{1}} d t = \frac{2 π}{h} (\sqrt{r_{0}^{2} + \frac{h v}{π}} t - r_{0}) = \frac{2 π}{h} (r_{1} - r_{0}) \\ θ_{2} = \int_{0}^{t} ω_{2} d t = \int_{0}^{t} \frac{v}{r_{2}} d t = \frac{2 π}{h} (R_{0} - \sqrt{R_{0}^{2} - \frac{h v}{π}} t) = \frac{2 π}{h} (R_{0} - r_{2}) \end{array}$

En el instante t=T, r₁=R₀ y r₂=r₀, el ángulo total girado por ambas ruedas es el mismo,

$θ = \frac{2 π}{h} (R_{0} - r_{0})$

Actividades

Introducimos

La duración T de la cinta en minutos, actuando sobre la barra de desplazamiento, titulada Duración cinta, o introduciendo un número en el control de edición.

Se pulsa el botón titulado Empieza

El programa interactivo utiliza el dato del espesor de la cinta h=1.14·10^-3 cm, la velocidad lineal constante v=4.76 cm/s de la cinta y el radio r₀=1.11 cm inicial de la rueda para calcular el radio R₀ la rueda derecha con la cinta completamente enrollada. Estos datos se han tomado del artículo citado en las referencias

Observaremos el movimiento de las ruedas, la relación entre la velocidad angular de rotación y su radio, a medida que transcurre el tiempo. En la parte superior del applet, se muestran en cada instante, los valores de r₁, ω₁, r₂ y ω₂. Comprobar que

r₁·ω₁=r₂·ω₂=v=4.76 m/s