Un dispositivo mecánico simple

En la página anterior, se ha descrito el péndulo cónico, que se caracteriza por una velocidad angular critica ω_c a partir de la cual el péndulo se desvía un cierto ángulo de de su posición vertical. Por debajo de esta velocidad angular crítica, el péndulo permanece en la posición vertical θ =0.

Un dispositivo similar es un aro de radio R que puede girar alrededor de su diámetro vertical con velocidad angular ω. Un punto material de masa m se mueve a lo largo de la circunferencia sin rozamiento.

Ambos sistemas, se pueden describir por una energía potencial efectiva debida al peso de la partícula y a la fuerza centrífuga.

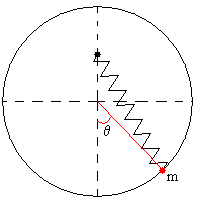El sistema que vamos a estudiar ahora no hay fuerzas de inercia ya que consiste en una partícula de masa m que se mueve a lo largo de una circunferencia de radio R sin rozamiento. La partícula está unida al extremo de un muelle de constante k tal como se muestra en la figura

La energía potencial

La energía potencial de la partícula se compone de dos términos:

La energía potencial gravitatoria, mg(R-R·cosθ)
La energía potencial elástica, debida a la deformación del muelle

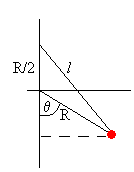
La longitud l del muelle deformado es

$l = {\sqrt{{(R \cdot \sin θ)}^{2} + (\frac{R}{2} + R \cos θ)}}^{2} = \frac{R}{2} \sqrt{5 + 4 \cos θ}$

Como la longitud del muelle sin deformar es R/2, la energía potencial debida a ambas fuerzas conservativas es

$E_{p} (θ) = m g R (1 - \cos θ) + \frac{1}{8} k R^{2} {(\sqrt{5 + 4 \cos θ} - 1)}^{2}$

Posiciones de equilibrio

La fuerza tangencial que actúa sobre la partícula es

$F (θ) = - \frac{\partial E_{p}}{\partial (R θ)} = (- m g + \frac{1}{2} k R (1 - \frac{1}{\sqrt{5 + 4 \cos θ}})) \sin θ$

Las posiciones de equilibrio se obtienen cuando F(θ)=0

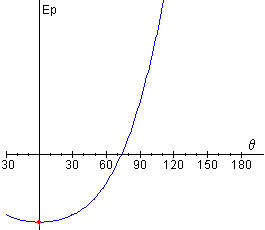
θ=0, θ=π y el ángulo θ₀ raíz de la ecuación trascendente

$\frac{1}{\sqrt{5 + 4 \cos θ}} = 1 - \frac{2 m g}{k R}$

Estabilidad

Calculamos la derivada segunda de la energía potencial

$\frac{\partial^{2} E_{p}}{\partial {(R θ)}^{2}} = (\frac{m g}{R} - \frac{1}{2} k (1 - \frac{1}{\sqrt{5 + 4 \cos θ}})) cos θ - \frac{k \sin^{2} θ}{{(5 + 4 \cos θ)}^{3 / 2}}$

Para θ=0

$\frac{\partial^{2} E_{p}}{\partial {(R θ)}^{2}} = \frac{m g}{R} - \frac{1}{3} k$

La derivada segunda es positiva (equilibrio estable) si $k < \frac{3 m g}{R}$

Para θ=π

$\frac{\partial^{2} E_{p}}{\partial {(R θ)}^{2}} = - \frac{m g}{R}$

La derivada segunda es negativa, por lo que la posición de equilibrio es inestable

Para θ= θ₀

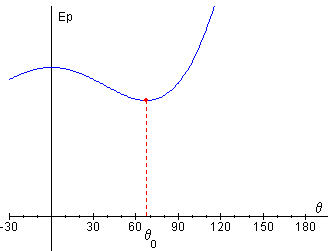
$\frac{\partial^{2} E_{p}}{\partial {(R θ)}^{2}} = k {(1 - \frac{2 m g}{k R})}^{3} \sin^{2} θ$

Esta derivada es positiva si $k > \frac{2 m g}{R}$

Ahora bien, examinemos la ecuación que nos da la raíz θ₀.

$\frac{1}{\sqrt{5 + 4 \cos θ}} = 1 - \frac{2 m g}{k R}$

El valor mínimo del miembro izquierdo es 1/3, y el valor máximo es 1.
El valor mínimo del miembro derecho se obtiene para k=3mg/R. y el valor máximo para k→∞.

Así pues, cuando la constante k del muelle elástico es inferior al valor critico k_c=3mg/R la posición de equilibrio estable es θ=0, y cuando k>k_c, la posición de equilibrio estable es θ₀, raíz de la ecuación trascendente.

Actividades

En el programa interactivo se han fijado los valores de:

La masa de la partícula m=0.1 kg
El radio de la circunferencia R=0.5 m
La aceleración de la gravedad g=10 m/s²

Con estos datos, el valor critico de la constante elástica es k_c=3mg/R=6 N/m

Se introduce

La constante k del muelle elástico, actuando en la barra de desplazamiento titulada Constante.

Se pulsa el botón titulado Calcular.

Si k<6 la posición de equilibrio es θ=0
Si k>6, el programa interactivo calcula el ángulo de equilibrio θ₀

Se muestra a la derecha del applet, la representación gráfica de la energía potencial E_p(θ). Observar los máximos y los mínimos.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Drugowich J. R., Hipólito O. Spontaneous symmetry breaking in a simple mechanical model. Am. J. Phys. 53 (7) July 1985, pp. 690-693