Una partícula desliza sobre una pista circular que gira

Consideremos un aro de radio R que puede girar alrededor de su diámetro vertical con velocidad angular ω. Un punto material de masa m se mueve a lo largo de la circunferencia sin rozamiento. Su posición está dada por el ángulo θ tal como se señala en la figura.

Las fuerzas que actúan sobre la partícula, cuando estamos situados en el Sistema de Referencia en rotación son:

El peso mg
La fuerza centrífuga F_c=mω²Rsinθ
La reacción N de la superficie circular.

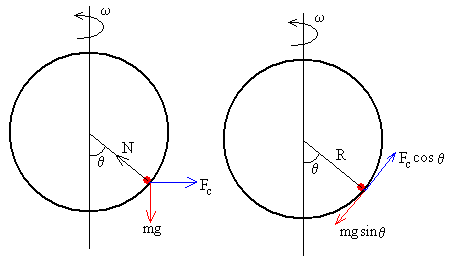
Descomponemos las fuerzas en la dirección vertical y horizontal. En la situación de equilibrio, se cumplirá que

N·cosθ =mg
N·sinθ =F_c

Que son las mismas ecuaciones que hemos obtenido en el estudio del péndulo cónico

Posiciones de equilibrio

Si descomponemos las fuerzas en la dirección tangencial y normal a la circunferencia, tendremos que en la situación de equilibrio

mg·sinθ =F_c·cosθ

La partícula está en equilibrio en la dirección normal. Si no está en equilibrio en la dirección tangencial, la fuerza neta en esta dirección es

F= -mg·sinθ +F_c·cosθ = -mg·sinθ +mω²·R·sinθ ·cosθ

Esta fuerza depende solamente de la posición θ y es conservativa. La energía potencial correspondiente a la fuerza F(θ ) es

$\int_{0}^{θ} F (θ) R \cdot d θ = E_{p} (0) - E_{P} (θ)$

Tomando como nivel cero de energía potencial E_p(0)=0 para θ=0, integramos y haciendo algunas operaciones, se obtiene

$E_{p} (θ) = m g R (1 - \cos θ) - \frac{1}{2} m ω^{2} R^{2} \sin^{2} θ$

La misma expresión que hemos obtenido en el apartado "Estabilidad de las soluciones"

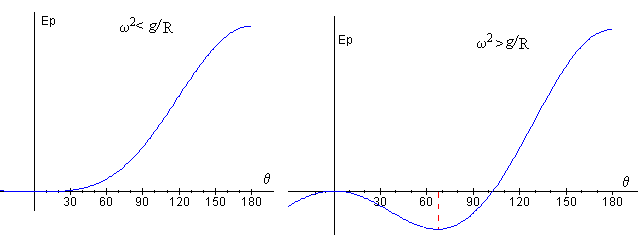
En la figura de la izquierda, vemos que para ω²<g/R la curva de la energía potencial E_p(θ) presenta un mínimo en θ_e=0 o posición de equilibrio estable.
En la figura de la derecha, vemos que para ω²>g/R la curva de la energía potencial E_p(θ) presenta un mínimo para

$θ_{e} = \arccos (\frac{g}{ω^{2} R})$ o posición de equilibrio estable y un máximo local para θ=0, posición de equilibrio inestable.

Dinámica. Sin rozamiento

Cuando situamos la partícula en la posición inicial θ₀ con velocidad inicial nula, la partícula tenderá a desplazarse hacia la posición de equilibrio. Suponiendo que no hay rozamiento, la partícula rebasará dicha posición, se detendrá y retornará a la posición de equilibrio y así, sucesivamente. La partícula oscila alrededor de la posición de equilibrio θ_e.

La ecuación del movimiento en la dirección tangencial es

$\begin{array}{l} m R \frac{d^{2} θ}{d t^{2}} = F_{c} \cos θ - m g \sin θ \\ m R \frac{d^{2} θ}{d t^{2}} = m ω^{2} R \sin θ \cos θ - m g \sin θ \\ \frac{d^{2} θ}{d t^{2}} = (ω^{2} \cos θ - \frac{g}{R}) \sin θ \end{array}$

Se resuelve esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, θ=θ₀, dθ/dt=0.

Podemos describir cualitativamente el movimiento de la partícula si trazamos su curva de energía potencial.

La partícula parte del reposo en la posición θ₀. Su energía total E es

$E = E_{p} (θ_{0}) = m g R (1 - \cos θ_{0}) - \frac{1}{2} m ω^{2} R^{2} \sin^{2} θ_{0}$

Cuando ω²<g/R

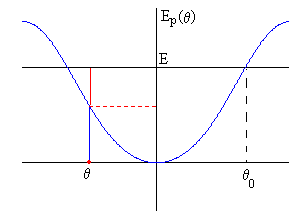
La curva de energía potencial E_p(θ) se muestra en la figura en color azul.

La partícula se desplaza desde la posición inicial θ₀ hacia la posición de equilibrio θ=0. En dicha posición, la energía potencial es mínima E_p(0)=0 y la energía cinética de la partícula es máxima, a continuación, se desplaza hasta la posición simétrica θ=-θ₀ donde su velocidad vuelve a ser cero, retornando posteriormente a la posición de equilibrio.

En la posición θ de la figura, el segmento de color azul mide la energía potencial y el segmento de color rojo, la energía cinética.

La partícula oscila alrededor de la posición de equilibrio estable θ=0 con un determinado periodo.

Cuando ω²>g/R

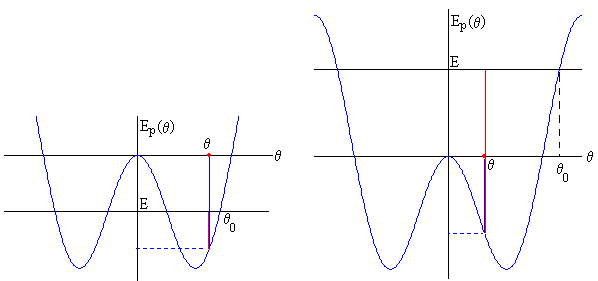
La curva de energía potencial E_p(θ) se muestra en las figuras en color azul.

La partícula se desplaza desde la posición inicial θ₀ hacia la posición de equilibrio $θ_{e} = \arccos (\frac{g}{ω^{2} R})$

En la figura de la izquierda, la energía total E<0 y la partícula oscila alrededor de la posición de equilibrio estable θ_e.

En la posición θ de la figura, el segmento de color azul mide la energía potencial y el segmento de color rojo, la energía cinética. La energía potencial es mínima en la posición de equilibrio y la energía cinética es máxima.

Los puntos de retorno, aquellos en los que la velocidad es nula y por tanto, la partícula inicia el movimiento en sentido contrario, son la posición de partida θ₀ y la raíz de la ecuación

$\begin{array}{l} E = m g R (1 - \cos θ) - \frac{1}{2} m ω^{2} R^{2} \sin^{2} θ \\ E = 2 m g R \sin^{2} \frac{θ}{2} - \frac{1}{2} m ω^{2} R^{2} \cdot 4 \sin^{2} \frac{θ}{2} \cos^{2} \frac{θ}{2} \\ E = 2 m g R \sin^{2} \frac{θ}{2} - 2 m ω^{2} R^{2} \sin^{2} \frac{θ}{2} (1 - \sin^{2} \frac{θ}{2}) \\ 2 m R ω^{2} \sin^{4} \frac{θ}{2} + 2 m R (g - ω^{2} R) \sin^{2} \frac{θ}{2} - E = 0 \end{array}$

Conocemos una de las raíces de la ecuación θ₀. La otra raíz se calcula aplicando las propiedades de las raíces de una ecuación de segundo grado

ax²+bx+c=0

Suma de raíces, x₁+x₂=-b/a
Producto de raíces, x₁·x₂=c/a

$\sin^{2} \frac{θ}{2} + \sin^{2} \frac{θ_{0}}{2} = \frac{- 2 m R (g - ω^{2} R)}{2 m R ω^{2}} = R - \frac{g}{ω^{2}}$

Ejemplo.

Velocidad angular de rotación, ω=7.0 rad/s
Radio de la pista circular, R=1.0 m
Posición angular inicial, θ₀=120º

La energía total E de la partícula vale

$E = m g R (1 - \cos 120) - \frac{1}{2} m ω^{2} R^{2} \sin^{2} 120 = - 3.675 m$

La otra solución positiva de la ecuación bicuadrada es:

$\sin^{2} \frac{θ}{2} + \sin^{2} \frac{120}{2} = 1.0 - \frac{9.8}{{7.0}^{2}} θ = 25.8 º$

Dinámica. Con rozamiento

Supongamos que el coeficiente de rozamiento entre la partícula y la superficie circular sobre la que desliza es μ. La partícula permanecerá en reposo si F_r/N<μ

La reacción N de la superficie circular es

N= mgcosθ+F_csinθ

Cuando ω²<g/R

La posición de equilibrio estable es θ_e=0

Para θ>0, la componente tangencial del peso mgsinθ es mayor que la componente tangencial de la fuerza centrífuga, F_ccosθ. La fuerza de rozamiento es la diferencia F_r= mgsinθ-F_ccosθ

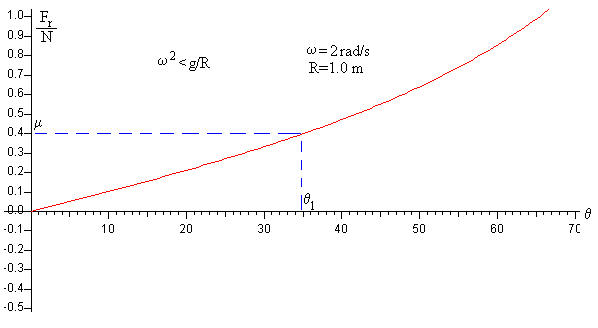
En la figura se representa F_r/N en función de θ para ω=2 rad/s, con R=1.0 m.

Dado el coeficiente de rozamiento μ, las posiciones θ para las cuales la partícula está en equilibrio serán aquellas para las que F_r/N<μ, es decir θ<θ₁.

Si la posición inicial de la partícula θ₀> θ₁ la partícula desliza hacia abajo, la velocidad angular es negativa dθ/dt<0. Las fuerzas sobre la partícula se muestran en la figura.

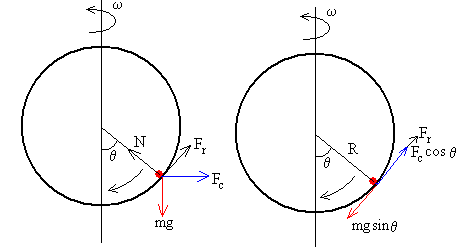
La ecuación del movimiento es

$\begin{array}{l} m R \frac{d^{2} θ}{d t^{2}} = F_{c} \cos θ - m g \sin θ + F_{r} \\ F_{r} = μ N = μ (F_{c} \sin θ + m g \cos θ) \\ \frac{d^{2} θ}{d t^{2}} = (ω^{2} \cos θ - \frac{g}{R}) \sin θ + μ (ω^{2} \sin^{2} θ + \frac{g}{R} \cos θ) \end{array}$

Se resuelve esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante t=0, θ=θ₀, dθ/dt=0.

Cuando la partícula se detiene se verifica si |F_r/N|<μ en cuyo caso la partícula permanece en reposo, en caso contrario, continua su movimiento hasta la próxima posición de parada.

Cuando ω²>g/R

La posición de equilibrio estable es $θ_{e} = \arccos (\frac{g}{ω^{2} R})$

Para θ>θ_e, la componente tangencial del peso mgsinθ es mayor que la componente tangencial de la fuerza centrífuga, F_ccosθ. La fuerza de rozamiento es la diferencia F_r= mgsinθ-F_ccosθ

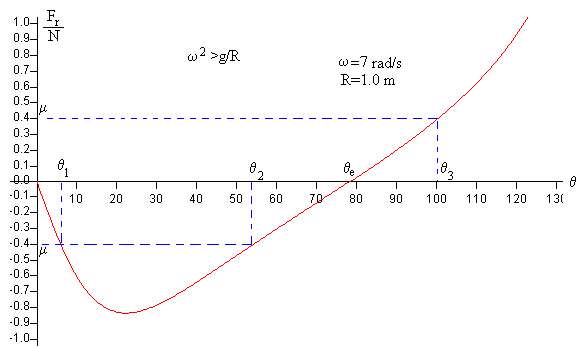
En la figura se representa F_r/N en función de θ para ω=7 rad/s, con R=1.0 m.

Dado el coeficiente de rozamiento μ, las posiciones θ para las cuales la partícula está en equilibrio serán aquellas para las que F_r/N<μ, es decir θ_e≤θ<θ₃. La fuerza de rozamiento es nula en la posición de equilibrio estable θ_e.

Si la posición inicial de la partícula θ₀> θ₃ la partícula desliza hacia abajo, la velocidad angular es negativa dθ/dt<0. Las fuerzas sobre la partícula se muestran en la figura más arriba en el caso anterior. La ecuación del movimiento es la misma

$\frac{d^{2} θ}{d t^{2}} = (ω^{2} \cos θ - \frac{g}{R}) \sin θ + μ (ω^{2} \sin^{2} θ + \frac{g}{R} \cos θ)$

Para θ<θ_e, la componente tangencial del peso mgsinθ es menor que la componente tangencial de la fuerza centrífuga, F_ccosθ. La fuerza de rozamiento es la diferencia

F_r= F_ccosθ- mgsinθ

En la figura anterior F_r/N en función de θ para θ<θ_e aparece cambiada de signo.

Dado el coeficiente de rozamiento μ, las posiciones θ para las cuales la partícula está en equilibrio serán aquellas para las que |F_r/N|<μ, es decir 0≤θ<θ₁ y θ₂<θ≤θ_e

Si la posición inicial de la partícula θ₁≤θ₀≤ θ₂ la partícula desliza hacia arriba, la velocidad angular es positiva dθ/dt>0. Las fuerzas sobre la partícula se muestran en la figura.

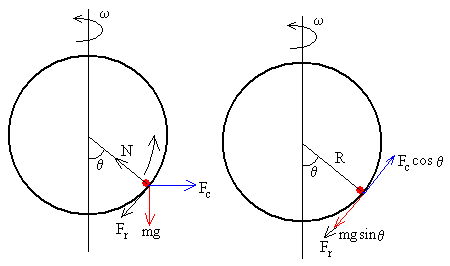
La ecuación del movimiento es

$\begin{array}{l} m R \frac{d^{2} θ}{d t^{2}} = F_{c} \cos θ - m g \sin θ - F_{r} \\ \frac{d^{2} θ}{d t^{2}} = (ω^{2} \cos θ - \frac{g}{R}) \sin θ - μ (ω^{2} \sin^{2} θ + \frac{g}{R} \cos θ) \end{array}$

Cuando la partícula se detiene se verifica si |F_r/N|<μ en cuyo caso la partícula permanece en reposo, en caso contrario, continua su movimiento hasta la próxima posición de parada.

Los ángulos límites θ₁y θ₂o θ₃para un valor dado del coeficiente de rozamiento μ y una determinada velocidad angular ω se pueden calcular aplicando el procedimiento numérico del punto medio para resolver la ecuación trascendente. F_r=μN

|gsinθ-ω²Rsinθcosθ|=μ(gcosθ+ω²Rsin²θ)

Actividades

Se introduce

La posición angular inicial θ₀, actuando en la barra de desplazamiento titulada Posición angular.
La velocidad angular de rotación ω, en el control de edición titulado V. angular.
El coeficiente de rozamiento μ, actuando en la barra de desplazamiento titulada Coef. rozamiento.
El radio de la pista circular se ha fijado en R=1.0 m

Se pulsa el botón titulado Empieza

Observamos el movimiento de la partícula en equlibrio o deslizando a lo largo de la pista circular, tal como lo vería un observador no inercial que girase con la pista circular. Se marca la posición angular de equilibrio estable θ_e.

En la parte derecha del applet, se representa la curva de energía potencial E_p(θ) en color azul, la energía total E (un segmento de color negro). La partícula oscila alrededor de las posiciones de equilibrio θ_e entre las posiciones de retorno, una es la posición inicial θ₀ y la otra la raíz de la ecuación E_p(θ)=E_p(θ₀).

stokesApplet aparecerá en un explorador compatible con JDK 1.1.