Un superficie cónica que gira

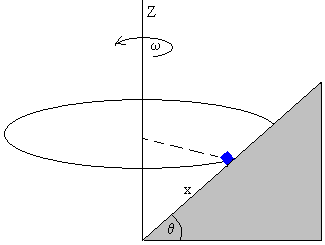
Una superficie cónica, que forma un ángulo θ con la horizontal está girando alrededor de su eje vertical Z con velocidad angular constante ω.

Sobre la superficie hay un cuerpo de masa m situado a una distancia x medida desde el vértice del cono en el que hemos puesto el origen O.

El coeficiente de rozamiento entre el cuerpo y la superficie cónica es μ. Vamos a estudiar en esta página el movimiento del cuerpo para distintas posiciones y velocidades angulares de rotación.

Rozamiento nulo

Consideremos primero el caso más sencillo, cuando no hay rozamiento entre el cuerpo y la superficie sobre la que desliza.

Sistema de referencia inercial

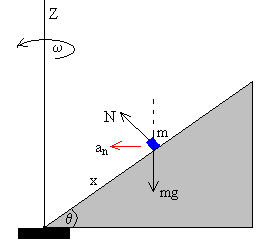
Sobre el cuerpo actúan las siguientes fuerzas:

El peso mg
La reacción N de la superficie cónica.

El cuerpo describe una trayectoria circular centrada en el eje Z de radio x·cosθ. La aceleración normal a_n=ω² x·cosθ tiene dirección radial y sentido hacia el centro de la circunferencia.

Descomponemos la reacción N y aplicamos:

Equilibrio en la dirección vertical, perpendicular al plano de la trayectoria circular

Ncosθ=mg

La ecuación de la dinámica del movimiento circular uniforme en la dirección radial

Nsinθ=mω² x·cosθ

Eliminando N en el sistema de dos ecuaciones, la posición de equilibrio es

$x_{e} = \frac{g}{ω^{2}} \frac{\sin θ}{\cos^{2} θ}$

Sistema de referencia no inercial

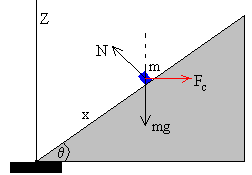
Si el observador está situado sobre la superficie cónica que gira con velocidad angular ω verá el cuerpo en equilibrio, bajo la acción de las siguientes fuerzas:

El peso mg
La reacción N de la superficie cónica.
La fuerza centrífuga, F_c= mω²x·cosθ

Descomponemos la reacción N, y aplicamos las condiciones de equilibrio

Ncosθ=mg
Nsinθ=mω² x·cosθ

Obtenemos las mismas ecuaciones que en el apartado anterior

Estabilidad de las soluciones

El peso es una fuerza conservativa. Situamos el nivel cero de energía potencial en el vértice de la superficie cónica

E_g= mgx·sinθ

La fuerza centrífuga depende solamente de la distancia r al eje de rotación, es una fuerza conservativa similar a la que ejerce de un muelle elástico.

La fuerza que ejerce un muelle elástico tiene sentido contrario al desplazamiento F=-kx, su energía potencial es positiva E_p=kx²/2

La fuerza centrífuga tiene el mismo sentido que el desplazamiento F=mω²·r

$\begin{array}{l} \int_{0}^{r} m ω^{2} r \cdot d r = 0 - E_{p} \\ E_{c} = - \frac{1}{2} m ω^{2} r^{2} = - \frac{1}{2} m ω^{2} x^{2} \cos^{2} θ \end{array}$

y su energía potencial será por tanto negativa. La energía potencial inicial para r=0, se toma como cero.

Cuando el cuerpo se encuentra en la posición x sobre la superficie cónica, la energía potencial total será la suma de ambas contribuciones E_p=E_g+E_c.

$E_{p} (x) = m g x \sin θ - \frac{1}{2} m ω^{2} x^{2} \cos^{2} θ$

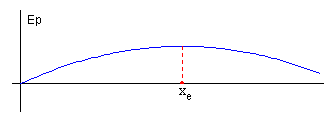
La condición de equilibrio x_e se establece cuando E_p sea un extremo (máximo o mínimo)

$\begin{array}{l} \frac{d E_{p}}{d x} = m g \sin θ - m ω^{2} x \cdot \cos^{2} θ = 0 \\ x_{e} = \frac{g}{ω^{2}} \frac{\sin θ}{\cos^{2} θ} \end{array}$

La estabilidad de la solución depende de la derivada segunda.

$\frac{d^{2} E_{p}}{d x^{2}} = - m ω^{2} \cos^{2} θ < 0$

La energía potencial presenta un máximo para x_e, la derivada segunda es negativa y el equilibrio es inestable.

Si se coloca el cuerpo en la posición x>x_e desliza hacia arriba
Si se coloca el cuerpo en la posición x<x_e desliza hacia el vértice de la superficie cónica.

Rozamiento no nulo

Describiremos el movimiento del cuerpo desde el punto de vista del observador no inercial situado sobre la superficie cónica.

Supongamos que el cuerpo se coloca en una posición x>x_e, el cuerpo tenderá a deslizar hacia arriba, la fuerza de rozamiento se opondrá a este deslizamiento. Las fuerzas sobre el cuerpo serán:

El peso mg
La reacción N de la superficie cónica.
La fuerza centrífuga, F_c= mω² x·cosθ
La fuerza de rozamiento, F_r.

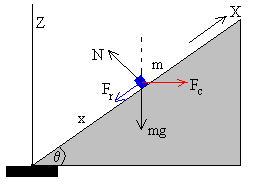
Descomponemos las fuerzas a lo largo del plano y perpendicularmente al plano inclinado.

Si el cuerpo se encuentra en equilibrio entonces,

F_c·cosθ=mg·sinθ+F_r
N=mg·cosθ+F_c·sinθ

Cuando la fuerza de rozamiento alcance su valor máximo F_r=μN el cuerpo empezará a deslizar hacia arriba a lo largo de la superficie cónica.

$\begin{array}{l} m ω^{2} x \cos^{2} θ = m g \sin θ + μ (m g \cos θ + m ω^{2} x \cos θ \sin θ) \\ x_{1} = \frac{g}{ω^{2}} \frac{\sin θ + μ \cos θ}{\cos θ - μ \sin θ} \frac{1}{\cos θ} \end{array}$

Cuando la posición inicial del cuerpo x₀≥x₁ el cuerpo desliza hacia arriba, calculamos su aceleración

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = m ω^{2} x \cos^{2} θ - m g \sin θ - μ (m g \cos θ + m ω^{2} x \cos θ \sin θ) \\ \frac{d^{2} x}{d t^{2}} - ω^{2} (\cos θ - μ \sin θ) \cos θ \cdot x = - g (\sin θ + μ \cos θ) \\ \frac{d^{2} x}{d t^{2}} - k_{1}^{2} \cdot x = - c_{1} \end{array}$

La solución de esta ecuación diferencial es

$\begin{array}{l} x = \frac{c_{1}}{k_{1}^{2}} + A \exp (- k_{1} t) + B \exp (k_{1} t) \\ \frac{d x}{d t} = - k_{1} A \exp (- k_{1} t) + k_{1} B \exp (k_{1} t) \end{array}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, la posición inicial x=x₀ y la velocidad inicial dx/dt=0, parte del reposo.

$x = \frac{c_{1}}{k_{1}^{2}} + (x_{0} - \frac{c_{1}}{k_{1}^{2}}) \cosh (k_{1} t)$

Supongamos que el cuerpo se coloca en una posición x<x_e, el cuerpo tenderá a deslizar hacia abajo hacia el vértice de la superficie cónica, la fuerza de rozamiento se opondrá a este deslizamiento. Las fuerzas sobre el cuerpo serán.

El peso mg
La reacción N de la superficie cónica.
La fuerza centrífuga, F_c= mω² x·cosθ
La fuerza de rozamiento, F_r.

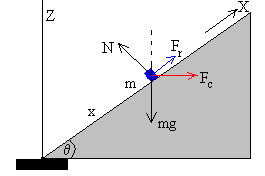
Descomponemos las fuerzas a lo largo del plano y perpendicularmente al plano

Si el cuerpo se encuentra en equilibrio entonces,

mg·sinθ=F_c·cosθ +F_r
N=mg·cosθ+F_c·sinθ

Cuando la fuerza de rozamiento alcance su valor máximo F_r=μN el cuerpo empezará a deslizar hacia abajo a lo largo de la superficie cónica.

$\begin{array}{l} m g \sin θ = m ω^{2} x \cos^{2} θ + μ (m g \cos θ + m ω^{2} x \cos θ \sin θ) \\ x_{2} = \frac{g}{ω^{2}} \frac{\sin θ - μ \cos θ}{\cos θ + μ \sin θ} \frac{1}{\cos θ} \end{array}$

Cuando la posición inicial del cuerpo x₀≤x₂ el cuerpo desliza hacia abajo, calculamos su aceleración.

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = m ω^{2} x \cos^{2} θ - m g \sin θ + μ (m g \cos θ + m ω^{2} x \cos θ \sin θ) \\ \frac{d^{2} x}{d t^{2}} - ω^{2} (\cos θ + μ \sin θ) \cos θ \cdot x = - g (\sin θ - μ \cos θ) \\ \frac{d^{2} x}{d t^{2}} - k_{2}^{2} \cdot x = - c_{2} \end{array}$

La solución de esta ecuación diferencial es

$\begin{array}{l} x = \frac{c_{2}}{k_{2}^{2}} + A \exp (- k_{2} t) + B \exp (k_{2} t) \\ \frac{d x}{d t} = - k_{2} A \exp (- k_{2} t) + k_{2} B \exp (k_{2} t) \end{array}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, la posición inicial x=x₀ y la velocidad inicial dx/dt=0, parte del reposo.

$x = \frac{c_{2}}{k_{2}^{2}} + (x_{0} - \frac{c_{2}}{k_{2}^{2}}) \cosh (k_{2} t)$

Si sinθ>μcosθ, o bien, si tanθ>μ, el cuerpo permanecerá en equilibrio en el intervalo x₂<x<x₁,
Si sinθ<μcosθ, o bien, si tanθ<μ, entonces x₂<0 lo que no tiene sentido físico. El cuerpo permanecerá en equilibrio en el intervalo 0<x<x₁.

Ejemplo:

El coeficiente de rozamiento, μ=0.2.
La velocidad angular de rotación, ω=7 rad/s
El ángulo que forma la superficie cónica con la horizontal, θ=30º

Cuando no hay rozamiento la posición de equilibrio inestable es

$x_{e} = \frac{g}{ω^{2}} \frac{\sin θ}{\cos^{2} θ} x_{e} = \frac{9.8}{7^{2}} \frac{\sin 30}{\cos^{2} 30} = 13.33 cm$

Cuando hay rozamiento

La partícula está en equilibrio entre las posiciones x₂ y x₁

$\begin{array}{l} x_{1} = \frac{g}{ω^{2}} \frac{\sin θ + μ \cos θ}{\cos θ - μ \sin θ} \frac{1}{\cos θ} x_{1} = \frac{9.8}{7^{2}} \frac{\sin 30 + 0.2 \cos 30}{\cos 30 - 0.2 \sin 30} \frac{1}{\cos 30} = 20.3 cm \\ x_{2} = \frac{g}{ω^{2}} \frac{\sin θ - μ \cos θ}{\cos θ + μ \sin θ} \frac{1}{\cos θ} x_{2} = \frac{9.8}{7^{2}} \frac{\sin 30 - 0.2 \cos 30}{\cos 30 + 0.2 \sin 30} \frac{1}{\cos 30} = 7.8 cm \end{array}$

Cuando la posición inicial del cuerpo es x₀<x₂ desliza hacia abajo
Cuando la posición inicial del cuerpo es x₀>x₁ desliza hacia arriba.

Actividades

Se introduce

La posición inicial x₀, actuando en la barra de desplazamiento titulada Posición.
La velocidad angular de rotación ω, en el control de edición titulado V. angular.
El coeficiente de rozamiento μ, actuando en la barra de desplazamiento titulada Coef. rozamiento.
El ángulo que forma la superficie cónica con la horizontal se ha fijado en θ=30º
Se pulsa el botón titulado Empieza

Observamos el movimiento de cuerpo deslizando sobre la superficie cónica, tal como lo vería un observador no inercial que girase con la pista. Se marca la posición angular de equilibrio inestable x_e.

En la parte derecha del applet, se representa la curva de energía potencial E_p(x) en color azul, que como vemos presenta un máximo en la posición de equilibrio inestable.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.