Movimiento sobre una superficie cóncava en forma de cicloide

Movimiento a lo largo de un camino recto

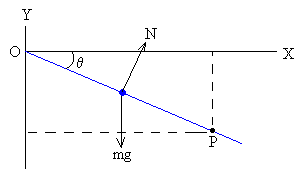
Supongamos un camino recto que une el origen (0.0) y el punto P (x_p, y_p)

Como vemos en la figura, las fuerzas sobre la partícula de masa m son:

el peso mg
la reacción de la superficie N

La fuerza neta sobre la partícula es mg·sin|θ|, la aceleración es constante. Las ecuaciones del movimiento son

$\begin{array}{l} v = g \cdot \sin | θ | t s = \frac{1}{2} g \sin | θ | \cdot t^{2} \\ \tan θ = \frac{y_{p}}{x_{p}} \end{array}$

La posición (x, y) del móvil en función del tiempo es

x=s·cosθ, y=s·sinθ

El tiempo que tarda en llegar al punto P, partiendo del origen, en reposo, es

$\sin θ = \frac{y_{p}}{s} s = \sqrt{x_{p}^{2} + y_{p}^{2}} t = \sqrt{2 \frac{x_{p}^{2} + y_{p}^{2}}{g | y_{p} |}}$

Movimiento a lo largo de una cicloide

Establecemos el mismo origen y ejes para describir el movimiento sobre la cicloide

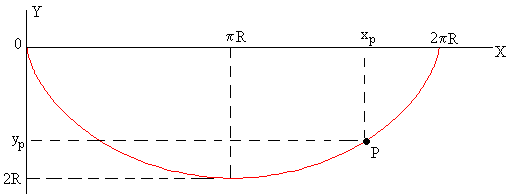
La ecuación de la cicloide de la figura es

x=R(φ-sinφ)
y=-R(1-cosφ)

Cuando φ=0, x=0, y=0, cuando φ=π, x=πR, y=-2R, cuando φ=2π, x=2πR, y=0

Si la cicloide pasa por el punto P (x_p, y_p)

x_p=R(φ-sinφ)
y_p=-R(1-cosφ)

Dividiendo ambas ecuaciones, obtenemos una ecuación trascendente en φ, que resolvemos por procedimientos numéricos

$\frac{x_{p}}{y_{p}} = - \frac{ϕ - \sin ϕ}{1 - \cos ϕ}$ (1)

Una vez que tenemos el valor de φ, se calcula el parámetro R, en cualquiera de las dos ecuaciones

La cicloide es simétrica, por lo que situamos el eje Y’ como eje de simetría, y el origen en la parte más baja de la curva, tal como se muestra en la figura. La ecuación de la cicloide referida a estos ejes es

x’=R(2θ+sin(2θ))
y’=R(1-cos(2θ))

donde θ es la pendiente de la recta tangente a la cicloide en el punto x'

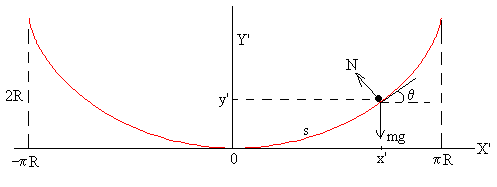
Sobre la partícula actúan dos fuerzas: el peso mg y la reacción de la superficie N. La ecuación del movimiento en la dirección tangencial es

$m \frac{d^{2} s}{d t^{2}} = - m g \sin θ \frac{d^{2} s}{d t^{2}} + \frac{g}{4 R} s = 0$

La partícula describe un Movimiento Armónico Simple (MAS) de frecuencia angular ω, y periodo P

$ω^{2} = \frac{g}{4 R} P = 2 π \sqrt{\frac{4 R}{g}}$

Si la partícula parte en el instante t=0, del extremo izquierdo (-πR, 2R) con velocidad inicial nula. La ecuación del movimiento es

s=-4R·cos(ωt)

Siendo s la posición de la partícula a lo largo del camino en forma de cicloide. La velocidad de la partícula es

$v = \frac{d s}{d t} = 4 R ω \cdot \sin (ω t)$

Las posiciones x’ e y’ de la partícula en función del tiempo t se calculan del siguiente modo:

Dada la longitud del arco s se calcula la pendiente de la recta tangente θ. Conocido el parámetro θ, se calcula x’ e y’ mediante las ecuaciones de la cicloide

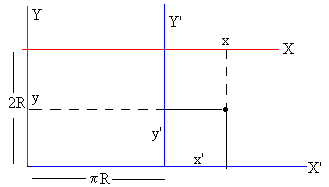
$\begin{array}{l} \sin θ = \frac{s}{4 R} \\ x' = R (2 θ + \sin (2 θ)) y' = R (1 - \cos (2 θ)) \end{array}$

Trasladamos el sistema de ejes al extremo izquierdo de la cicloide

$\begin{array}{l} x = π R + x' = π R + R (2 θ + \sin (2 θ)) = R (2 θ + π + \sin (2 θ)) \\ y = - 2 R + y' = - R (1 + \cos (2 θ)) \end{array}$

Haciendo el cambio de parámetro 2θ+π=φ, tenemos de nuevo, las ecuaciones de la cicloide referidas a los ejes X e Y

x=R(φ-sinφ)
y=-R(1-cosφ)

Balance energético

De la partícula que se mueve a lo largo del camino recto

La partícula se encuentra inicialmente en reposo en el origen, su energía total es cero E=0.

Cuando se encuentra a una altura y por debajo del origen, la partícula tiene una energía

$\begin{array}{l} E_{k} = \frac{1}{2} m v^{2} = \frac{1}{2} m {(g \sin θ)}^{2} t^{2} = \frac{1}{2} m g^{2} \sin^{2} θ \cdot t^{2} \\ E_{p} = m g y = m g s \cdot \sin θ = m g \frac{1}{2} g \sin | θ | \cdot t^{2} \cdot \sin θ = - \frac{1}{2} m g^{2} \sin^{2} θ \cdot t^{2} \end{array}$

La suma de la energía cinética y potencial es igual a la energía inicial E_p+E_k=0

De la partícula que se mueve a lo largo del camino en forma de cicloide

La partícula se encuentra en inicialmente reposo en el origen, su energía total es cero E=0.

Cuando se encuentra a una altura y por debajo del origen, la partícula tiene una energía

$\begin{array}{l} E_{k} = \frac{1}{2} m v^{2} = \frac{1}{2} m {(4 R ω \cdot sin (ω t))}^{2} = 2 m g R \sin^{2} (ω t) \\ E_{p} = m g y = m g (- 2 R + R (1 - \cos (2 θ)) = - 2 m g R \cos^{2} θ = - 2 m g R (1 - \frac{s^{2}}{16 R^{2}}) = - 2 m g R \cdot \sin^{2} (ω t) \end{array}$

La suma de la energía cinética y potencial es es igual a la energía inicial E_p+E_k=0

Ejemplo

Consideremos la recta y la cicloide que pasan por el punto (9.0, -4.5). Calcular la posición de los dos móviles en el instante t=1.5 s

El parámetro R de la cicloide se calcula resolviendo la ecuación trascendente (1) por procedimientos numéricos y vale R=2.323 m

El desplazamiento s de la partícula a lo largo de la recta inclinada un ángulo θ es

$\begin{array}{l} \tan θ = \frac{- 4.5}{9.0} θ = - 26.6 s = \frac{1}{2} 9.8 \cdot \sin 26 .6 \cdot {1.5}^{2} = 4 .93 m \\ x = s \cdot \cos θ = 4.41 m y = s \cdot \sin θ = - 2.21 m \end{array}$

La partícula que se mueve a lo largo de la cicloide, describe un MAS de frecuencia angular tal que $ω^{2} = \frac{g}{4 R}$ , ω=1.03 s^-1

El desplazamiento s de la partícula en el instante t=1.5 es

s=-4·2.323·cos(1.03·1.5)=-0.28 m, referida al sistema de ejes X’, Y’ con origen en la parte más baja de la trayectoria.

El valor del parámetro θ, que corresponde a este desplazamiento es tal que $sin θ = \frac{s}{4R}$

θ=-0.03 rad

Calculamos las coordenadas x’ e y’, y a continuación, hacemos la traslación de ejes, para determinar la posición (x, y) de la partícula

x=π·2.323+2.323(2θ+sin(2θ))=7.02 m
y=-2·2.323+2.323(1-cos(2θ))=-4.64 m

Actividades

Se pulsa el botón titulado Inicio

Se mueve con el puntero del ratón el punto de color negro intersección entre la curva cicloide y la recta, hasta la posición deseada.

Se pulsa el botón titulado Empieza

En la parte inferior izquierda, el programa nos proporciona el valor del parámetro R cuando, se elige el punto de intersección (x_p, y_p).

Observamos el movimiento de la partícula de color azul a lo largo del camino recto, y de la partícula de color rojo a lo largo del camino en forma de cicloide. La partícula de color rojo, adelanta a la de color azul, llegando antes al punto de intersección.

En cualquier momento, se puede parar la animación pulsando el botón titulado Pausa, y acercamos al instante deseado pulsando repetidamente el botón titulado Paso.

CinemaApplet1 aparecerá en un explorador compatible con JDK 1.1.