• Inicio
• Dinámica
• Trabajo y energía

La braquistrocrona

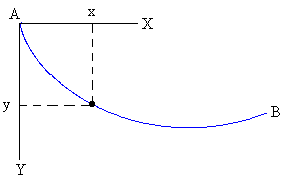Consideremos que un cuerpo desliza sin rozamiento bajando por un tobogán que tiene la forma de la curva de la figura.

Aplicando el principio de conservación de la energía, obtenemos la velocidad v del cuerpo cuando ha descendido una altura y

${\displaystyle \frac{1}{2}m{v}^2=mgy}$

El tiempo que tarda la partícula en recorrer un arco infinitesimal ds en dicha posición es

${\displaystyle dt=\frac{ds}{\sqrt{2gy}}}$

Tenemos que buscar la forma del tobogán de manera que el tiempo total que emplea la partícula en desplazarse desde A hasta B sea mínimo. Por tanto, es preciso hacer mínima la integral

${\displaystyle {\displaystyle \underset{A}{\overset{B}{\int }}\frac{ds}{\sqrt{2gy}}}}$

Teniendo en cuenta que ds²=dx²+dy², la integral se escribe en función de x e y y sus derivadas.

${\displaystyle {\displaystyle \underset{A}{\overset{B}{\int }}\frac{\sqrt{1+{\left(\frac{dx}{dy}\right)}^2}}{\sqrt{2gy}}}dy}$

Empleando el procedimiento de Euler, y teniendo en cuenta que el integrando no es función de x, la solución es

 ${\displaystyle \frac{1}{\sqrt{y}}\frac{\frac{dx}{dy}}{\sqrt{1+{\left(\frac{dx}{dy}\right)}^2}}=C\frac{dx}{dy}=\frac{C\sqrt{y}}{\sqrt{1-C^{2}y}}}$

Integrando respecto de y

${\displaystyle x={\displaystyle \underset{0}{\overset{y}{\int }}\frac{C\sqrt{y}}{\sqrt{1-C^{2}y}}}dy}$

Esta integral se resuelve haciendo la sustitución

${\displaystyle y=\frac{1}{2C^2}\left(1-\cos (2\theta )\right)}$

con lo que se obtiene

${\displaystyle x=\frac{1}{2C^2}\left(2\theta -\sin (2\theta )\right)}$

que son de nuevo las ecuaciones paramétricas de una cicloide.

Referencia

Puig Adam P., Ecuaciones diferenciales aplicado a la Física y Técnica. Biblioteca Matemática, (1970), págs. 324-325.

Curso Interactivo de Física en Internet © Ángel Franco García