Movimiento sobre una superficie cóncava en forma de cicloide

La cicloide tiene una larga historia ligada al problema de hallar la forma que debe tener un camino que una dos puntos fijos A y B para que una partícula emplee un tiempo mínimo en recorrerlo. El camino más corto es el segmento de la recta que pasa por los puntos A y B, pero el tiempo no depende solo de la longitud del camino sino también de la velocidad de la partícula.

Galileo pensó que el camino debería tener la forma de un arco de circunferencia . Pero los hermanos Bernoulli a principios del siglo XVIII demostraron que el camino debería tener la forma de un arco de cicloide. Desde ese momento, la cicloide recibió el nombre de braquistrocrona (palabra griega derivada de tiempo y mínimo).

Las demostraciones de Bernoulli dieron origen algunos años más tarde a una nueva rama de las Matemáticas, el Cálculo Variacional (Euler y después Lagrange formularían las ecuaciones básicas del cálculo de variaciones), que se encarga de buscar las funciones que cumplen que una determinada magnitud sea máxima o mínima.

En estas páginas, vamos a comparar el movimiento de una partícula a lo largo de un camino que une el origen O y un punto P, en dos casos

Cuando el camino es una línea recta.
Cuando el camino es una cicloide.
Posteriormente, esturiremos una situación más complicada, el movimiento de una partícula sobre una cicloide que presenta rozamiento.

La curva cicloide

La cicloide se produce cuando se hace rodar sin deslizar un disco sobre una superficie horizontal. Un punto del borde del disco describe una curva que se denomina cicloide (palabra griega que significa circular). A un giro del disco le corresponde un arco de la cicloide

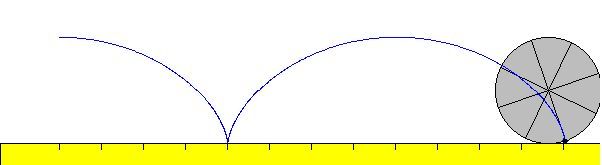
Si el punto P en el instante inicial está en la parte superior del disco, al cabo de un cierto tiempo t las coordenadas del punto P serán, tal como se muestra en la figura

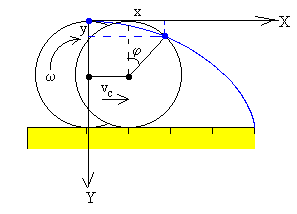x=v_c·t+R·sinφ
y=R-R·cosφ

donde R es el radio del círculo y φ el ángulo girado en el tiempo t, φ=ω·t.

La relación entre la velocidad de traslación del centro de masas v_c y de rotación ω alrededor de un eje que pasa por el centro de masa es v_c=ω ·R.

La ecuaciones paramétricas de la cicloide son

x=R(φ+sinφ)
y=R(1-cosφ )

Cuando φ=0, x=0, y=0, cuando φ=π, x=πR, y=2R, cuando φ=-π, x=-πR, y=2R,

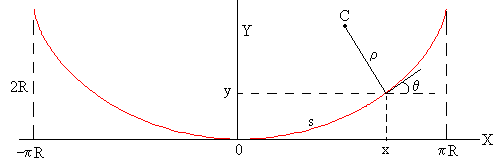
La cicloide es simétrica, por lo que situamos el eje Y como eje de simetría, y el origen en la parte más baja de la curva, tal como se muestra en la figura. La ecuación de la cicloide referida a estos ejes es

x=R(φ+sinφ)
y=R(1-cosφ)

Cuando φ=-π, x=-πR, y=2R, cuando φ=π, x=πR, y=2R,

Donde R y φ son dos parámetros

La pendiente de la cicloide en la posición x' es

$\tan θ = \frac{d y}{d x} = \frac{R \sin ϕ \cdot d ϕ}{R (1 + \cos ϕ) · d ϕ} = \frac{2 \sin (\frac{ϕ}{2}) \cos (\frac{ϕ}{2})}{2 \cos^{2} (\frac{ϕ}{2})} = \tan (\frac{ϕ}{2})$

El parámetro φ tiene un significado geométrico, φ/2 es la pendiente θ de la recta tangente a la cicloide.

Las ecuaciones paramétricas de la cicloide las podemos escribir, alternativamente

x=R(2θ+sin(2θ))
y=R(1-cos(2θ))

Calculamos ahora la longitud del arco s, entre el origen y el punto de coordenadas (x, y)

$\begin{array}{l} d s^{2} = d x^{2} + d y^{2} = (4 R^{2} {(1 + \cos (2 θ))}^{2} + 4 R^{2} \sin^{2} (2 θ)) {(d θ)}^{2} = 16 R^{2} \cos^{2} θ \cdot {(d θ)}^{2} \\ d s = 4 R \cos θ \cdot d θ \\ s = \int_{0}^{θ} 4 R \cos θ \cdot d θ = 4 R \sin θ \end{array}$

La longitud de medio arco, es decir, del arco entre el origen (0, 0) y el extremo (πR, 2R) es

$s = \int_{0}^{π / 2} 4 R \cos θ \cdot d θ = 4 R$

La trayectoria de un punto situado en el borde de una rueda de radio R que rueda sin deslizar es una cicloide. Sin embargo, el radio de curvatura de la cicloide en la posición (x, y) no es constante sino

$ρ = \frac{d s}{d θ} = 4 R \cos θ$

El radio de curvatura es máximo en el origen ρ=4R, y es mínimo en los extremos de la trayectoria ρ=0.