Dinámica de una partícula unida a una goma elástica

En otras páginas, se ha estudiado la dinámica de una partícula unida a un muelle elástico. En esta página, vamos a estudiar el movimiento de una partícula unida a una goma elástica, una situación física semejante pero que tiene una mayor riqueza de comportamientos.

Fuerza que ejerce una goma elástica

Supongamos una goma de longitud d sujeta por su extremo superior, del extremo inferior se puede colgar un cuerpo de masa m. El comportamiento de la goma es distinto al de un muelle elástico tal como podemos observar en la figura.

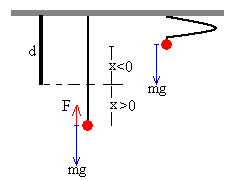
Para x<0 la goma no ejerce ninguna fuerza sobre el cuerpo de masa m. F=0
Para x>0 la goma ejerce una fuerza F=-k·x. Suponiendo que la goma tiene un comportamiento lineal (ley de Hooke)

Si sujetamos el cuerpo con la mano y hacemos que descienda muy despacio. Llega un momento en el que la fuerza que ejerce la goma equilibra el peso del cuerpo y la acción de la mano ya no es necesaria. En esta situación de equilibrio, el cuerpo se ha desplazado x_e

mg=kx_e

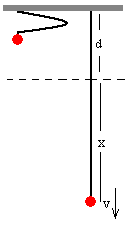Si se deja caer un cuerpo desde la posición del extremo superior de la goma x=-d, aplicando el principio de conservación de la energía podemos calcular la velocidad que alcanza cuando la goma se ha estirado una longitud x.

$\frac{1}{2} m v^{2} + \frac{1}{2} k x^{2} = m g (d + x)$

La máxima deformación x_m de la goma se alcanza cuando v=0

$\frac{1}{2} k x_{m}^{2} = m g (d + x_{m})$

A continuación, describiremos las distintas etapas del movimiento de un cuerpo unido a una goma elástica inicialmente estirada, y que presenta una mayor riqueza de comportamientos que la equivalente de un cuerpo unido a un muelle elástico.

Oscilaciones

Un cuerpo de masa m unido a un muelle elástico de constante k describe un Movimiento Armónico Simple, cuya amplitud es independiente del periodo y cuya frecuencia angular es ω²=k/m.

Supongamos que el cuerpo de masa m se desplaza hacia abajo una longitud z₀ desde la posición de equilibrio y luego se suelta (v=0), tal como se indica en la figura.

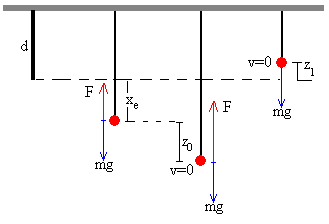
El cuerpo ascenderá impulsado por la fuerza -kx+mg. La ecuación del movimiento se escribirá

$\frac{d^{2} x}{d t^{2}} + \frac{k}{m} x = g$

La solución de esta ecuación diferencial como puede comprobarse por simple sustitución es

x=x_e +Asin(ωt)+Bcos(ωt) con ω²=k/m

Donde x_e=mg/k es la posición de equilibrio, y las constantes A y B se determinan a partir de las condiciones iniciales: en el instante t=0, x=z₀, v=dx/dt=0

La posición x del cuerpo en función del tiempo t será

x=x_e+z₀·cos(ωt)

Pueden ocurrir dos casos:

Si z₀≤x_e

El sistema describe un Movimiento Armónico Simple de amplitud z₀ y de periodo 2π/ω. El periodo de la oscilación es independiente de la amplitud z₀.

Si z₀>x_e

En el instante t=P el cuerpo llega a la posición x=0

$P = \frac{1}{ω} \arccos (- \frac{x_{e}}{z_{0}})$

con velocidad

$v_{0} = - z ω \sin (ω P) = - ω \sqrt{z_{0}^{2} - x_{e}^{2}}$

A partir de este instante, la fuerza que actúa sobre el cuerpo es su propio peso. La máxima altura que alcanza es

$z_{1} = \frac{v_{0}^{2}}{2 g}$

empleando un tiempo de Q=v₀/g

El cuerpo inicia su movimiento descendente, llegando en el instante t=P+2Q a x=0 con velocidad v₀, pero en sentido opuesto. A partir de este momento, actúa la fuerza que ejerce la goma. En el instante t= 2P+2Q vuelve a la posición de partida completándose la oscilación, cuyo periodo vale

$2 P + 2 Q = \frac{2}{ω} \arccos (- \frac{x_{e}}{z_{0}}) + \frac{2 ω}{g} \sqrt{z_{0}^{2} - x_{e}^{2}}$

La amplitud de la oscilación es

$\frac{z_{1} + x_{e} + z_{0}}{2} = \frac{1}{4 x_{e}} {(z_{0} + x_{e})}^{2}$

Aplicando el principio de conservación de la energía podemos calcular z₁

$\begin{array}{l} m g (z_{1} + x_{e} + z_{0}) = \frac{1}{2} k {(z_{0} + x_{e})}^{2} \\ z_{1} = \frac{k}{2 m g} {(x_{e} + z_{0})}^{2} - x_{e} - z_{0} = \frac{1}{2 x_{e}} {(x_{e} + z_{0})}^{2} - x_{e} - z_{0} \end{array}$

Conocido z₁ se calcula la amplitud de la oscilación (z₁+x_e+z₀)/2

Ejemplo:

Para k=400 N/m y m=350 kg.

La posición de equilibrio x_ees

$x_{e} = \frac{m g}{k} = \frac{300 \cdot 9.8}{400} = 7.35 m$

Sea la posición de partida z₀ =12.65 m (segundo caso) en el instante t=0 por debajo de la posición de equilibrio.

Empleando el principio de conservación de la emergía calculamos z₁=7.21 m la altura que se eleva el cuerpo en la región x<0.

Calculamos la frecuencia angular ω=1.15 rad/s, y el periodo de la oscilación 6.22 s que como vemos es distinto de 2π/ω, debido a que el cuerpo se mueve en la región x<0 donde la fuerza que ejerce la goma es F=0.