Condensador esférico

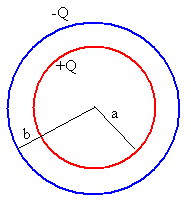Un condensador esférico está formado por dos superficies conductoras esféricas, concéntricas de radios a y b, cargadas con cargas iguales y opuestas +Q y –Q, respectivamente.

Situamos imaginariamente, una superficie esférica concéntrica de radio r, para determinar el campo eléctrico en las distintas regiones aplicando la ley de Gauss.

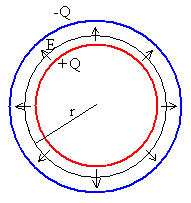Como ya se ha explicado en la página titulada “Modelo atómico de Kelvin_Thomson”, en este problema de simetría esférica, el campo eléctrico tiene dirección radial y su módulo es constante en todos los puntos de una superficie esférica de radio r. El flujo del campo eléctrico E a través de dicha superficie cerrada vale

$\oint E \cdot d S = \oint E \cdot d S \cdot \cos 0 º = E \oint d S = E \cdot 4 π r^{2}$

Determinamos la carga q encerrada en dicha superficie esférica, para distintos valores del radio r, aplicamos la ley de Gauss

$\oint E \cdot d S = \frac{q}{ε_{0}}$

Para r<a, la superficie esférica de radio r, no contiene ninguna carga, q=0, y E=0
Para a<r<b, la superficie esférica de radio r, contiene una carga, q=+Q,

$E \cdot 4 π r^{2} = \frac{Q}{ε_{0}} E = \frac{1}{4 π ε_{0}} \frac{Q}{r^{2}}$

Para r>b, la superficie esférica de radio r, contiene una carga, q=+Q-Q=0, y E=0

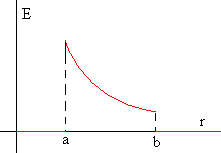En la figura, se representa el módulo del campo E en función de r.

La diferencia de potencial entre las dos placas es de radios a y b es

$V' - V = \int_{a}^{b} \frac{1}{4 π ε_{0}} \frac{Q}{r^{2}} d r = \frac{1}{4 π ε_{0}} (\frac{1}{a} - \frac{1}{b})$

La capacidad de un condensador esférico es

$C = \frac{Q}{V' - V} = \frac{4 π ε_{0}}{(1 / a - 1 / b)}$

Si el radio del segundo conductor esférico es muy grande b→∞, entonces tenemos la capacidad de un condensador esférico de radio R=a

$C = 4 π ε_{0} R$

Suponiendo que la Tierra es un conductor esférico de radio R=6370 km, su capacidad sería

$C = \frac{6370 \cdot 10^{3}}{9 \cdot 10^{9}} = 7.08 \cdot 10^{- 4} F$

Dos esferas conductoras

Sean dos esferas conductoras de radios R₁ y R₂ respectivamente, que están inicialmente aisladas una de la otra y cargadas con cargas Q₁ y Q₂ respectivamente.

Los potenciales de las superficies de las dos esferas son, respectivamente

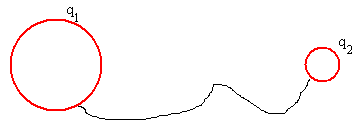
$V_{1} = \frac{1}{4 π ε_{0}} \frac{Q_{1}}{R_{1}} V_{2} = \frac{1}{4 π ε_{0}} \frac{Q_{2}}{R_{2}}$

Se ponen en contacto las dos esferas mediante un cable. La carga pasa de una esfera a la otra hasta que sus potenciales se igualan.

$\begin{array}{l} V = \frac{1}{4 π ε_{0}} \frac{q_{1}}{R_{1}} = \frac{1}{4 π ε_{0}} \frac{q_{2}}{R_{2}} \\ Q_{1} + Q_{2} = q_{1} + q_{2} \end{array}$

En este sistema de dos ecuaciones con dos incógnitas despejamos q₁ y q₂

$q_{1} = \frac{R_{1}}{R_{1} + R_{2}} (Q_{1} + Q_{2}) q_{2} = \frac{R_{2}}{R_{1} + R_{2}} (Q_{1} + Q_{2})$

El potencial común V vale

$V = \frac{Q_{1} + Q_{2}}{R_{1} + R_{2}}$