Dos esferas conductoras en un campo eléctrico uniforme
Examinamos ahora, el siguiente problema. Dos esferas conductoras del mismo radio R, inicialmente descargadas están unidas mediante un hilo conductor. Se colocan en una región en la que existe un campo eléctrico uniforme E, paralelo al eje X, tal como se muestra en la figura. El centro de la primera esfera está fijada en el origen y el centro de la segunda se desplaza a una distancia x0.
El radio de las esferas es pequeño para que el efecto de las cargas inducidas en sus superficies sea despreciable.
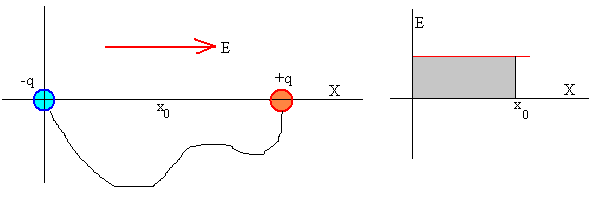
La diferencia de potencial entre las dos esferas es E·x0. Pero como están conectadas por un hilo conductor deberán estar al mismo potencial, pasará carga de la primera a la segunda esfera hasta que sus potenciales se igualen. La primera esfera se carga con una carga -q y la segunda con una carga +q.
La diferencia de potencial entre dos esferas de radio R cargadas con cargas +q y –q es
Esta diferencia de potencial debe ser igual a E·x0
Movimiento de la segunda esfera
La primera esfera está fija en el origen, la segunda esfera se coloca en la posición inicial x0 y se suelta. Observamos que esta esfera se mueve bajo la acción de dos fuerzas, la que ejerce el campo eléctrico y la fuerza de atracción entre las dos esferas.
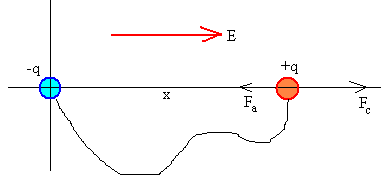
Cuando la segunda esfera está a una distancia x, la fuerza de atracción entre dos cargas puntuales +q y -q vale
que es constante
La fuerza que ejerce el campo eléctrico sobre la segunda esfera cargada con carga +q vale
La ecuación del movimiento de la segunda esfera de masa m es
La solución de esta ecuación diferencial es
Las constantes A y B se determinan a partir de las condiciones iniciales, en el instante t=0, la posición de la segunda esfera es x0 y su velocidad dx/dt=0.
La posición x y velocidad v de la segunda esfera vale
La velocidad también la podemos obtener a partir de la relación entre el trabajo de las fuerzas que actúan sobre una partícula y la variación de energía cinética.
Sustituyendo x por su expresión en función del tiempo t, podemos comprobar después de hacer algunas operaciones, que se obtiene v en función de t.
Ejemplo:
-
Intensidad del campo eléctrico, E=0.9
-
Radio de las esferas, R=0.2
-
Posición inicial, x0=5.0
-
Se ha elegido los valores de la masa m y radio R tal que el parámetro a vale a=E2
El tiempo que tarda en llegar a la posición x=15.0 es t=1.97. La velocidad en dicha posición es v=12.67..
Aproximaciones
Suponiendo que R es pequeño, el parámetro b es pequeño y por tanto, se puede despreciar la fuerza de atracción entre las esferas frente a la fuerza que ejerce el campo eléctrico externo E.
Actividades
Se introduce
-
El valor del campo E, actuando en la barra de desplazamiento titulada Campo eléctrico.
-
El radio de la esfera se ha fijado en R=0.2
-
El parámetro a se ha fijado de modo que a=E2
Se pulsa el botón titulado Nuevo
Con el puntero del ratón se arrastra la segunda esfera.
-
Cuando dicha esfera se acerca a la esfera situada en el origen, la carga pasa de la esfera derecha a la izquierda. La carga de cada esfera disminuye, así lo señala la intensidad del color azul (negativa) y rojo (positiva).
-
Cuando la esfera se aleja del origen, la carga, representada por puntos de color rojo, pasa de la esfera derecha a la esfera situada en el origen, la carga de cada esfera aumenta, así lo señala la intensidad del color azul (negativa) y rojo (positiva).
Se pulsa el botón titulado Empieza
La esfera situada en la posición x0, se mueve bajo la acción de la fuerza que ejerce el campo eléctrico y la fuerza de atracción entre las dos esferas.
A medida que la segunda esfera se aleja del origen, la carga de cada esfera aumenta.
Los datos del tiempo t y la velocidad v aparecen en la parte inferior izquierda del applet, la posición x aparece al lado de la esfera que se mueve.
Arrastre la esfera de color rojo con el puntero del ratón
Referencias
A field trip. Physics challenge for teachers and students March 2006. The Physics Teacher Vol 44