• Inicio
• Electromagnetismo
• Campos dependientes del tiempo
• Inducción mutua y autoinducción

Circuito LCR. Oscilaciones amortiguadas.

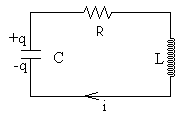
Las oscilaciones libres no se producen en un circuito real ya que todo circuito presenta una resistencia.

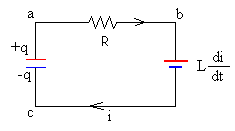En la figura de la derecha, se muestra el circuito cuando el condensador se está descargando, la carga q disminuye y la intensidad i aumenta. La fem en la bobina se opone al incremento de intensidad.

La ecuación del circuito es

${\displaystyle \begin{array}{l}{V}_{ab}+V_{bc}+V_{ca}=0\\ iR+L\frac{di}{dt}-\frac{q}{C}=0\end{array}}$

Como i=-dq/dt, ya que la carga q disminuye con el tiempo, llegamos a la siguiente ecuación diferencial de segundo orden

${\displaystyle \frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=0}$

La solución de la ecuación diferencial de las oscilaciones amortiguadas es

${\displaystyle q=Q\exp (-\gamma t)\sin \left(\omega t+\varphi \right){\omega }^{\text{2}}={\omega }_0^2-{\gamma }^2\gamma =\frac{R}{2L}}$

donde la amplitud Q y la fase inicial φ se determinan a partir de las condiciones iniciales, la carga del condensador q₀ y la intensidad de la corriente eléctrica en el circuito i₀ en el instante inicial t=0.

En las oscilaciones amortiguadas, la amplitud disminuye exponencialmente con el tiempo. La carga máxima del condensador va disminuyendo. La energía del sistema disminuye debido a que se disipa en la resistencia por efecto Joule.

Se presentan dos casos particulares:

Cuando γ =ω₀, entonces la frecuencia de la oscilación ω =0, se denomina oscilación crítica

Cuando γ >ω₀, entonces la frecuencia de la oscilación ω es un número imaginario, y se denomina oscilación sobreamortiguada.

Es fácil encontrar las relaciones que debe cumplir la capacidad C, resistencia R, y autoinducción L del circuito, para que se presenten los distintos casos de oscilación

• Amortiguadas
• Críticas
• Sobreamortiguadas

Circuito LCR conectado a un fem alterna. Oscilaciones forzadas

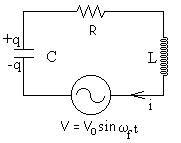
Las oscilaciones amortiguadas desaparecen al cabo de cierto tiempo, para mantener la oscilación en el circuito podemos conectarla a una fem alterna de frecuencia ω_f .

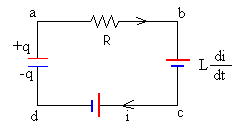La ecuación del circuito es

${\displaystyle \begin{array}{l}{V}_{ab}+V_{bc}+V_{cd}+V_{da}=0\\ iR+L\frac{di}{dt}+V_0\sin \left({\omega }_{f}t\right)-\frac{q}{C}=0\end{array}}$

Como i=-dq/dt, si la carga q disminuye con el tiempo, llegamos a la siguiente ecuación diferencial de segundo orden

${\displaystyle \frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=V_0\sin \left({\omega }_{f}t\right)}$

Ecuación similar a la estudiada para describir las oscilaciones forzadas de una masa unida a un muelle elástico.

Curso Interactivo de Física en Internet © Ángel Franco García