Distribución de las velocidades de las moléculas

Para un gas ideal monoatómico la energía de las moléculas es solamente cinética E=mv²/2.

En la fórmula (1) efectuamos el cambio de variable E por v.

$E = \frac{1}{2} m v^{2} \frac{d n}{d v} = m v \frac{d n}{d E}$

Resultando la expresión

$\frac{d n}{d v} = 4 π N {(\frac{m}{2 π k T})}^{3 / 2} v^{2} \exp (- \frac{m v^{2}}{2 k T})$ (2)

que es la fórmula de Maxwell para la distribución de velocidades de las moléculas de un gas ideal. Nos proporciona el número dn de moléculas que se mueven con una velocidad comprendida entre v y v+dv independientemente de la dirección del movimiento.

Deducción alternativa

Existe otra manera de deducir la distribución de velocidades de Maxwell

El número de moléculas cuya velocidad está comprendida entre v y v+dv, es decir entre v_x y v_x+dv_x, v_y y v_y+dv_y, v_z y v_z+dv_z, de acuerdo a la ley de Boltzmann es

$d n = c \cdot \exp (- \frac{m v^{2}}{2 k T}) d v_{x} \cdot d v_{y} \cdot d v_{z}$ (3)

donde c es una constante a determinar sabiendo que el número total de moléculas es N. Se efectúa una integral triple entre los límites -∞ y +∞,

$\begin{array}{l} d n = c \cdot \exp (- \frac{m v^{2}}{2 k T}) d v_{x} \cdot d v_{y} \cdot d v_{z} \\ N = \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} c \cdot \exp (- \frac{m v^{2}}{2 k T}) d v_{x} \cdot d v_{y} \cdot d v_{z} = c \sqrt{\frac{2 π k T}{m}} \sqrt{\frac{2 π k T}{m}} \sqrt{\frac{2 π k T}{m}} = c {(\frac{2 π k T}{m})}^{3 / 2} \end{array}$

Teniendo en cuenta el resultado de la integral

$\int_{- \infty}^{\infty} \exp (- α x^{2}) d x = \sqrt{\frac{π}{α}}$

se obtiene

$d n = N {(\frac{m}{2 π k T})}^{3 / 2} \cdot \exp (- \frac{m v^{2}}{2 k T}) d v_{x} \cdot d v_{y} \cdot d v_{z}$

Aplicaciones

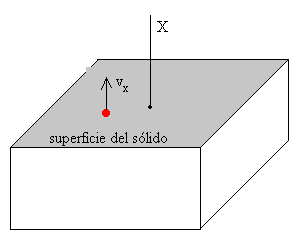maxwell_1.gif (2581 bytes) Calculamos el número de moléculas cuya componente X de la velocidad está comprendida entre v_x y v_x+dv_x independientemente de los valores de las otras dos componentes, integrando respecto de v_y y v_z entre los límites -∞ y +∞ .

$d n_{x} = N {(\frac{m}{2 π k T})}^{1 / 2} \cdot \exp (- \frac{m v_{x}^{2}}{2 k T}) d v_{x}$

La sublimación de un sólido se explica de la siguiente forma: a una temperatura T saldrán de la superficie del cristal aquellos átomos cuya componente X de la velocidad sea positiva y mayor que un valor mínimo v_min, tal que

$\frac{1}{2} m v_{\min}^{2} = φ$

donde ø es la energía de evaporación de las moléculas en la superficie del cristal

$n_{x} = N {(\frac{m}{2 π k T})}^{1 / 2} \cdot \int_{v_{\min}}^{\infty} \exp (- \frac{m v_{x}^{2}}{2 k T}) d v_{x}$

En general, el número de moléculas que tienen una componente X de su velocidad mayor que un valor mínimo se obtiene

$\begin{array}{l} n_{x} = \frac{1}{2} N (1 - erf (x)) x = \sqrt{\frac{m}{2 k T}} v_{x} \\ erf (x) = \frac{2}{\sqrt{π}} \int_{0}^{x} \exp (- z^{2}) d z \end{array}$

erf(x) se denomina función error y viene tabulada en los libros de Matemáticas. Sus valores más notables son:

erf(0)=0, y erf(∞)=1.

El efecto termoiónico es un fenómeno análogo a la sublimación de las moléculas en un sólido, aunque los electrones obedecen a la estadística cuántica de Fermi-Dirac.

El programa interactivo que viene a continuación, calcula 1-erf(x), la complementaria del de la función error cuando se introduce el valor de x en el intervalo [0, ∞).

Programa para calcular 1.0-erf(x)

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Velocidad media y velocidad cuadrática media

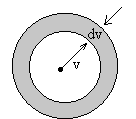En el espacio de velocidades, un elemento de volumen, es el comprendido entre dos esferas de radios v y v+dv, es decir, dv=4π v²dv, tal como se ve en la figura.

$d n = c \cdot \exp (- \frac{m v^{2}}{2 k T}) d v_{x} \cdot d v_{y} \cdot d v_{z} = c \cdot \exp (- \frac{m v^{2}}{2 k T}) 4 π v^{2} d v$

El valor de esta integral, nos permite calcular la constante de proporcionalidad c

$\int_{0}^{\infty} x^{2} \exp (- α x^{2}) d x = \frac{1}{4} \sqrt{\frac{π}{α^{3}}}$

La expresión para el número de partículas cuyo módulo de la velocidad esta comprendida entre v y v+dv es

$d n = 4 π N {(\frac{m}{2 π k T})}^{3 / 2} v^{2} \exp (- \frac{m v^{2}}{2 k T}) d v$ (2)

Que es la misma expresión (2) que hemos obtenido al comienzo de esta sección

Teniendo en cuenta los valores de las integrales

$\begin{array}{l} \int_{0}^{\infty} x^{3} \exp (- α x^{2}) d x = \frac{1}{2 α^{2}} \\ \int_{0}^{\infty} x^{4} \exp (- α x^{2}) d x = \frac{3}{8} \sqrt{\frac{π}{α^{5}}} \end{array}$

Podemos hallar la velocidad media y de la velocidad cuadrática media.

La velocidad media

$< v > = \frac{1}{N} \int_{0}^{\infty} v d n = \sqrt{\frac{8 k T}{π m}}$

La velocidad cuadrática media

$\begin{array}{l} < v^{2} > = \frac{1}{N} \int_{0}^{\infty} v^{2} d n = \frac{2}{m} < E > = \frac{3 k T}{m} \\ \frac{1}{2} m < v^{2} > = \frac{3}{2} k T \end{array}$

es la energía media de las moléculas.

La raíz cuadrada del valor medio del cuadrado de las velocidades se denomina v_rms

$v_{r m s} = \sqrt{< v^{2} >} = \sqrt{\frac{3 k T}{m}}$

A partir de la expresión (2) podemos hallar la velocidad para la cual la función de distribución presenta un máximo.

$\frac{d}{d v} (\frac{d n}{d v}) = 0 v_{m á x} = \sqrt{\frac{2 k T}{m}}$

Los datos necesarios para hallar estos valores son los siguientes

Constante de Boltzmann k=1.3805·10^-23 J/K

Número de Avogadro N_A=6.0225·10²³ /mol

Gas	Peso molecular (M) en g.
Hidrógeno (H₂)	2
Oxígeno (O₂)	32
Nitrógeno (N₂)	28
Helio (He)	4
Neón (Ne)	10
Argón (Ar)	18

Ejemplo:

Calcular la v_rms del oxígeno a 500 ºK

$v_{r m s} = \sqrt{\frac{3 \cdot 1.3805 \cdot 10^{- 23} \cdot 500}{0.032 / 6.0225 \cdot 10^{23}}} = 624.3 m/s$

Actividades

Se selecciona el gas ideal, en el control selección titulado Gas.
Se introduce la temperatura en kelvin en el control de edición titulado Temperatura.

Se pulsa en el botón titulado Gráfica.

El programa calcula la velocidad v_pa la cual la función de distribución presenta un máximo, la velocidad cuadrática media v_rms y la velocidad media <v> Representa mediante una línea vertical a trazos la velocidad cuadrática media.

Se pulsa en el botón titulado Borrar para limpiar el área de trabajo del applet.

Ejercicios:

Comparar la distribución de las velocidades de un gas ideal a distintas temperaturas
Comparar la distribución de las velocidades de varios gases ideales a la misma temperatura.