El soplo de la bomba atómica

En la madrugada del 16 de Junio de 1945 tuvo lugar en el desierto de Alamogordo (Nuevo México) la primera explosión nuclear de la historia. Mientras sus colegas del puesto de observación contemplaban el espectáculo, el físico Enrico Fermi dejó caer en el aire unos papelillos para medir su desplazamiento al llegar la onda expansiva.

Vamos a ver como a partir de la medida desplazamiento de un papelito, se puede medir la energía de la explosión de la bomba atómica.

La explosión de una bomba atómica es un fenómeno físico muy complejo, en el que interviene la liberación de una enorme cantidad de energía en forma de calor y radiación de todas las longitudes de onda. Como consecuencia, se producen procesos convectivos en el aire y la materia sólida (polvo) del suelo se levanta en la vecindad de la explosión.

En esta página, se ha elaborando un modelo simple de la explosión atómica que consta de las siguientes etapas:

En alguna decena de milisegundos una parte (el 50% aproximadamente) del total de 20 kilotones de energía liberada por fisión se deposita por radiación electromagnética en la masa de aire contenida en un volumen V₀ que es un semiesfera de radio 200 m volviéndose incandescente (la famosa bola de fuego, de color rojo). El rapidísimo calentamiento tiene lugar prácticamente a volumen constante y supondremos que de manera uniforme en todo su volumen.
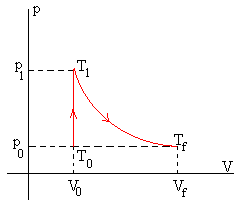
Podemos calcular la presión p₁ y la temperatura T₁ de esta bola de fuego, conocida la presión atmosférica p₀, la temperatura ambiente antes de la explosión T₀, y el volumen de aire implicado V₀. Supondremos que el aire, incluso en estas condiciones extremas se comporta como un gas ideal.
Una vez formada la bola se expande adiabáticamente en menos de un segundo hasta que su presión se iguala a la presión atmosférica, p_f=1 atm.

V_f

T_f

V_f

r_f

Esta rapidísima expansión provoca un desplazamiento del aire (onda expansiva en color azul) situado a distancias mayores que se propaga a la velocidad del sonido v_s.

El resto del fenómeno es bien conocido: por su baja densidad la bola asciende arrastrando una columna de polvo y materiales vaporizados altamente radioactivos mientras se va mezclando turbulentamente con el aire circundante. Al llegar a la tropopausa se ensancha formando el característico y terrible hongo, que luego deja su maligna siembra radiactiva en los territorios a sotavento de la explosión.

Datos necesarios para resolver el problema

1 kilotón =4.18·10¹² J
Densidad del aire a presión atmosférica y temperatura ambiente 1.0 kg/m³
Peso molecular del aire 28.9 g/mol
Temperatura ambiente antes de la explosión 17º C
Calor específico a volumen constante de los gases diatómicos c_v=5R/2
Constante R de los gases perfectos R=0.082 atm·l/(K·mol)=8.315 J/(K mol)
Velocidad del sonido v_s=330 m/s

Descripción

Calor recibido o perdido por un cuerpo: Q=m·c·(T_f-T_i). Donde m es la masa (o el número de moles), c el calor específico, T_f es la temperatura final, y T_i la inicial

Transformación adiabática: pV^γ =cte

Primera etapa. Calentamiento a volumen constante

El 50% de los 20 kilotones es la energía que calienta al aire contenido en la semiesfera de radio r=200 m

Q=0.50·20·4.18·10¹²=4.18·10¹³ J

El volumen de dicha semiesfera es $V_{0} = \frac{1}{2} \cdot \frac{4}{3} π r^{3} = \frac{16}{3} π \cdot 10^{9} l$

Masa de aire contenida en dicha semiesfera $m = ρ_{0} V_{0} = \frac{16}{3} π \cdot 10^{9} g$

En un proceso a volumen constante Q=m·c_v·(T₁-T₀)

Si la temperatura ambiente antes de la explosión era de T₀=17 ºC=290 K, después de la explosión es

$4.18 \cdot 10^{13} = \frac{16}{3} π \cdot 10^{9} \cdot \frac{5}{2} \frac{8.315}{28.9} (T_{1} - 290) T_{1} = 3758 K$

De la ecuación de los gases ideales, obtenemos la presión final

p₁·V₀=nR·T₁

El número de moles n es el cociente entre la masa y el peso molecular n=m/28.9, tomamos R=0.082 para que la presión p se mida en atm.

p₁=10.7 atm.

Segunda etapa. Expansión adiabática

$p_{1} V_{0}^{γ} = p_{0} V_{f}^{γ}$

donde γ es el índice adiabático de un gas ideal.

$γ = \frac{c_{p}}{c_{v}} = \frac{c_{v} + R}{c_{v}} = \frac{7}{5}$

Para un gas ideal diatómico γ =7/5.

De la ecuación de la transformación adiabática despejamos el volumen final V_f.

V_f=9.09·10¹⁰ litros

Este volumen corresponde a una semiesfera de radio

r_f=351.4 m.

La temperatura final del aire después de la expansión adiabática, se obtiene aplicando la ecuación de los gases ideales p₀·V_f=nR·T_f

T_f=1911 K

Tercera etapa. Propagación de la onda de choque

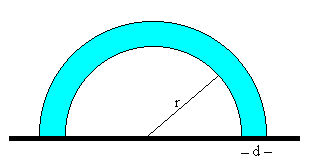bomba2.gif (1982 bytes) La capa semiesférica V_f-V₀ origina una onda de choque que se propagará radialmente a la velocidad del sonido. A medida que aumenta el radio r, la capa será cada vez más estrecha.

A una distancia r del centro de la explosión, la anchura d de la capa será.

$V_{f} - V_{0} = \frac{1}{2} \cdot \frac{4}{3} π {(r + d)}^{3} - \frac{1}{2} \cdot \frac{4}{3} π r^{3}$

Por ejemplo, si r=10 km, el valor de d será

d=0.12 m

El tiempo t que tarda en llegar los efectos de la explosión al observador será t=r/v_s, donde v_s es la velocidad del sonido. Aproximadamente, t=30.3 s.

Actividades

Se introducen los siguientes datos

La posición del observador, un número entre 5 y 20 km
La energía de la explosión un número entre 10 y 50 kilotones

Se pulsa el botón titulado Empieza.

Observamos la primera etapa, el calentamiento de la región semiesférica de 200 m de radio.

A continuación, se observa la expansión adiabática del aire contenido en dicha esfera

Aparece sobreimpreso al fenómeno, la representación gráfica de la transformación adiabática, la presión inicial y la temperatura inicial, la presión final y la temperatura final,

Una vez que se ha expandido, se observa la propagación de una capa esférica de color azul con velocidad igual a la del sonido. La capa se hace cada vez más estrecha a medida que se aleja del centro de la explosión.

Pulsando en le botón titulado Observador, nos situamos en la posición del observador y podemos medir la anchura de la capa mediante una regla. Unos puntos de color rojo representan los papelitos que han sido desplazados por la onda de choque siguiendo la flecha.

Referencias

Problemas propuestos en la IX Olimpiada Española de Física. Revista Española de Física 12(3) 1998, págs 48-49.