Medida del índice adiabático de un gas (I)

Se coloca un tubo vertical de vidrio en la boca de un recipiente grande de gas de volumen V, y se cierra el recipiente con una bola esférica de acero de masa m que ajusta perfectamente al tubo de vidrio de radio r. Se desplaza la bola de su posición de equilibrio y empieza a oscilar con un periodo que podemos medir con un cronómetro. Conocido el periodo de la oscilación podemos determinar el índice adiabático del gas.

Este es en esencia, el procedimiento de Rüchardt para medir el índice adiabático de un gas. También se describe en esta página una modificación de este procedimiento.

Método de Rüchardt

Equilibrio

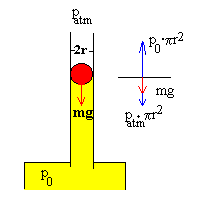Cuando la bola está en equilibrio, la presión p₀ en el recipiente es un poco más alta que la presión atmosférica, debido a la presión que ejerce la bola de masa m y radio r.

$p_{0} = p_{a t m} + \frac{m g}{π r^{2}}$

Transformación adiabática

Los cambios de presión y de volumen del gas se describen mediante un proceso termodinámico. Si suponemos que la oscilación transcurre muy rápidamente podemos considerar que el proceso es adiabático. La relación entre la presión y el volumen del gas en dicho proceso viene dada por la ecuación.

$p V^{γ} = cte$

donde V es el volumen del gas, p la presión y γ el índice adiabático del gas.

Cuando la bola se ha desplazado x de la posición de equilibrio, el volumen se ha reducido en V₀-π r²x y la presión en el recipiente ha cambiado a p, de modo que

$p_{0} V_{0}^{γ} = p {(V_{0} - π r^{2} x)}^{γ}$

Despejando p

$p = p_{0} {(1 - \frac{π r^{2} x}{V_{0}})}^{- γ}$

Dado que π r²x<< V₀. Empleando el desarrollo de Newton (a+b)ⁿ hasta el primer término

$p \approx p_{0} (1 + γ \frac{π r^{2}}{V_{0}} x)$

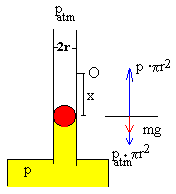La fuerza neta que actúa sobre la bola cuando se ha desplazado x de la posición de equilibrio es

F=p_atm·πr²+mg-p·πr²

$F = (p_{0} - p) π r^{2} = - p_{0} γ \frac{π^{2} r^{4}}{V_{0}} x$

La fuerza es proporcional al desplazamiento y de sentido contrario a éste, una clara indicación de que la partícula describe un M.A.S.

Oscilaciones

Cuando actuamos sobre la bola con el ratón separándola de su posición de equilibrio y soltándola, la bola comienza a oscilar.

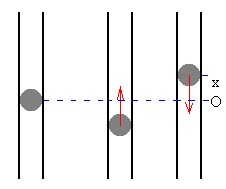En la figura vemos que, cuando la bola se desplaza hacia abajo, la presión en el recipiente aumenta, la fuerza sobre la bola está dirigida hacia arriba. Cuando la bola se desplaza hacia arriba la presión disminuye, la fuerza sobre la bola es hacia abajo. Por tanto, la fuerza sobre la bola es de sentido contrario al desplazamiento, una de las características del M.A.S.

La segunda ley de Newton en forma diferencial se escribe

$m \frac{d^{2} x}{d t^{2}} + p_{0} γ \frac{π^{2} r^{4}}{V_{0}} x = 0$

Ecuación diferencial de un Movimiento Armónico Simple (M.A.S.) de frecuencia y periodo

$ω^{2} = \frac{γ π^{2} r^{4} p_{0}}{m V_{0}} P = \frac{2 π}{ω}$

Medimos con un cronómetro el periodo P de las oscilaciones y calculamos el índice adiabático γ del gas.

$γ = \frac{4 m V_{0}}{P^{2} p_{0} r^{4}}$

Debido al rozamiento entre la bola y las paredes interiores del tubo, la amplitud de las oscilaciones no es constante, sino que disminuye con el tiempo. Por otra parte, la bola tiene un diámetro ligeramente inferior al diámetro interior del tubo, por lo que el aire circula por el hueco existente entre la bola y el tubo.

Ecuación del movimiento

La bola describe un MAS de amplitud A, frecuencia angular ω y fase inicial φ . La posición x y la velocidad v de la bola en función del tiempo t son

x=A·sin(ω t+φ )
v=dx/dt=A·ω ·cos(ω t+φ )

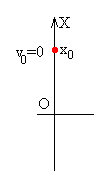La amplitud y la fase inicial se calculan a partir de las condiciones iniciales. Si en el instante inicial t=0, la bolita parte de la posición x=x₀ con velocidad nula, v=0

x₀=Asinφ
0=Aω ·cosφ

Entonces. φ =π/2 ó φ =3π /2 según que x₀>0 ó x₀<0, y A=| x₀|

En la segunda experiencia, x₀>0, de modo que la ecuación del movimiento es

x=x₀·cos(ω t)

Modificación de Rinkel

Una modificación del método de Rüchardt fue sugerida por Rinkel en 1929. Este método consiste en sostener la bola en el extremo superior del tubo y dejarla caer, determinando la altura h que recorre antes de iniciar de nuevo el movimiento hacia arriba.

Transformación adiabática

En la situación inicial, la bola se coloca en el extremo del tubo de vidrio y se mantiene sujeta con la mano. La presión del gas es la presión atmosférica p_atm y el volumen es V₀.

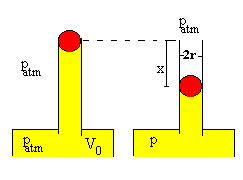Se suelta la bola y se desplaza hacia abajo x, tal como se indica en la figura. El volumen del recipiente ha disminuido en V₀-πr²·x, y la presión ha aumentado a p.

Suponiendo que la trasformación entre el estado inicial y el estado final es adiabática, tenemos la siguiente relación

$p_{a t m} V_{0}^{γ} = p \cdot {(V_{0} - π r^{2} \cdot x)}^{γ}$

Suponiendo que el volumen V₀ es muy grande respecto a los cambios de volumen del gas en el tubo. Llegamos a la siguiente relación aproximada.

$p \approx p_{a t m} (1 + γ \frac{π r^{2}}{V_{0}} x)$

Cambios energéticos

Comparemos la situación inicial con la bola en el extremo superior del tubo, con la situación en la que la bola alcanza su máximo desplazamiento recorriendo la altura h antes de iniciar el movimiento ascendente.

La velocidad inicial y la velocidad final son ambas cero, no hay cambio en la energía cinética de la bola.
La bola ha disminuido su altura. El cambio de la energía potencial es -mgh.

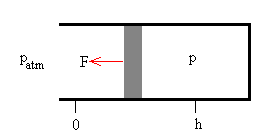El trabajo realizado por la fuerza sobre la bola debida a la diferencia de presión a ambos lados (p-p_atm) es

$W = \int_{0}^{h} - F \cdot d x = - \int_{0}^{h} (p - p_{a t m}) π r^{2} \cdot d x = - \int_{0}^{h} p_{a t m} γ \frac{π^{2} r^{4}}{V_{0}} x \cdot d x = - p_{a t m} γ \frac{π^{2} r^{4}}{2 V_{0}} h^{2}$

El trabajo es igual a la variación de energía potencial, ya que la energía cinética no cambia

W=-mgh

Llegamos finalmente a la expresión

$γ = \frac{2 m g V_{0}}{p_{a t m} π^{2} r^{4} h}$

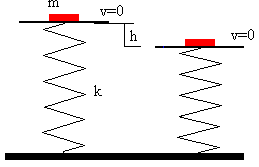Este es un ejemplo similar al de un cuerpo de masa m que se coloca sobre el extremo de un muelle elástico vertical sin deformar de constante k. Determinar la máxima deformación h del muelle.

Ejemplo:

Se necesitan para calcular el índice adiabático del gas elegido, los siguientes datos

Material de la esfera	Densidad (kg/m³)
Acero	7700
Cobre	8930
Plomo	11350
Volframio	19340

Presión atmosférica, p_atm	101300 Pa
Volumen del recipiente, V₀	10 dm³=0.01 m³

Supongamos que elegimos:

como material de la esfera el acero,
el diámetro de la esfera 16 mm
el gas del recipiente argón..

Método de Rüchardt

La masa de la bolita es

$m = 7700 \cdot \frac{4}{3} π {(0.008)}^{2} = 0.0165 kg$

La presión de equilibrio es

$p_{0} = 101300 + \frac{0.0165 \cdot 9.8}{π \cdot {(0.008)}^{2}} = 101300 + 805 = 102105 Pa$

En la escala horizontal leemos el tiempo de tres oscilaciones que es 2.98 s, el periodo de una oscilación es de P=0.99 s.

Llevamos todos los datos a la fórmula del coeficiente adiabático del gas

$γ = \frac{4 \cdot 0.0165 \cdot 0.01}{{(0.99)}^{2} \cdot 102105 \cdot {(0.008)}^{4}} = 1.61$

Pulsando en el botón titulado Respuesta obtenemos el valor 1.62.

El botón Inicio vuelve a dejar caer la bola en el extremo superior del tubo de vidrio, en disposición de volver a iniciar una nueva experiencia.

Modificación de Rinkel

Medimos el máximo desplazamiento h de la bola. Se utiliza los botones Pausa y Paso para llegar al momento en el que la bola va a iniciar su movimiento vertical ascendente.

Con los datos del ejemplo anterior y h=49 cm=0.49 m, introducimos los datos en la fórmula

$γ = \frac{2 \cdot 0.0165 \cdot 9.8 \cdot 0.01}{101300 \cdot π^{2} \cdot {0.008}^{4} \cdot 0.49} = 1.61$

Aplicamos la ecuación de la transformación adiabática

$p_{a t m} V_{0}^{γ} = p \cdot {(V_{0} - π r^{2} \cdot h)}^{γ}$

o la aproximación

$p \approx p_{a t m} (1 + γ \frac{π r^{2}}{V_{0}} h)$

para calcular la presión del gas contenido en la vasija cuando la bola ha descendido una altura h=0.49 m

p=102938 Pa

Aplicamos la ecuación de los gases ideales para calcularla temperatura T final, suponiendo una temperatura inicial de 300 K.

p_atm·V₀=nR·300
p(V₀-πr²h)=nRT

Se obtiene T=301.8 K

La variación de energía interna

$Δ U = \frac{3}{2} n R Δ T$

ΔU=9.36 J es mucho mayor que la variación de energía potencial de la bola

mgh=0.08 J

Actividades

Introducimos los siguientes datos:

El material del que está hecha la esfera
El diámetro de la bolita en mm
El gas que contiene el recipiente

Pulsamos el botón Inicio. Si el diámetro del tubo es pequeño y la "experiencia" no se puede llevar a cabo con estos datos un mensaje nos la notifica, y procederemos a cambiar los datos.

Se pulsa el botón titulado Empieza, la bolita empieza a oscilar. Podemos ver mediante flechas

El peso de la bolita en color rojo.
La resultante de las fuerzas (en color azul) que ejerce la presión del gas contenido en el recipiente y la presión atmosférica sobre la bolita.