Medida de la viscosidad de un líquido

Desplazamiento de una burbuja de aire en un tubo capilar

Se dispone horizontalmente un largo tubo de vidrio (capilar) de pequeño diámetro y longitud L. Los extremos A y B del tubo se conectan a dos recipientes grandes. Se llena el dispositivo con el líquido cuya viscosidad se desea medir de modo que una burbuja de aire permanezca en su interior del tubo horizontal.

Sea h la diferencia de las alturas entre los niveles de líquido en los dos depósitos. Cuando se abren simultáneamente las llaves en los extremos de los depósitos, la burbuja tiende a moverse a lo largo del tubo horizontal con velocidad constante v. Vamos a relacionar la diferencia de alturas h con la velocidad v con la que se desplaza de la burbuja de aire en el tubo horizontal.

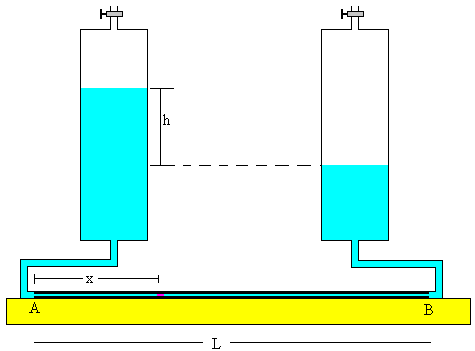
La diferencia de presión entre los extremos del tubo horizontal es

p_A-p_B=ρgh

Supongamos que la longitud del tubo es L y la longitud de la burbuja es d<<L

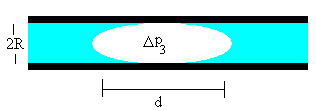
La diferencia de presión p_A-p_B cuando la burbuja está en movimiento comprende de tres partes:

Movimiento del líquido

La ley de Poiseuille afirma que el gasto G= πR²v es proporcional a la diferencia de presión. Como hay líquido en la porción L-d del tubo y el fluido se mueve con velocidad (media) v.

$Δ p_{1} = \frac{8 η (L - d)}{π R^{4}} G = \frac{8 η (L - d)}{π R^{4}} π R^{2} v = \frac{8 η (L - d)}{R^{2}} v$

Siendo η la viscosidad desconocida del fluido

Movimiento del aire de la burbuja

De modo análogo, aplicamos la ley de Poiseuille a la porción aire en el interior de la burbuja de longitud d, que se desplaza con velocidad v por el interior del tubo.

$Δ p_{2} = \frac{8 η' d}{R^{2}} v$

Siendo η’=1.72·10^-5 kg/(m·s) la viscosidad del aire

El exceso de presión en el interior de la burbuja de aire.

El exceso de presión en una burbuja esférica de radio R en el interior de un líquido de tensión superficial γ es

$Δ p_{3} = \frac{2 γ}{R}$

Cuando la burbuja no es esférica, sino de la forma mostrada en la figura, la expresión es

$Δ p_{3} = \frac{2 γ}{R} (\cos θ_{1} - \cos θ_{2})$

donde θ₁ y θ₂ son los ángulos de contacto (véase el artículo citado en las referencias).

La diferencia de presión p_A-p_B entre los extremos del tubo horizontal es

$\begin{array}{l} p_{A} - p_{B} = Δ p_{1} + Δ p_{2} + Δ p_{3} \\ ρ g h = \frac{8 v}{R^{2}} (d η' + (L - d) η) + Δ p_{3} \end{array}$

Dado que la viscosidad del aire η’ es muy pequeña, del orden de 10^-5 comparada con la viscosidad η de un líquido como el agua del orden de 10^-3 y por otra parte, la longitud de la burbuja de aire d es del orden de 1 cm frente a L que es del orden de un metro, podemos despreciar el término Δp₂ frente a las otras contribuciones.

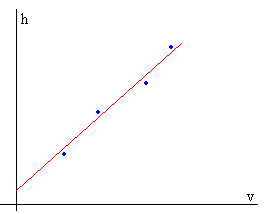$\begin{array}{l} ρ g h = \frac{8 v}{R^{2}} (L - d) η + Δ p_{3} \\ h = \frac{8 (L - d) η}{ρ g R^{2}} v + \frac{Δ p_{3}}{ρ g} \end{array}$

Cuando representamos la diferencia de presión h en cm de líquido en el eje Y y la velocidad v en cm/s en el eje X obtenemos una línea recta cuya pendiente es proporcional a la viscosidad y cuya ordenada en el origen es el exceso Δp₃/(ρg) de presión en el interior de la burbuja de aire debido a la tensión superficial del líquido.

Nota: a medida que la burbuja se desplaza en el tubo horizontal, pasa una cantidad pequeña de líquido del depósito izquierdo al derecho. Como el radio del tubo es muy pequeño y los depósitos tienen sección grande, la variación de altura es despreciable, es decir, h se mantiene prácticamente constante durante la medida.

Actividades

Se pulsa el botón titulado Inicio

Se elige el líquido en el control de selección titulado Líquido
Se establece la diferencia p_A-p_B=ρgh de presión en cm de líquido, actuando en la barra de desplazamiento titulada Presión.

Se abre la llave que permite que el aire entre en el depósito de la izquierda, y la burbuja se desplace por el capilar impulsada por la diferencia de presión entre los dos recipientes.

Se han fijado los siguientes parámetros:

El radio del tubo horizontal se ha fijado en R=0.058 cm
La longitud del tubo horizontal se ha fijado en L=100 cm
La longitud de la burbuja de aire se ha fijado en d=1 cm

Se pulsa el botón titulado Empieza

La burbuja de aire se mueve en el tubo capilar horizontal, se mide su velocidad dividiendo el desplazamiento L=100 cm entre el tiempo que tarda en desplazarse

Los pares de datos (h, v) se guardan en el control área de texto situado a la izquierda del applet.

Se pulsa el botón titulado Inicio

Se cambia la presión, es decir, la diferencia de alturas h entre niveles de líquido en los dos depósitos, y se mide la velocidad v de desplazamiento de la burbuja.

Cuando se han realizado varias medidas, se pulsa el botón titulado Gráfica

Se representa la recta

$h = \frac{8 (L - d) η}{ρ g R^{2}} v + \frac{Δ p_{3}}{ρ g}$

y los datos “experimentales” en forma de puntos.

El programa interactivo calcula la pendiente de la recta. A partir de este dato, se calcula la viscosidad η del fluido

Datos de la densidad de los líquidos

Líquido	Densidad (kg/m³)
Agua	1000
Alcohol etílico	790
Benceno	879
Anilina	1020

Ejemplo:

Elegimos el agua, después de realizar varias medidas, se pulsa el botón titulado Gráfica. La pendiente de la recta es 2.52 s

$2.52 = \frac{8 \cdot (1.0 - 0.01) \cdot η}{1000 \cdot 9.8 \cdot 0 {.00058}^{2}} η = 1.05 \cdot 10^{- 3} kg/(m·s)$

FluidoApplet1 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Elkarim A. A., A new type of viscosimeter. Am. J. Phys. 16 (9) December 1948, pp. 489-490