Método de las aproximaciones sucesivas
El método de las aproximaciones sucesivas es uno de los procedimientos más importantes y más sencillos de codificar. Supongamos la ecuación
f(x)=0
donde f(x) es una función continua que se desea determinar sus raíces reales. Se sustituye f(x) por la ecuación equivalente
x=φ(x)
Se estima el valor aproximado de la raíz x0, y se sustituye en el segundo miembro de la ecuación para obtener x1.
x1=φ(x0)
Poniendo x1 como argumento de φ(x), obtendremos un nuevo número x2, y así sucesivamente. Este proceso se puede sintetizar en la fórmula.
xn=φ(xn-1) (1)
Si esta secuencia es convergente es decir, tiende hacia un límite, la solución ξ es
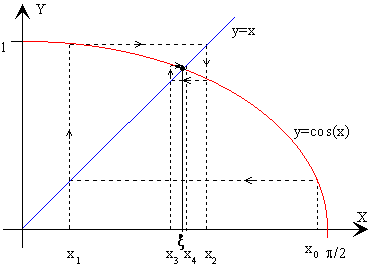
El método de iteración se explica geométricamente mediante el gráfico de la figura. Se dibuja la curva y=φ(x), y la recta y=x, bisectriz del primer cuadrante. La abscisa ξ del punto de intersección es la raíz buscada.
Un ejemplo típico es la de encontrar la raíz de la ecuación
x=cos(x)
Para encontrar la raíz, se comienza en el punto cualquiera de abscisa x0 dentro del intervalo (0, π/2), y se traza la línea vertical hasta que interseca la curva, luego, desde este punto, se traza una línea horizontal hasta que se alcanza la recta bisectriz, este punto tendrá por abscisa x1. Se traza de nuevo, una línea vertical hasta encontrar a la curva, y otra línea horizontal hasta encontrar la línea recta, el punto de intersección tiene de abscisa x2 , y así sucesivamente. Como podemos apreciar en la figura, la sucesión x1, x2, x3... tiende hacia la raíz ξ de la ecuación buscada.
Tal como nos sugiere la representación gráfica de la función en la figura, la raíz buscada está en el intervalo 0 a π/2. Tomamos una aproximación inicial a la raíz x0, en dicho intervalo y aplicamos la fórmula (1). Su codificación no presenta grandes dificultades.
double x=0.5;
while(true){
x=Math.cos(x);
}
La condición de finalización
Primero, introducimos el valor inicial x, la primera aproximación, calculamos el valor del coseno de x, el valor devuelto (segunda aproximación), lo guardamos de nuevo en la variable x, y repetimos el proceso indefinidamente. El código aunque correcto, necesita terminarse en algún momento, cumpliendo una determinada condición. Cuando el valor absoluto del cociente entre la diferencia de dos términos consecutivos de la sucesión y uno de los términos, sea menor que cierta cantidad ε.
Este criterio, no es completamente riguroso, pero es un buen punto de partida para el estudio de este método. Volvemos a escribir el código incluyendo la condición de terminación y dentro de una función denominada raiz, a la que se le pasa el valor inicial y que devuelve la raíz buscada
final double ERROR=0.001;
double raiz(double x0){
double x1;
while(true){
x1=Math.cos(x0);
if(Math.abs((x1-x0)/x1)<ERROR) break;
x0=x1;
}
return x0;
}
En primer lugar, fijamos el valor de la constante ε o ERROR. Introducimos la primera aproximación a la raíz, y la guardamos en la variable x0, calculamos su coseno y obtenemos la segunda aproximación, la guardamos en la variable x1Verificamos si se cumple la condición de terminación. En el caso de que no se cumpla, x0 toma el valor de x1 y se repite el proceso. En el momento en que se cumpla la condición de terminación, se sale del bucle y la función devuelve la raíz buscada. Como podemos observar las variables x0 y x1 guardan dos términos consecutivos de la sucesión que tiende hacia la raíz de la función.
La clase que describe el procedimiento
Queremos que el procedimiento numérico sea independiente de la función f(x) cuya raíz deseamos averiguar. Para ello, creamos una clase base abstracta denominada Ecuacion con una función miembro raiz que defina el procedimiento numérico, y que deje sin definir la función f(x), declarándola abstracta, dejando a las clases derivadas de Ecuacion la definición de la función f(x) particular.
public abstract class Ecuacion {
protected static final double ERROR=0.001;
public double raiz(double x0){
double x1;
while(true){
x1=f(x0);
if(Math.abs(x1-x0)<ERROR) break;
x0=x1;
}
return x0;
}
abstract public double f(double x);
}
|
En la clase derivada denominada Funcion se define la función f(x)
public class Funcion extends Ecuacion{
public double f(double x){
return Math.cos(x);
}
} |
Creamos un objeto de la clase derivada y llamamos desde ellos a la función raiz que describe el procedimiento numérico
public class Aplicacion {
public static void main(String[] args) {
Funcion f1=new Funcion();
System.out.println("solucion "+f1.raiz(0.5));
System.out.println("solucion1 "+f1.raiz(0.9));
}
} |
En las dos primeras llamadas a la función raiz comprobamos que la solución buscada no depende del valor inicial de partida x0, que en el primer caso es 0.5 y en el segundo caso es 0.9.
El criterio de convergencia
No todas las ecuaciones pueden resolverse por este método, solamente si el valor absoluto de la derivada de la función φ(x) en la vecindad de la raíz ξ es menor que la unidad (la pendiente de la recta bisectriz del primer cuadrante es uno). En la figura, podemos ver como es imposible encontrar la solución marcada por un puntito negro en la intersección entre la curva y la recta bisectriz del primer cuadrante, ya que la sucesión xi diverge.
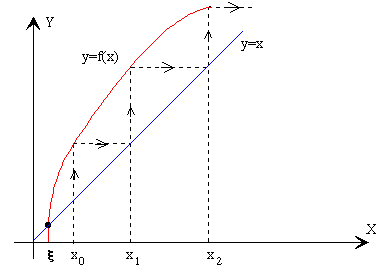
Por ejemplo, la ecuación
x3-x-1=0
tiene una raíz en el intervalo (1, 2) ya que f(1)=-1<0 y f(2)=5>0. Esta ecuación puede escribirse de la forma
x=x3-1
En este caso,
φ(x)= x3-1 y su derivada es φ'(x)= 3x2
y por tanto,
φ'(x)≥3 para 1≤x≤2
en consecuencia, no se cumplen las condiciones de convergencia del proceso de iteración. Si escribimos la ecuación en la forma
como podrá verificar fácilmente el lector, cumple las condiciones de convergencia,
obteniéndose rápidamente un valor aproximado de la raíz buscada.![]()
