• Inicio
• Métodos numéricos
• Tratamiento de pares de datos

Método de los mínimos cuadrados. Polinomio aproximador

Supongamos que hemos medido un conjunto de pares de datos (x_i, y_i) en una experiencia, por ejemplo, la posición de un móvil en ciertos instantes de tiempo.

Queremos obtener una función y=f(x) que se ajuste lo mejor posible a los valores experimentales. Se pueden ensayar muchas funciones, rectas, polinomios, funciones potenciales o logarítmicas.

Una vez establecido la función a ajustar se determinan sus parámetros, en el caso de un polinomio, serán los coeficientes del polinomio de modo que los datos experimentales se desvíen lo menos posible de la fórmula empírica.

La función más sencilla es la función lineal y=ax+b. El procedimiento de ajustar los datos experimentales a una línea recta se denomina regresión lineal

Ejemplos de polinomio aproximador:

El contador del reproductor de la casete

Polinomio aproximador

Queremos aproximar un polinomio de grado n, a un conjunto de m+1 pares de datos (x_i, y_i) de modo que n≤m.

Sea el polinomio

P(x)=a₀+a₁x+a₂x²+...a_nxⁿ

Se calcula la cantidad

${\displaystyle S={\displaystyle \sum _{i=0}^m{\left(P(x_i)-y_i\right)}^2={\displaystyle \sum _{i=0}^m{\left(a_0+a_1{x}_i+a_2{x}_i^2+\mathrm{....}+a_n{x}_i^n-y_i\right)}^2}}}$

Para obtener los valores de los coeficientes del polinomio aproximador se tienen que determinar los valores de los coeficientes a₀, a₁, a₂, ...a_n de forma que la cantidad S tome un valor mínimo.

Hagamos las derivadas parciales de S respecto de a₀, a₁, a₂, ...a_n iguales a cero

${\displaystyle \begin{array}{l}\frac{1}{2}\frac{\partial S}{\partial a_0}={\displaystyle \sum _{i=0}^m\left(a_0+a_1{x}_i+a_2{x}_i^2+\mathrm{....}{a}_n{x}_i^n-y_i\right)·1=0}\\ \frac{1}{2}\frac{\partial S}{\partial a_1}={\displaystyle \sum _{i=0}^m\left(a_0+a_1{x}_i+a_2{x}_i^2+\mathrm{....}{a}_n{x}_i^n-y_i\right)·x_i=0}\\ \mathrm{...............................................................................}\\ \frac{1}{2}\frac{\partial S}{\partial a_n}={\displaystyle \sum _{i=0}^m\left(a_0+a_1{x}_i+a_2{x}_i^2+\mathrm{....}{a}_n{x}_i^n-y_i\right)x_i^n=0}\end{array}}$              (1)

Obtenemos un sistema de n+1 ecuaciones con n+1 incógnitas, a₀, a₁, a₂, ...a_n

Ejemplo:

Supongamos que tenemos 4 pares de datos y que queremos ajustarlos al polinomio de segundo grado y=a₀+a₁x+a₂x²

Las ecuaciones (1) se escribirán

${\displaystyle \begin{array}{l}(a_0+a_1{x}_0+a_2{x}_0^2)+(a_0+a_1{x}_1+a_2{x}_1^2)+(a_0+a_1{x}_2+a_2{x}_2^2)+(a_0+a_1{x}_3+a_2{x}_3^2)-(y_0+y_1+y_2+y_3)=0\\ (a_0+a_1{x}_0+a_2{x}_0^2)x_0+(a_0+a_1{x}_1+a_2{x}_1^2)x_1+(a_0+a_1{x}_2+a_2{x}_2^2)x_2+(a_0+a_1{x}_3+a_2{x}_3^2)x_3-(y_0{x}_0+y_1{x}_1+y_2{x}_2+y_3{x}_3)=0\\ (a_0+a_1{x}_0+a_2{x}_0^2)x_0^2+(a_0+a_1{x}_1+a_2{x}_1^2)x_1^2+(a_0+a_1{x}_2+a_2{x}_2^2)x_2^2+(a_0+a_1{x}_3+a_2{x}_3^2)x_3^2-(y_0{x}_0^2+y_1{x}_1^2+y_2{x}_2^2+y_3{x}_3^2)=0\end{array}}$

agrupando términos

${\displaystyle \begin{array}{l}4a_0+(x_0+x_1+x_2+x_3)a_1+(x_0^2+x_1^2+x_2^2+x_3^2)a_2=(y_0+y_1+y_2+y_3)\\ (x_0+x_1+x_2+x_3)a_0+(x_0^2+x_1^2+x_2^2+x_3^2)a_1+(x_0^3+x_1^3+x_2^3+x_3^3)a_2=(y_0{x}_0+y_1{x}_1+y_2{x}_2+y_3{x}_3)\\ (x_0^2+x_1^2+x_2^2+x_3^2)a_0+(x_0^3+x_1^3+x_2^3+x_3^3)a_1+(x_0^4+x_1^4+x_2^4+x_3^4)a_2=(y_0{x}_0^2+y_1{x}_1^2+y_2{x}_2^4+y_3{x}_3^2)\end{array}}$

Se despeja a₀, a₁, a₂

Volvamos al sistema de n+1 ecuaciones con n+1 incógnitas. Introduzcamos las expresiones

${\displaystyle \begin{array}{l}{s}_k=x_0^k+x_1^k+x_2^k+\mathrm{...}{x}_m^k(k=\mathrm{0,}\mathrm{...}2n)\\ t_k=x_0^k{y}_0+x_1^k{y}_1+x_2^k{y}_2+\mathrm{...}{x}_m^k{y}_m(k=\mathrm{0,}\mathrm{...}n)\end{array}}$             (2)

Se obtiene el siguiente sistema de n+1 ecuaciones con n+1 incógnitas

${\displaystyle \begin{array}{l}{a}_0{s}_0+a_1{s}_1+a_2{s}_2+\mathrm{....}{a}_n{s}_n=t_0\\ a_0{s}_1+a_1{s}_2+a_2{s}_3+\mathrm{....}{a}_n{s}_{n+1}=t_1\\ a_0{s}_2+a_1{s}_3+a_2{s}_4+\mathrm{....}{a}_n{s}_{n+2}=t_2\\ \mathrm{.....................................................}\\ a_0{s}_n+a_1{s}_{n+1}+a_2{s}_{n+2}+\mathrm{....}{a}_n{s}_{2n}=t_n\end{array}}$                  (3)

Si todos los puntos son distintos, el sistema de ecuaciones tiene una solución única.

Para resolver el sistema de ecuaciones se puede emplear alguno de los varios procedimientos existentes. El método empleado en este programa es el método de iteración. Ya que la matriz del sistema de ecuaciones es positiva, para este sistema se emplea el procedimiento de Seidel.

La clase PolRegesion.

La clase PolRegresion tiene los siguientes miembros dato

public class PolRegresion {
	private double[] x; //datos
	private double[] y;
	private int nDatos;	
	double[][] m; //matriz de los coeficientes
	double[] t; //términos independientes
	public double[] a; //polinomio a[0]+a[1]·x+a[2]·x2+...
	public int grado; //grado del polinomio

El constructor inicializa los miembros, array x, array y que guardan los resultados experimentales y el número nDatos de dichos datos. El constructor crea la matriz m, el vector t, y reserva espacio para el array que va a guardar los coeficientes del polinomio a, cuyo grado se guarda en el miembro grado.

public PolRegresion(double[] x, double[] y, int grado) {
	this.x=x;
	this.y=y;
	nDatos=x.length;
	this.grado=grado;
	t=new double[grado+1];
	m=new double[grado+1][grado+1];
	a=new double[grado+1];
}

A partir de datos (x_i, y_i) se tiene que obtener la matriz m cuadrada de los coeficientes (3) de dimensión n (grado+1) y el vector t de dimensión n usando las fórmulas (2). La función miembro coeficientes calcula los elementos del vector t y de la matriz m.

private void coeficientes(){
	double[] s=new double[2*grado+1];
	double suma;
	for(int k=0; k<=2*grado; k++){
		suma=0.0;
		for(int i=0; i<nDatos; i++){
			suma+=potencia(x[i], k);
		}

		s[k]=suma;

	}

	for(int k=0; k<=grado; k++){
		suma=0.0;
		for(int i=0; i<nDatos; i++){
			suma+=potencia(x[i], k)*y[i];
		}
		t[k]=suma;
	}

	for(int i=0; i<=grado; i++){
		for(int j=0; j<=grado; j++){
			m[i][j]=s[i+j];
		}
	}
}

La función coeficientes llama a la función auxiliar potencia para calcular la potencia de un número elevado a un exponente entero

private double potencia(double base, int exp){
	double producto=1.0;
	for(int i=0; i<exp; i++){
		producto*=base;
	}
	return producto;
}

Resolución del sistema de ecuaciones

El sistema de ecuaciones se expresa en forma matricial

A X=B                    

donde A es la matriz de los coeficientes, B es la columna de términos constantes, y X la columna de las incógnitas. Si el determinante de A es no nulo, existe una matriz inversa A^-1. Multiplicando a la izquierda ambos miembros de la ecuación (1) por A^-1 obtenemos la columna X de las incógnitas, es decir, la solución del sistema.

${\displaystyle \begin{array}{l}{A}^{-1}AX=A^{-1}B\\ X=A^{-1}B\end{array}}$

El código de la función que calcula los coeficientes del polinomio aproximador es.

public void calculaPolinomio()  {
		 coeficientes();
        Vector ti=new Vector(t);
        Matriz mc = new Matriz (m);
        if (mc.determinante() == 0){
        	System.out.println("El sistema no tiene solucion única");
        }
        Vector solucion=Matriz.producto(Matriz.inversa(mc), ti);
        for(int i=0; i<=grado; i++){
	         a[i] = solucion.x[i];
	    }
  }

El código completo de la clase PolRegresion es el siguiente

public class PolRegresion {
  private double[] x;  //datos
  private double[] y;
  private int nDatos;
  double[][] m;    //matriz de los coeficientes
  double[] t;      //términos independientes
  public double[] a; //polinomio   a[0]+a[1]·x+a[2]·x2+...
  public int grado; //grado del polinomio

  public PolRegresion(double[] x, double[] y, int grado) {
    this.x=x;
    this.y=y;
    nDatos=x.length;
    this.grado=grado;
    t=new double[grado+1];
    m=new double[grado+1][grado+1];
    a=new double[grado+1];
  }

  private void coeficientes(){
    double[] s=new double[2*grado+1];
    double suma;
    for(int k=0; k<=2*grado; k++){
      suma=0.0;
      for(int i=0; i<nDatos; i++){
        suma+=potencia(x[i], k);
      }
      s[k]=suma;
    }
    for(int k=0; k<=grado; k++){
      suma=0.0;
      for(int i=0; i<nDatos; i++){
        suma+=potencia(x[i], k)*y[i];
      }
      t[k]=suma;
    }
    for(int i=0; i<=grado; i++){
      for(int j=0; j<=grado; j++){
        m[i][j]=s[i+j];
      }
    }
  }

  private double potencia(double base, int exp){
    double producto=1.0;
    for(int i=0; i<exp; i++){
      producto*=base;
    }
    return producto;
  }
 public void calculaPolinomio()  {
		    coeficientes();
        Vector ti=new Vector(t);
        Matriz mc = new Matriz (m);
        if (mc.determinante() == 0){
        	System.out.println("El sistema no tiene solucion única");
        }
        Vector solucion=Matriz.producto(Matriz.inversa(mc), ti);
        for(int i=0; i<=grado; i++){
	         a[i] = solucion.x[i];
	    }
  }
}

El procedimiento de Seidel

Finalmente, nos queda la tarea de resolver el sistema de n ecuaciones con n incógnitas (n es el grado del polinomio). El procedimiento empleando es el de Seidel. Explicaremos este procedimiento mediante un ejemplo. Sea el sistema lineal de tres ecuaciones

${\displaystyle \begin{array}{l}10x_0+x_1+x_2=12\\ 2x_0+10x_1+x_2=13\\ 2x_0+2x_1+10x_2=14\end{array}}$

Se despeja x₁ en la primera ecuación, x₂ en la segunda y x₃ en la tercera. Reduciéndose el sistema a una forma conveniente para aplicar el procedimiento de iteración o de aproximaciones sucesivas.

${\displaystyle \begin{array}{l}{x}_0=1.2+0.0+0.1x_1-0.1x_2\\ x_1=1.3-0.2x_0+0.0-0.1x_2\\ x_2=1.4-0.2x_0-{0.12}_1+0.0\end{array}}$        (4)

Como podemos apreciar, las diagonales de la matriz de los coeficientes de las x son ceros.

Tomemos como aproximación inicial

${\displaystyle x_0^0=\mathrm{1.2,}{x}_1^0=0.\text{0}\text{, }{x}_2^0=0.0}$

La primera aproximación se escribe

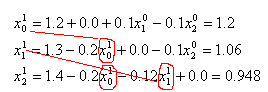
Se introduce la primera aproximación de x₀  en la segunda ecuación. Se introduce la primera aproximación de x₀ y de x₁ en la tercera ecuación, y así sucesivamente. De este modo el método de Seidel ofrece una mejor convergencia que la iteración simple.

La segunda aproximación es

${\displaystyle \begin{array}{l}{x}_0^2=1.2+0.0+0.1x_1^1-0.1x_2^1=0.9992\\ x_1^2=1.3-0.2x_0^2+0.0-0.1x_2^1=1.00536\\ x_2^2=1.4-0.2x_0^2-0.12x_1^2+0.0=0.999098\end{array}}$

En general el método se Seidel lo podemos escribir del siguiente modo.

${\displaystyle \begin{array}{l}{x}_0^{k+1}={\beta }_0+{\displaystyle \sum _{j=1}^n{\alpha }_{0j}{x}_j^k}\\ x_1^{k+1}={\beta }_1+{\alpha }_{10}{x}_0^{k+1}+{\displaystyle \sum _{j=2}^n{\alpha }_{1j}{x}_j^k}\\ x_i^{k+1}={\beta }_i+{\displaystyle \sum _{j=0}^{i-1}{\alpha }_{ij}{x}_j^{k+1}}+{\displaystyle \sum _{j=i+1}^n{\alpha }_{ij}{x}_j^k}\\ x_n^{k+1}={\beta }_n+{\displaystyle \sum _{j=0}^{n-1}{\alpha }_{ij}{x}_j^{k+1}}\end{array}}$

En todo proceso iterativo, es preciso establecer la condición de finalización, no puede correr el proceso de forma indefinida. El error relativo entre dos iteraciones consecutivos k y k+1 de los valores que toman cada una de las incógnitas x_i deberá ser menor que un cierto valor (por ejemplo, una milésima).

${\displaystyle \left|\frac{x_i^k-x_i^{k+1}}{x_i^k}\right|<0.001i=\mathrm{0...}n}$

Veamos ahora el código

En primer lugar, transformamos la matriz m de los coeficientes del sistema de ecuaciones (3) y el vector t de los términos independientes, para expresarlo de la forma (4) adecuada para la iteración. Para ello, se divide los elementos de cada fila i por el elemento correspondiente de la diagonal principal m[i][i] y se cambia de signo. Los elementos de la diagonal m[i][i] se hacen cero.

for(int i=0; i<=grado; i++){
	aux=m[i][i];
	for(int j=0; j<=grado; j++){
		m[i][j]=-m[i][j]/aux;
	}
	t[i]=t[i]/aux;
	m[i][i]=0.0;
}

Se elige la aproximación inicial, y se guardan en el array p de las incógnitas

p[0]=t[0];
for(int i=1; i<=grado; i++){
	p[i]=0.0;
}

Se calcula siguiente aproximación y se guarda en el array a de las incógnitas

for(int i=0; i<=grado; i++){
	a[i]=t[i];
	for(int j=0; j<i; j++){
		a[i]+=m[i][j]*a[j];
	}
	for(int j=i+1; j<=grado; j++){
		a[i]+=m[i][j]*p[j];
	}
}

La iteración actual a es la iteración anterior p en el siguiente cálculo

for(int i=0; i<=grado; i++){
	p[i]=a[i];
}

El proceso se repite, hasta que se cumple la condición de finalización.Para ello, calculamos el error relativo de cada una de las incógnitas. Guardamos en la variable maximo el mayor de los errores relativos.

maximo=0.0;
for(int i=0; i<=grado; i++){
	error=Math.abs((a[i]-p[i])/a[i]);
	if (error>maximo) maximo=error;
}

Todo el procedimiento lo ponemos en el interior de un bucle do...while que se ejecuta hasta que se cumple que el valor de la variable maximo sea menor o igual que una milésima.

double error=0.0, maximo=0.0;
do{
	error=0.0;
	maximo=0.0;
	for(int i=0; i<=grado; i++){
		a[i]=t[i];
		for(int j=0; j<i; j++){
			a[i]+=m[i][j]*a[j];
		}
		for(int j=i+1; j<=grado; j++){
			a[i]+=m[i][j]*p[j];
		}
		error=Math.abs((a[i]-p[i])/a[i]);
		if (error>maximo) maximo=error;
	}
	for(int i=0; i<=grado; i++){
		p[i]=a[i];
	}
}while(maximo>0.001);

El código alternativo de la función calculaPolinomio de la clase PolRegresion es el siguiente

public class PolRegresion {
  //...

//procedimiento de Seidel
  public void calculaPolinomio(){
    coeficientes();
//matriz
    double aux;
    for(int i=0; i<=grado; i++){
        aux=m[i][i];
      for(int j=0; j<=grado; j++){
        m[i][j]=-m[i][j]/aux;
      }
      t[i]=t[i]/aux;
      m[i][i]=0.0;
  }
// aproximación inicial
    double[] p=new double[grado+1];
    p[0]=t[0];
    for(int i=1; i<=grado; i++){
      p[i]=0.0;
    }
//aproximaciones  sucesivas
    double error=0.0, maximo=0.0;
    do{
      maximo=0.0;
      for(int i=0; i<=grado; i++){
        a[i]=t[i];
        for(int j=0; j<i; j++){
          a[i]+=m[i][j]*a[j];
        }
        for(int j=i+1; j<=grado; j++){
          a[i]+=m[i][j]*p[j];
        }
        error=Math.abs((a[i]-p[i])/a[i]);
        if (error>maximo)   maximo=error;
      }
      for(int i=0; i<=grado; i++){
          p[i]=a[i];
      }
    }while(maximo>0.001);

  }
}

Ejercicios

Determinar el polinomio aproximador de segundo grado para la siguientes tablas de datos, tomadas de una experiencia con fluidos

El siguiente applet permite introducir los datos experimentales y ajustarlos mediante un polinomio de grado menor o igual al número de datos. Los datos que aparecen cuando se inicia el applet en los controles de edición corresponden a la primera tabla.

Se elige el grado del polinomio pulsando en el botón titulado Grado polinomio>> y a continuación se pulsa en el botón titulado Calcular.

Se observa a la derecha la representación de los datos, del polinomio de ajuste y los valores de los coeficientes del polinomio.

P(x)=a₀+a₁x+a₂x²+...a_nxⁿ

Para ensayar con otros datos se pulsa el botón titulado Borrar, y a continuación se introducen los pares de datos en los controles de edición respectivos.

Referencias

B.P. Demidowitsch, Maron, Schuwalowa. Métodos numéricos de análisis. Editorial Paraninfo (1978), págs 21-23.

Demidovich, Maron. Cálculo numérico fundamental. Editorial Paraninfo (1977), págs 339-340.

Curso Interactivo de Física en Internet © Ángel Franco García