Modos normales de vibración de una barra elástica

Vamos a comprobar que los modos de vibración de una barra con ambos extremos fijos son similares a los de una cuerda aunque su descripción analítica es mucho más complicada.

En primer lugar, volvemos a obtener la fórmula de las frecuencias de los modos normales de vibración de una cuerda cuyos extremos están fijos por otro procedimiento más general que nos va a servir de modelo para describir los modos de vibración de una barra con ambos extremos fijos.

Ondas estacionarias en una cuerda

La ecuación diferencial del movimiento ondulatorio es

$v^{2} \frac{\partial^{2} ψ}{\partial x^{2}} = \frac{\partial^{2} ψ}{\partial t^{2}}$

siendo v la velocidad de propagación de las ondas en la cuerda y ψ el desplazamiento trasversal de un punto x de la cuerda en el instante t.

Estudiamos una solución de la forma

ψ(x,t)=y(x)·sin(ωt)

Cada punto de la cuerda vibra con una amplitud y(x) y con frecuencia angular ω.

La ecuación diferencial se convierte en

$\frac{d^{2} y}{d x^{2}} + \frac{ω^{2}}{v^{2}} y = 0$

La solución de esta ecuación diferencial, similar a la de un M.A.S., es

y=Asin (kx)+Bcos(kx) con k=ω/v que es el número de onda

Las condiciones de contorno son:

La cuerda está fija por sus extremos x=0 y x=L

De la primera condición, tenemos que B=0.

y de la segunda,

sin(kL)=0 o bien, kL=nπ, con n=1, 2, 3,…

que nos da los distintas frecuencias de vibración de la cuerda

$f_{n} = \frac{ω_{n}}{2 π} = v \frac{n}{2 L} n = 1, 2, 3, ...$

La amplitud de las oscilaciones de los puntos x de la cuerda en el modo normal n es

$y_{n} (x) = A \sin (\frac{n π}{L} x)$

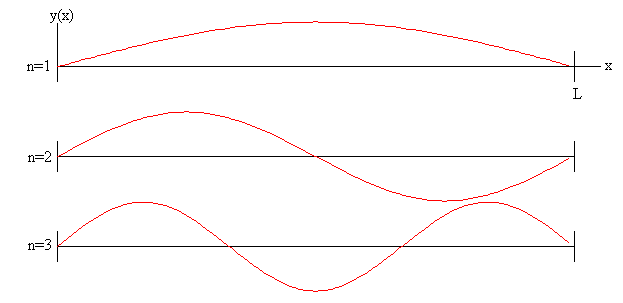
Estas funciones cumplen que

$\int_{0}^{L} y_{n}^{2} (x) \cdot d x = \frac{A^{2}}{2} \int_{0}^{L} (1 - cos (\frac{2 n π}{L} x)) d x = \frac{A^{2}}{2} {(x - \frac{L}{2 n π} \sin (\frac{2 n π}{L} x))}_{0}^{L} = \frac{A^{2}}{2} L$

La integral es el área bajo la curva de la figura inferior.

Modos normales de vibración de una barra elástica con extremos fijos

Para encontrar los modos normales de vibración de una barra elástica con ambos extremos fijos seguimos un procedimiento similar

La ecuación diferencial del movimiento de un elemento de la barra es

$\frac{\partial^{4} ψ}{\partial x^{4}} + \frac{ρ a b}{Y I} \frac{\partial^{2} ψ}{\partial t^{2}} = 0$

Siendo ψ el desplazamiento trasversal de un punto x de la barra en el instante t.

ρ es la densidad de la barra

Y es el módulo de Young del material de la barra.

I=ab³/12 es el momento de inercia de la sección trasversal rectangular de la barra de anchura a y espesor b.

Estudiamos una solución de la forma

ψ(x,t)=y(x)·sin(ωt)

Cada punto x de la barra vibra con una amplitud y(x) y con frecuencia angular ω.

La ecuación diferencial se convierte en

$\frac{d^{4} y}{d x^{4}} - \frac{ρ a b}{Y I} ω^{2} y = 0$

Las raíces de la ecuación característica son

$r^{4} - q^{4} = 0 q = {(\frac{ρ a b}{Y I} ω^{2})}^{1 / 4}$

son dos raíces reales y dos imaginarias

r=q, r=-q, r=iq, r=-iq

La solución general es

$y (x) = C_{1} e^{q x} + C_{2} e^{- q x} + C_{3} e^{i q x} + C_{4} e^{- i q x}$

o de forma equivalente

y=A₁sinh(qx)+A₂·cosh(qx)+A₃·sin(qx)+A₄·cos(qx)

La pendiente o derivada de y es,

$\frac{d y}{d x} = q (A_{1} \cosh (q x) + A_{2} \sinh (q x) + A_{3} \cos (q x) - A_{4} \sin (q x))$

Condiciones de contorno.

La barra está firmemente sujeta por sus extremo x=0, y la pendiente en este punto es dy/dx=0.

0=A₂+A₄0=A₁+A₃

La barra está firmemente sujeta por sus extremo x=L, y la pendiente en este punto es dy/dx=0.

0=A₁(sinh(qL)-sin(qL))+A₂(cosh(qL)-cos(qL))
0=A₁(cosh(qL)-cos (qL))+A₂(sinh(qL)+sin(qL))

Eliminado A₁ y A₂ obtenemos una ecuación trascendente en qL

(sinh(qL)-sin(qL))·(sinh(qL)+sin(qL))-(cosh(qL)-cos (qL))²=0

Las raíces r_n=q_n·L de esta ecuación se calculan por el procedimiento numérico del punto medio, sus primeros cinco valores son:

r_n=4.73, 7.85, 11.00, 14.14, 17.27

Conocido los valores posibles de q_n se calculan las frecuencias de vibración ω_n=2πf_n

$f_{n} = \frac{r_{n}^{2}}{2 π} \sqrt{\frac{Y I}{ρ a b L^{4}}} = C_{n} \sqrt{\frac{Y I}{ρ a b L^{4}}}$

Donde f_n es la frecuencia del modo normal n de vibración y C_n es un número que corresponde a este modo. Sus primeros valores son:

C₁=3.56, C₂=9.82, C₃=19.2, C₄=31.8, C₅=47.5, etc.

El coeficiente C_n es independiente de las características de la barra y el segundo término, bajo la raíz, depende del material y de las dimensiones de la barra.

La amplitud de la vibración y(x) de los distintos puntos x de la barra en el modo normal de vibración n es:

$y_{n} (x) = A {(sinh (q_{n} x) - sin (q_{n} x)) - \frac{sinh (q_{n} L) - sin (q_{n} L)}{cosh (q_{n} L) - cos (q_{n} L)} (cosh (q_{n} x) - cos (q_{n} x))}$

El valor de la constante de proporcionalidad A es la escala vertical. Para que todos los modos de vibración estén dibujados a la misma escala, se calcula A por procedimientos numéricos, de modo que

$\int_{0}^{L} y_{n}^{2} (x) d x = cte$

Aproximaciones

Cuando qL es grande exp(-qL)≈0 y el seno y el coseno hiperbólico se pueden aproximar a exp(-qL)/2.

Con esta aproximación la ecuación trascendente

(sinh(qL)-sin(qL))·(sinh(qL)+sin(qL))-(cosh(qL)-cos (qL))²=0

se reduce a

cos(qL)=1/exp(qL).

Si qL es grande cos(qL)=0, Las raíces de esta ecuación son

q_nL=π/2+nπ

Los cinco primeros valores de r_n=q_nL son

r_n=4.71, 7.85, 11.00, 14.14, 17.28.

Son prácticamente los mismos, que los calculados resolviendo la ecuación trascendente por procedimientos numéricos

La amplitud y(x) de los distintos puntos x de la barra en el modo normal de vibración n se puede aproximar a

$\begin{array}{l} y_{n} (x) \approx A {(sinh (q_{n} x) - sin (q_{n} x)) - (cosh (q_{n} x) - cos (q_{n} x))} \\ = A (- \exp (- q_{n} x) + cos (q_{n} x) - sin (q_{n} x)) \end{array}$

Se puede calcular el valor aproximado de la integral

$\begin{array}{l} \int_{0}^{L} y_{n}^{2} (x) d x = \int_{0}^{L} {1 - sin (2 q_{n} x) + \exp (- 2 q_{n} x) + 2 \exp (- q_{n} x) (sin (q_{n} x) -cos (q_{n} x))} d x = \\ {x + \frac{\cos (2 q_{n} x)}{2 q_{n}} - \frac{\exp (- 2 q_{n} x)}{2 q_{n}} - 2 \frac{\exp (- q_{n} x)}{q_{n}} sin (q_{n} x)}_{0}^{L} \approx L \end{array}$

Para obtener el integrando, hay que integrar dos veces por partes exp(-q_nx)·sin(q_nx), y lo mismo, exp(-q_nx)·cos (q_nx).

Para calcular el valor aproximado de la integral, se ha despreciado los términos exp(-q_nL) y exp(-2q_nL) y por otra parte, cos(2q_nL)=0.

Ejemplo:

Sea una barra de acero densidad ρ=7.8 g/cm³, módulo de Young Y=20.6·10¹⁰ N/m²

de dimensiones a=2.54 cm de ancho, b=0.76 mm de espesor y longitud L=20.3 cm.

El momento de inercia de la sección trasversal es

I=ab³/12=9.29·10^-13 m⁴

La frecuencia del modo fundamental de vibración vale

$f_{1} = 3.56 \sqrt{\frac{20.6 \cdot 10^{10} \cdot 9.29 \cdot 10^{- 13}}{7800 \cdot 0.0254 \cdot 0.00076 \cdot {0.203}^{4}}} = 3.56 \cdot 27.36 = 97 Hz$

La frecuencia del segundo modo normal de vibración será

f₂=9.82·27.36=269 Hz

y así, sucesivamente.

Como se describe en el artículo citado en las referencias, se puede diseñar una experiencia que permita excitar un modo normal de vibración de la barra, medir la frecuencia con un osciloscopio, y calcular el módulo de Young de la barra. Previamente, se miden las dimensiones de la barra (longitud, anchura y espesor) con los instrumentos adecuados y se pesa en una balanza para determinar su densidad (masa/volumen).

Actividades

El programa interactivo, resuelve la ecuación trascendente por el procedimiento del punto medio, calculando las cinco primeras raíces.

Representa la amplitud y(x) de los puntos x de la barra para los cinco primeros modos de vibración y proporciona el valor de los coeficientes C_n

Se pulsan los botones titulados Siguiente>> y <<Anterior