Modos normales de vibración de un sistema de muelles y partículas

En esta página, vamos a calcular los modos normales de vibración de un conjunto de partículas de la misma masa m unidas por muelles elásticos de constantes k, g, k, g, … tal como se muestra en la figura

Sistema formado por dos partículas

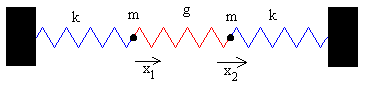
Ecuaciones del movimiento

$\begin{array}{l} m {\ddot{x}}_{1} = - k x_{1} + g (x_{2} - x_{1}) \\ m {\ddot{x}}_{2} = - g (x_{2} - x_{1}) - k x_{2} \end{array}$

Buscamos una solución de la forma

x₁=A₁cos(ωt), x₂=A₂cos(ωt)

En forma matricial, el sistema de ecuaciones se expresa

$(\begin{matrix} \frac{k + g}{m} & - \frac{g}{m} \\ - \frac{g}{m} & \frac{k + g}{m} \end{matrix}) (\begin{matrix} A_{1} \\ A_{2} \end{matrix}) = ω^{2} (\begin{matrix} A_{1} \\ A_{2} \end{matrix})$

Las frecuencias ω² son los valores propios de la matriz cuadrada, y los vectores propios las amplitudes de los modos normales de vibración

Valores propios ω²	Vectores propios
$\frac{k}{m}$	(A₁₁, A₁₁)
$\frac{k + 2 g}{m}$	(A₁₂, -A₁₂)

Los coeficientes A₁₁ y A₁₂ se determinan a partir de las condiciones iniciales: en el instante t=0, la posición de las partículas es x₁₀ y x₂₀.

Sistema formado por tres partículas

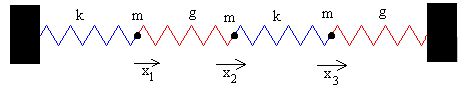
Ecuaciones del movimiento

$\begin{array}{l} m {\ddot{x}}_{1} = - k x_{1} + g (x_{2} - x_{1}) \\ m {\ddot{x}}_{2} = - g (x_{2} - x_{1}) + k (x_{3} - x_{2}) \\ m {\ddot{x}}_{3} = - k (x_{3} - x_{2}) - g x_{3} \end{array}$

Buscamos una solución de la forma

x₁=A₁cos(ωt), x₂=A₂cos(ωt), x₃=A₃cos(ωt)

En forma matricial, el sistema de ecuaciones se expresa

$(\begin{matrix} \frac{k + g}{m} & - \frac{g}{m} & 0 \\ - \frac{g}{m} & \frac{k + g}{m} & - \frac{k}{m} \\ 0 & - \frac{k}{m} & \frac{k + g}{m} \end{matrix}) (\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \end{matrix}) = ω^{2} (\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \end{matrix})$

Valores propios ω²	Vectores propios
$\frac{k + g - \sqrt{k^{2} + g^{2}}}{m}$	$(A_{11}, \frac{\sqrt{k^{2} + g^{2}}}{g} A_{11}, \frac{k}{g} A_{11})$
$\frac{k + g}{m}$	$(A_{12}, 0, - \frac{g}{k} A_{12})$
$\frac{k + g + \sqrt{k^{2} + g^{2}}}{m}$	$(A_{13}, - \frac{\sqrt{k^{2} + g^{2}}}{g} A_{13}, \frac{k}{g} A_{13})$

Los coeficientes A₁₁, A₁₂ y A₁₃ se determinan a partir de las condiciones iniciales: en el instante t=0, la posición de las partículas es x₁₀, x₂₀ y x₃₀

Sistema formado por N partículas

Calculamos los vectores y los valores propios de la matriz simétrica empleando el procedimiento de Jacobi

$(\begin{matrix} \frac{k + g}{m} & - \frac{g}{m} & 0 & ... & 0 & 0 & 0 & ... & 0 & 0 \\ - \frac{g}{m} & \frac{k + g}{m} & - \frac{k}{m} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - \frac{g}{m} & \frac{k + g}{m} & - \frac{k}{m} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - \frac{k}{m} & \frac{k + g}{m} \end{matrix})$

Actividades

Se ha fijado

La masa de las partículas, m=1 kg
La constante elástica de los muelles de color azul, k=1N/m

Se introduce

El número N de partículas, en el control de selección titulado Número de partículas
La constante elástica de los muelles de color rojo, g, en el control de edición titulado Constante

Se pulsa el botón titulado Nuevo

Observamos el primer modo normal de vibración, en la parte superior izquierda se proporciona la frecuencia angular ω₁.

Se pulsa el botón titulado Siguiente>>, observamos los siguientes modos normales ω₂, … etc.

Se pulsa el botón titulado Anterior<< para observar el modo normal de vibración anterior.

Las frecuencias de los modos de vibración se guardan en el control área de texto situado a la izquierda del applet.

Se pulsa el botón titulado Gráfica, para representar las frecuencias de los modos de vibración (en el eje vertical) en función de su orden.

Referencias

Lévesque L. Revisiting the coupled-mass system and analogy with a simple band gap structure. Eur. J. Phys. 27 (2006) pp. 133-145