Oscilaciones de una cadena diatómica lineal

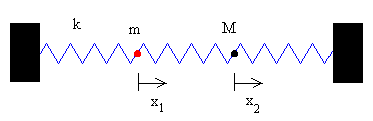
En esta página, vamos a calcular los modos normales de vibración de una cadena diatómica lineal formada por moléculas de masas m y M unidas por muelles elásticos de constante, k tal como se muestra en la figura

Sistema formado por dos partículas N=2

Ecuaciones del movimiento

$\begin{array}{l} m {\ddot{x}}_{1} = - k x_{1} + k (x_{2} - x_{1}) \\ M {\ddot{x}}_{2} = - k (x_{2} - x_{1}) - k x_{2} \end{array}$

Buscamos una solución de la forma

x₁=A₁cos(ωt), x₂=A₂cos(ωt)

El sistema de ecuaciones se expresa en forma matricial

$(\begin{matrix} \frac{2 k}{m} & - \frac{k}{m} \\ - \frac{k}{M} & \frac{2 k}{M} \end{matrix}) (\begin{matrix} A_{1} \\ A_{2} \end{matrix}) = ω^{2} (\begin{matrix} A_{1} \\ A_{2} \end{matrix})$

Como vemos la matriz ha dejado de ser simétrica

Las frecuencias son los valores propios de la matriz cuadrada |M- ω²I|=0, las raíces de la ecuación de segundo grado en ω² denominado polinomio característico

$\begin{array}{l} | \begin{matrix} \frac{2 k}{m} - ω^{2} & - \frac{k}{m} \\ - \frac{k}{M} & \frac{2 k}{M} - ω^{2} \end{matrix} | = 0 \\ ω^{4} - (\frac{2 k}{m} + \frac{2 k}{M}) ω^{2} + \frac{3 k^{2}}{m M} = 0 \end{array}$

La amplitudes para cada uno de los modos de vibración se calculan resolviendo el sistema de ecuaciones homogéneo

$(\frac{2 k}{m} - ω_{j}^{2}) A_{1 j} - \frac{k}{m} A_{2 j} = 0 j = 1,2$

Para el modo normal ω₁, se calcula A₂₁ en función de A₁₁
Para el modo normal ω₂, se calcula A₂₂ en función de A₁₂

El movimiento general de las partículas es una combinación lineal de los dos modos normales de vibración

x₁=A₁₁cos(ω₁t)+A₁₂cos(ω₂t)
x₂=A₂₁cos(ω₁t)+A₂₂cos(ω₂t)

Los coeficientes A₁₁ y A₁₂ se determinan a partir de las condiciones iniciales: en el instante t=0, la posición inicial de las partículas es x₁₀ y x₂₀

Sistema formado por tres partículas N=3

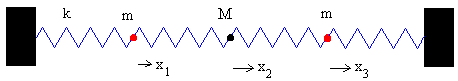
Ecuaciones del movimiento

$\begin{array}{l} m {\ddot{x}}_{1} = - k x_{1} + k (x_{2} - x_{1}) \\ M {\ddot{x}}_{2} = - k (x_{2} - x_{1}) + k (x_{3} - x_{2}) \\ m {\ddot{x}}_{3} = - k (x_{3} - x_{2}) - k x_{3} \end{array}$

Buscamos una solución de la forma

x₁=A₁cos(ωt), x₂=A₂cos(ωt), x₃=A₃cos(ωt)

El sistema de ecuaciones se expresa en forma matricial

$(\begin{matrix} \frac{2 k}{m} & - \frac{k}{m} & 0 \\ - \frac{k}{M} & \frac{2 k}{M} & - \frac{k}{M} \\ 0 & - \frac{k}{m} & \frac{2 k}{m} \end{matrix}) (\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \end{matrix}) = ω^{2} (\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \end{matrix})$

Como vemos la matriz ha dejado de ser simétrica

Las frecuencias son los valores propios de la matriz cuadrada, las raíces de la ecuación cúbica en ω²denominado polinomio característico

$\begin{array}{l} | \begin{matrix} \frac{2 k}{m} - ω^{2} & - \frac{k}{m} & 0 \\ - \frac{k}{M} & \frac{2 k}{M} - ω^{2} & - \frac{k}{M} \\ 0 & - \frac{k}{m} & \frac{2 k}{m} - ω^{2} \end{matrix} | = 0 \\ ω^{6} - (\frac{2 k}{M} + \frac{4 k}{m}) ω^{4} + (\frac{4 k^{2}}{m^{2}} + \frac{6 k^{2}}{m M}) ω^{2} - \frac{4 k^{3}}{m^{2} M} = 0 \end{array}$

La amplitudes para cada uno de los modos de vibración se calculan resolviendo el sistema de ecuaciones homogéneo

$\begin{array}{l} (\frac{2 k}{m} - ω_{j}^{2}) A_{1 j} - \frac{k}{m} A_{2 j} = 0 \\ - \frac{k}{M} A_{1 j} + (\frac{2 k}{M} - ω_{j}^{2}) A_{2 j} - \frac{k}{M} A_{3 j} = 0 \end{array}} j = 1,2,3$

Para el modo normal ω₁, se calcula A₂₁ y A₃₁ en función de A₁₁
Para el modo normal ω₂, se calcula A₂₂ y A₃₂ en función de A₁₂
Para el modo normal ω₃, se calcula A₂₃ y A₃₃ en función de A₁₃

El movimiento general de las partículas es una combinación lineal de los tres modos normales de vibración

x₁=A₁₁cos(ω₁t)+A₁₂cos(ω₂t)+A₁₃cos(ω₃t)
x₂=A₂₁cos(ω₁t)+A₂₂cos(ω₂t)+A₂₃cos(ω₃t)
x₃=A₃₁cos(ω₁t)+A₃₂cos(ω₂t)+A₃₃cos(ω₃t)

Los coeficientes A₁₁, A₁₂ y A₁₃ se determinan a partir de las condiciones iniciales: en el instante t=0, la posición inicial de las partículas es x₁₀, x₂₀yx₃₀

Sistema formado por N partículas

Para N partículas calculamos los valores y los vectores propios de la matriz

$(\begin{matrix} \frac{2 k}{m} & - \frac{k}{m} & 0 & ... & 0 & 0 & 0 & ... & 0 & 0 \\ - \frac{k}{M} & \frac{2 k}{M} & - \frac{k}{M} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - \frac{k}{m} & \frac{2 k}{m} & - \frac{k}{m} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - \frac{k}{m} & \frac{2 k}{m} \end{matrix})$

Como la matriz no es simétrica no podemos aplicar el procedimiento de Jacobi. Como alternativa, obtenemos los coeficientes del polinomio característico aplicando el procedimiento de Leverrier y calculamos las raíces del polinomio aplicando el procedimiento del punto medio para raíces múltiples.

Calculamos las amplitudes A_i mediante la relación de recurrencia

$- \frac{k}{m_{i}} A_{i - 1} + (\frac{2 k}{m_{i}} - ω_{j}^{2}) A_{i} - \frac{k}{m_{i}} A_{i + 1} = 0$

Donde m₁=m, m₂=M, m₃=m, m₄=M,…

Para el modo normal ω₁ se calculan las amplitudes A₂, A₃…. A_N en función de A₁, que denominaremos A₁₁, A₂₁, A₃₁… A_N1
Para el modo normal ω_j se calculan las amplitudes A₂, A₃…. A_N en función de A_1,que denominaremos A_1j, A_2j, A_3j… A_Nj
Para el modo normal ω_N se calculan las amplitudes A₂, A₃…. A_N en función de A_1,que denominaremos A_1N, A_2N, A_3N… A_NN.

Una vez calculadas las amplitudes A_ij para cada frecuencia ω_j se normalizan

$\sum_{i = 1}^{N} A_{i j}^{2} = 1 j = 1, 2, ... N$

Actividades

Se ha fijado

La masa, m=1 kg
La constante elástica de los muelles impares, k=1 N/m

Se introduce

El número N de partículas, en el control de selección titulado Número de partículas
La masa M de las otras partículas en el control de edición titulado Masa

Se pulsa el botón titulado Nuevo

Observamos el primer modo normal de vibración, en la parte superior izquierda se proporciona la frecuencia angular ω₁.

Se pulsa el botón titulado Siguiente>>, observamos los siguientes modos normales ω₂, … etc.

Se pulsa el botón titulado Anterior<< para observar el modo normal de vibración anterior.

Las frecuencias de los modos de vibración se guardan en el control área de texto situado a la izquierda del applet.

Se pulsa el botón titulado Gráfica, para representar las frecuencias de los modos de vibración (en el eje vertical) en función de su orden.

Relación de dispersión

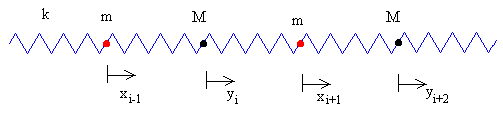
Consideremos una cadena lineal de moléculas diatómicas separados una distancia a en la situación de equilibrio, tal como se muestra en la figura.

Consideremos el movimiento de dos átomos contiguos.

El desplazamiento del átomo i de masa M denominamos y_i
El desplazamiento del átomo i+1 de masa m denominamos x_i₊₁

Ecuaciones del movimiento

$\begin{array}{l} M {\ddot{y}}_{i} = - k (y_{i} - x_{i - 1}) + k (x_{i + 1} - y_{i}) \\ m {\ddot{x}}_{i + 1} = - k (x_{i + 1} - y_{i}) + k (y_{i + 2} - x_{i + 1}) \end{array}$

Buscamos una solución de la forma

y_i=A_icos(ωt), con A_i=Asin(Kia)

x_i+1=A_i+1cos(ωt), con A_i+1=Bsin(K(i+1)a)

donde K se denomina número de onda

Introducimos estas soluciones en las dos ecuaciones diferenciales y obtenemos un sistema homogéneo de dos ecuaciones con dos incógnitas A y B.

A(-ω²M+2k)sin(Kia)-Bk(sin(K(i+1)a)+sin(K(i-1)a))=0
-Ak(sin(K(i+2)a)+sin(Kia))+B(-ω²m+2k) sin(K(i+1)a)=0

Teniendo en cuenta que

sin(K(i+1)a)+sin(K(i-1)a)=2sin(Kia)cos(Ka)
sin(K(i+2)a)+sin(Kia)= 2sin(K (i+1)a)cos(Ka)

y eliminamos A y B en el sistema homogéneo de dos ecuaciones

(-ω²M+2k) (-ω²m+2k)sen(Kia)sen(K(i+1)a)-4k²sen(Kia)cos²(Ka)sen(K(i+1)a))=0

Simplificando el factor común sin(Kia)sin(K(i+1)a)

$\begin{array}{l} ω^{4} - 2 k \frac{m + M}{m M} + 4 \frac{k^{2}}{m M} \sin^{2} (K a) = 0 \\ ω^{2} = k (\frac{1}{M} + \frac{1}{m}) \pm k \sqrt{({(\frac{1}{M} + \frac{1}{m})}^{2} - 4 \frac{\sin^{2} (K a)}{m M})} \end{array}$

Esta ecuación que relaciona la frecuencia ω con el número de onda K, se denomina relación de dispersión.

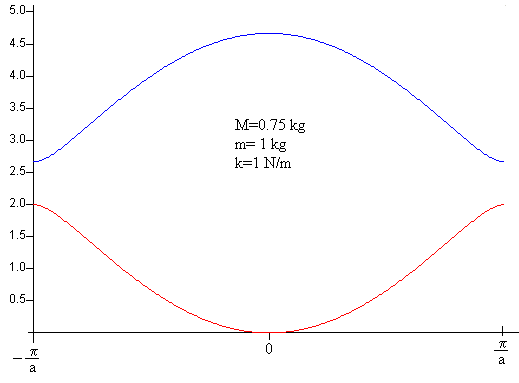
En la figura, se representa se representa la frecuencia angular ω en función del número de onda K en el intervalo (-π/a, +π/a). La curva superior (signo +) se denomina rama óptica, y la inferior (signo -) se denomina rama acústica.

Referencias

Runk R. B. Stul J. L. Anderson G. L. A laboratory analog for lattice dynamics. Am. J. Phys. (31) 1963, pp. 915-921