Oscilaciones de tres partículas unidas por muelles elásticos

En la página titulada “Dos osciladores acoplados” estudiamos las oscilaciones de dos partículas idénticas unidas a dos muelles de constante k y acopladas por un muelle de constante k_c.

En esta página, vamos a estudiar un sistema formado por tres partículas de la misma masa m unidas por muelles elásticos iguales de constante k, tal como se muestra en la figura.

Ecuaciones del movimiento de las partículas

Supongamos que la primera partícula se desplaza x₁ de la posición de equilibrio, que la segunda se desplaza x₂ y la tercera, se desplaza x_3.

En las figuras, se muestra las fuerzas sobre cada una de las partículas

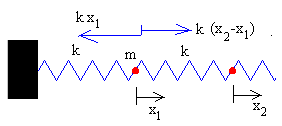	Ecuación del movimiento de la primera partícula $m {\ddot{x}}_{1} = - k x_{1} + k (x_{2} - x_{1})$
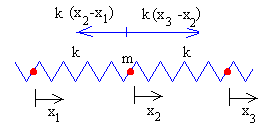	Ecuación del movimiento de la segunda partícula $m {\ddot{x}}_{2} = - k (x_{2} - x_{1}) + k (x_{3} - x_{2})$
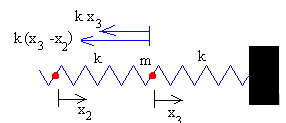	Ecuación del movimiento de la tercera partícula $m {\ddot{x}}_{3} = - k (x_{3} - x_{2}) - k x_{3}$

El símbolo, derivada segunda respecto del tiempo se escribe ahora

$\frac{d^{2} x}{d t^{2}} \equiv \ddot{x}$

Buscamos una solución de la forma

x_i=A_icos(ωt), i=1, 2, 3

que representa un MAS de amplitud A_i y frecuencia angular ω. Al ser la fase inicial π/2, la partícula parte del reposo en el instante t=0, de la posición x_0i

Teniendo en cuenta que la derivada segunda de x_i respecto del tiempo t es

${\ddot{x}}_{i} = - ω^{2} A_{i} \cos (ω t)$

Obtenemos el siguiente sistema de ecuaciones homogéneo

$\begin{array}{l} (\frac{2 k}{m} - ω^{2}) A_{1} - \frac{k}{m} A_{2} = 0 \\ - \frac{k}{m} A_{1} + (\frac{2 k}{m} - ω^{2}) A_{2} - \frac{k}{m} A_{3} = 0 \\ - \frac{k}{m} A_{2} + (\frac{2 k}{m} - ω^{2}) A_{3} = 0 \end{array}$

El determinante

$| \begin{matrix} \frac{2 k}{m} - ω^{2} & - \frac{k}{m} & 0 \\ - \frac{k}{m} & \frac{2 k}{m} - ω^{2} & - \frac{k}{m} \\ 0 & - \frac{k}{m} & \frac{2 k}{m} - ω^{2} \end{matrix} | = 0$

Las tres raíces de la ecuación cúbica en ω² son

$\begin{array}{l} ω_{1}^{2} = \frac{2 k}{m} (1 - \frac{\sqrt{2}}{2}) \\ ω_{2}^{2} = \frac{2 k}{m} \\ ω_{3}^{2} = \frac{2 k}{m} (1 + \frac{\sqrt{2}}{2}) \end{array}$

Para cada una de las frecuencias calculamos los coeficientes A₁, A₂ y A₃, que son las amplitudes de los modos normales de vibración.

Para la primera frecuencia ω₁.

$\begin{array}{l} (\frac{2 k}{m} - ω_{1}^{2}) A_{1} - \frac{k}{m} A_{2} = 0 A_{2} = A_{1} \sqrt{2} \\ - \frac{k}{m} A_{1} + (\frac{2 k}{m} - ω_{1}^{2}) A_{2} - \frac{k}{m} A_{3} = 0 A_{3} = A_{1} \end{array}$

La tercera ecuación

$- \frac{k}{m} A_{2} + (\frac{2 k}{m} - ω_{1}^{2}) A_{3} = 0$

nos permite verificar que los valores hallados de A₂ y A₃ son correctos

Una vez que conocemos el procedimiento para calcular las amplitudes A_idel primer modo normal de vibración calculamos los coeficientes para el segundo modo ω₂, que denominaremos B_i, y para el tercer modo ω₃, que denominaremos C_i. Los resultados son:

Segundo modo de vibración ω₂

B₂=0, B₃=-B₁

Tercer modo de vibración ω₃

$C_{2} = - C_{1} \sqrt{2} C_{3} = C_{1}$

El movimiento de cada partícula es una superposición de los tres modos de vibración

$\begin{array}{l} x_{1} = A_{1} \cos (ω_{1} t + ϕ_{1}) + B_{1} \cos (ω_{2} t + ϕ_{2}) + C_{1} \cos (ω_{3} t + ϕ_{3}) \\ x_{2} = A_{2} \cos (ω_{1} t + ϕ_{1}) + B_{2} \cos (ω_{2} t + ϕ_{2}) + C_{2} \cos (ω_{3} t + ϕ_{3}) \\ x_{3} = A_{3} \cos (ω_{1} t + ϕ_{1}) + B_{3} \cos (ω_{2} t + ϕ_{2}) + C_{3} \cos (ω_{3} t + ϕ_{3}) \end{array}$

Las velocidades de las partículas son :

$\begin{array}{l} \frac{d x_{1}}{d t} = - A_{1} ω_{1} \sin (ω_{1} t + ϕ_{1}) - B_{1} ω_{2} \sin (ω_{2} t + ϕ_{2}) - C_{1} ω_{3} \sin (ω_{3} t + ϕ_{3}) \\ \frac{d x_{2}}{d t} = - A_{2} ω_{1} \sin (ω_{1} t + ϕ_{1}) - B_{2} ω_{2} \sin (ω_{2} t + ϕ_{2}) - C_{2} ω_{3} \sin (ω_{3} t + ϕ_{3}) \\ \frac{d x_{3}}{d t} = - A_{3} ω_{1} \sin (ω_{1} t + ϕ_{1}) - B_{3} ω_{2} \sin (ω_{2} t + ϕ_{2}) - C_{3} ω_{3} \sin (ω_{3} t + ϕ_{3}) \end{array}$

Si las velocidades iniciales de las partículas son cero, las fases iniciales φ₁=φ₂=φ₃=0

$\begin{array}{l} x_{1} = A_{1} \cos (ω_{1} t) + B_{1} \cos (ω_{2} t) + C_{1} \cos (ω_{3} t) \\ x_{2} = A_{1} \sqrt{2} \cos (ω_{1} t) - C_{1} \sqrt{2} \cos (ω_{3} t) \\ x_{3} = A_{1} \cos (ω_{1} t) - B_{1} \cos (ω_{2} t) + C_{1} \cos (ω_{3} t) \end{array}$

Los valores de A₁, B₁ y C₁ se determinan a partir de las condiciones iniciales. En el instante t=0, las partículas parten del reposo desde las posiciones x₀₁, x₀₂, y x₀₃ respectivamente

$\begin{array}{l} x_{01} = A_{1} + B_{1} + C_{1} \\ x_{02} = A_{1} \sqrt{2} - C_{1} \sqrt{2} \\ x_{03} = A_{1} - B_{1} + C_{1} \end{array}$

Resolviendo el sistema de ecuaciones

$A_{1} = \frac{x_{01} + x_{03} + \sqrt{2} x_{02}}{4} B_{1} = \frac{x_{01} - x_{03}}{2} C_{1} = \frac{x_{01} + x_{03} - \sqrt{2} x_{02}}{4}$

Modos normales de vibración

El primer modo normal de vibración ω₁ se establece cuando A₁≠0, B₁=0 y C₁=0

$x_{03} = x_{01} x_{02} = \sqrt{2} x_{01}$

Las ecuaciones del movimiento de cada una de las partículas en este modo de vibración son

$\begin{array}{l} x_{1} = x_{01} \cos (ω_{1} t) \\ x_{2} = \sqrt{2} x_{01} \cos (ω_{1} t) \\ x_{3} = x_{01} \cos (ω_{1} t) \end{array}$

El segundo modo normal de vibración ω₂ se establece cuando A₁=0, B₁≠0 y C₁=0

$x_{03} = - x_{01} x_{02} = 0$

Las ecuaciones del movimiento de cada una de las partículas en este modo de vibración son

$\begin{array}{l} x_{1} = x_{01} \cos (ω_{2} t) \\ x_{2} = 0 \\ x_{3} = - x_{01} \cos (ω_{2} t) \end{array}$

El tercer modo normal de vibración ω₃ se establece cuando A₁=0, B₁=0 y C₁≠0

$x_{03} = x_{01} x_{02} = - \sqrt{2} x_{01}$

Las ecuaciones del movimiento de cada una de las partículas en este modo de vibración son

$\begin{array}{l} x_{1} = x_{01} \cos (ω_{3} t) \\ x_{2} = - \sqrt{2} x_{01} \cos (ω_{3} t) \\ x_{3} = x_{01} \cos (ω_{3} t) \end{array}$

Actividades

La masa de las partículas se ha fijado en m=1 kg
La constante de los muelles se ha fijado en k=1 N/m

Se introduce

La posición inicial x₀₁ de la primera partícula, actuando en la barra de desplazamiento titulada Posición X01.
La posición inicial x₀₂ de la segunda partícula, actuando en la barra de desplazamiento titulada Posición X02.
La posición inicial x₀₃ de la tercera partícula, actuando en la barra de desplazamiento titulada Posición X03.

Se pulsa el botón titulado Empieza

Si activamos la casilla titulada Gráfica y luego, pulsamos el botón titulado Empieza, se representa las posiciones x₁, x₂, y x₃ de cada una de las partículas en función del tiempo t.

Referencias

Lévesque L. Revisiting the coupled-mass system and analogy with a simple band gap structure. Eur. J. Phys. 27 (2006) pp. 133-145