Oscilaciones de una cadena monoatómica lineal

Vamos a estudiar los modos normales de vibración de un sistema formado por muelles y partículas, como continuación y generalización del sistema formado por tres osciladores acoplados. Este ejemplo nos ayudará a comprender los modos normales de vibración de una cuerda fija por sus extremos, también denominados ondas estacionarias.

Supongamos un conjunto de partículas de masas m₁, m₂, m3…m_N-1, m_N unidas por muelles elásticos de constantes k₀, k₁, k₂, k₃, … k_N-1, k_N.

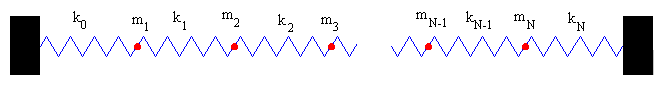
Ecuaciones del movimiento

En las figuras se muestran las fuerzas sobre la primera partícula de masa m₁, la partícula i y la última partícula N de masa m_N

	$m_{1} {\ddot{x}}_{1} = - k_{0} x_{1} + k_{1} (x_{2} - x_{1})$
	$m_{i} {\ddot{x}}_{i} = - k_{i - 1} (x_{i} - x_{i - 1}) + k_{i} (x_{i + 1} - x_{i})$
	$m_{N} {\ddot{x}}_{N} = - k_{N - 1} (x_{N} - x_{N - 1}) - k_{N} x_{N}$

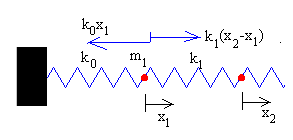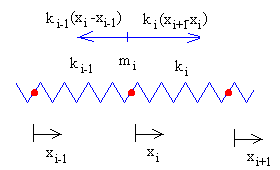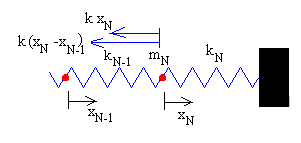El símbolo, derivada segunda respecto del tiempo se escribe ahora

$\frac{d^{2} x}{d t^{2}} \equiv \ddot{x}$

Resumiendo, las ecuaciones del movimiento de las partículas son

$\begin{array}{l} m_{1} {\ddot{x}}_{1} = - k_{0} x_{1} + k_{1} (x_{2} - x_{1}) \\ m_{2} {\ddot{x}}_{2} = - k_{1} (x_{2} - x_{1}) + k_{2} (x_{3} - x_{2}) \\ m_{3} {\ddot{x}}_{3} = - k_{2} (x_{3} - x_{2}) + k_{3} (x_{4} - x_{3}) \\ m_{i} {\ddot{x}}_{i} = - k_{i - 1} (x_{i} - x_{i - 1}) + k_{i} (x_{i + 1} - x_{i}) \\ m_{N - 1} {\ddot{x}}_{N - 1} = - k_{N - 2} (x_{N - 1} - x_{N - 2}) + k_{N - 1} (x_{N} - x_{N - 1}) \\ m_{N} {\ddot{x}}_{N} = - k_{N - 1} (x_{N} - x_{N - 1}) - k_{N} x_{N} \end{array}$

Buscamos una solución de la forma

x_i=A_icos(ωt)

Al ser la fase inicial π/2, las partículas parten del reposo en el instante t=0, de la posición x_0i

Teniendo en cuenta que la derivada segunda de x_i respecto del tiempo t es

${\ddot{x}}_{i} = - ω^{2} A_{i} \cos (ω t)$

Obtenemos el siguiente sistema de ecuaciones homogéneo

$\begin{array}{l} (\frac{k_{0} + k_{1}}{m_{1}} - ω^{2}) A_{1} - \frac{k_{1}}{m_{1}} A_{2} = 0 \\ - \frac{k_{1}}{m_{2}} A_{1} + (\frac{k_{1} + k_{2}}{m_{2}} - ω^{2}) A_{2} - \frac{k_{2}}{m_{2}} A_{3} = 0 \\ - \frac{k_{i - 1}}{m_{i}} A_{i - 1} + (\frac{k_{i - 1} + k_{i}}{m_{i}} - ω^{2}) A_{i} - \frac{k_{i}}{m_{i}} A_{i + 1} = 0 \\ - \frac{k_{N - 1}}{m_{N}} A_{N - 1} + (\frac{k_{N - 1} + k_{N}}{m_{N}} - ω^{2}) A_{N} = 0 \end{array}$

Que podemos expresar en forma matricial de la forma

$(\begin{matrix} \frac{k_{0} + k_{1}}{m_{1}} & - \frac{k_{1}}{m_{1}} & 0 & ... & 0 & 0 & 0 & ... & 0 & 0 \\ - \frac{k_{1}}{m_{2}} & \frac{k_{1} + k_{2}}{m_{2}} & - \frac{k_{2}}{m_{2}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - \frac{k_{i - 1}}{m_{i}} & \frac{k_{i - 1} + k_{i}}{m_{i}} & - \frac{k_{i}}{m_{i}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - \frac{k_{N - 1}}{m_{N}} & \frac{k_{N - 1} + k_{N}}{m_{N}} \end{matrix}) (\begin{matrix} A_{1} \\ A_{2} \\ A_{i} \\ A_{N} \end{matrix}) = ω^{2} (\begin{matrix} A_{1} \\ A_{2} \\ A_{i} \\ A_{N} \end{matrix})$

De forma simbólica podemos expresar M·X= ω²X, donde X es el vector columna de los coeficientes A₁, A₂... A_N.

Las frecuencias de los modos normales de vibración se calculan haciendo que el determinante de la matriz |M- ω²I|=0, donde I es la matriz unidad. Las raíces del polinomio de grado N en ω² son los valores propios de la matriz M. Los vectores propios son los valores de los coeficientes A_i para cada una de dichas frecuencias.

También, podemos calcular las amplitudes A_i de los modos normales de vibración para cada una de las frecuencias ω_j, empleando la relación de recurrencia

$- \frac{k_{i - 1}}{m_{i}} A_{i - 1} + (\frac{k_{i - 1} + k_{i}}{m_{i}} - ω_{j}^{2}) A_{i} - \frac{k_{i}}{m_{i}} A_{i + 1} = 0$

Para el modo normal de frecuencia ω₁ se calculan las amplitudes A₂, A₃…. A_N en función de A₁, que denominaremos A₁₁, A₂₁, A₃₁… A_N1, que son a su vez, las componentes del vector propio correspondiente al valor propio ω²₁
Para el modo normal de frecuencia ω_j se calculan las amplitudes A₂, A₃…. A_N en función de A₁que denominaremos A_1j, A_2j, A_3j… A_Nj, que son a su vez, las componentes del vector propio correspondiente al valor propio ω²_j
Para el modo normal de frecuencia ω_N se calculan las amplitudes A₂, A₃…. A_N en función de A₁que denominaremos A_N1, A_N2, A_N3… A_NN., que son a su vez, las componentes del vector propio correspondiente al valor propio ω²_N

Movimiento de las partículas

El movimiento de cada partícula es una superposición de todos los modos de vibración

x₁=A₁₁cos(ω₁·t+φ₁)+A₁₂cos(ω₂·t+φ₂)+...A_1N·cos(ω_N·t+φ_N)
x₂=A₂₁cos(ω₁·t+φ₁)+A₂₂cos(ω₂·t+φ₂)+....A_2N·cos(ω_N·t+φ_N)
...........
x_N=A_N1cos(ω₁·t+φ₁)+A_N2cos(ω₂·t+φ₂)+....A_NN·cos(ω_N·t+φ_N)

Se determinan los coeficientes A₁₁,A₁₂.... A_1N y las fases φ₁, φ₂...φ_N a partir de las condiciones iniciales: en el instante t=0, las posiciones de las partículas son x₁₀, x₂₀, x₃₀,...x_N0.y sus velocidades iniciales son (dx₁/dt)₀, (dx₂/dt)₀.... (dx_N/dt)₀.

Si las partículas parten del reposo, las fases iniciales son cero, φ₁=φ₂=...φ_N =0

Modos normales de vibración

El primer modo normal de vibración de frecuencia ω₁ se establece cuando A₁₂=A₁₃=…A_1N=0 y A₁₁≠0

El movimiento de las partículas es

x₁=A₁₁cos(ω₁·t)
x₂=A₂₁cos(ω₁·t)
...........
x_N=A_N1cos(ω₁·t)

Donde A₁₁, A₂₁, ...A_N1 son las componentes del vector propio correspondientes correspondiente al valor propio ω²₁

El modo normal de vibración de frecuencia ω_j se establece cuando A₁₁=A₁₃=…A_1N=0 y A_1j≠0

El movimiento de las partículas es

x₁=A_1jcos(ω_j·t)
x₂=A_2jcos(ω_j·t)
...........
x_N=A_Njcos(ω_j·t)

Donde A_1j, A_2j, ...A_Nj son las componentes del vector propio correspondientes correspondiente al valor propio ω²_j

Hasta aquí hemos formulado el problema general, pasamos a hora a resolver diversos casos particulares

Casos particulares

Un caso particular importante, es una cadena monoatómica lineal cuando las constantes de los muelles elásticos tienen el mismo valor k₀=k₁=k₂=k₃, …=k_N-1=k_N=k, y las partículas tienen la misma masa m₀=m₁=m₂=m₃, …=m_N-1=m_N=m

Calculamos los valores propios ω² y los vectores propios de la matriz simétrica M por el procedimiento de Jacobi.

$(\begin{matrix} \frac{2 k}{m} & - \frac{k}{m} & 0 & ... & 0 & 0 & 0 & ... & 0 & 0 \\ - \frac{k}{m} & \frac{2 k}{m} & - \frac{k}{m} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & - \frac{k}{m} & \frac{2 k}{m} & - \frac{k}{m} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - \frac{k}{m} & \frac{2 k}{m} \end{matrix})$

Ejemplos:

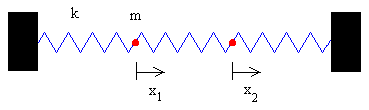
Sistema formado por dos partículas N=2

Ecuaciones del movimiento

$\begin{array}{l} m {\ddot{x}}_{1} = - k x_{1} + k (x_{2} - x_{1}) \\ m {\ddot{x}}_{2} = - k (x_{2} - x_{1}) - k x_{2} \end{array}$

Buscamos una solución de la forma

x₁=A₁cos(ωt), x₂=A₂cos(ωt)

En forma matricial, el sistema de ecuaciones se expresa

$(\begin{matrix} \frac{2 k}{m} & - \frac{k}{m} \\ - \frac{k}{m} & \frac{2 k}{m} \end{matrix}) (\begin{matrix} A_{1} \\ A_{2} \end{matrix}) = ω^{2} (\begin{matrix} A_{1} \\ A_{2} \end{matrix})$

Las frecuencias ω² son los valores propios de la matriz cuadrada y los vectores propios, las amplitudes de los modos normales de vibración

Valores propios ω² Vectores propios

$\frac{k}{m}$ (A₁₁, A₁₁)

$3 \frac{k}{m}$ (A₁₂, -A₁₂)

Los coeficientes A₁₁ y A₁₂ se determinan a partir de las condiciones iniciales

Sistema formado por tres partículas N=3

Las ecuaciones del movimiento son:

$\begin{array}{l} m {\ddot{x}}_{1} = - k x_{1} + k (x_{2} - x_{1}) \\ m {\ddot{x}}_{2} = - k (x_{2} - x_{1}) + k (x_{3} - x_{2}) \\ m {\ddot{x}}_{3} = - k (x_{3} - x_{2}) - k x_{3} \end{array}$

Buscamos una solución de la forma

x₁=A₁cos(ωt), x₂=A₂cos(ωt), x₃=A₃cos(ωt)

En forma matricial, el sistema de ecuaciones se expresa

$(\begin{matrix} \frac{2 k}{m} & - \frac{k}{m} & 0 \\ - \frac{k}{m} & \frac{2 k}{m} & - \frac{k}{m} \\ 0 & - \frac{k}{m} & \frac{2 k}{m} \end{matrix}) (\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \end{matrix}) = ω^{2} (\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \end{matrix})$

Las frecuencias ω² son los valores propios de la matriz cuadrada y los vectores propios, las amplitudes de los modos normales de vibración

Valores propios ω² Vectores propios

$\frac{2 k}{m} (1 - \frac{\sqrt{2}}{2})$ $(A_{11}, A_{11} \sqrt{2}, A_{11})$

$\frac{2 k}{m}$ (A₁₂, 0, -A₁₂)

$\frac{2 k}{m} (1 + \frac{\sqrt{2}}{2})$ $(A_{13}, - A_{13} \sqrt{2}, A_{13})$

Los coeficientes A₁₁, A₁₂ y A₁₃ se determinan a partir de las condiciones iniciales

Sistema formado por cuatro partículas N=4

$\begin{array}{l} m {\ddot{x}}_{1} = - k x_{1} + k (x_{2} - x_{1}) \\ m {\ddot{x}}_{2} = - k (x_{2} - x_{1}) + k (x_{3} - x_{2}) \\ m {\ddot{x}}_{3} = - k (x_{3} - x_{2}) + k (x_{4} - x_{3}) \\ m {\ddot{x}}_{4} = - k (x_{4} - x_{3}) - k x_{4} \end{array}$

Buscamos una solución de la forma

x₁=A₁cos(ωt), x₂=A₂cos(ωt), x₃=A₃cos(ωt), x₄=A₄cos(ωt)

En forma matricial, el sistema de ecuaciones se expresa

$(\begin{matrix} \frac{2 k}{m} & - \frac{k}{m} & 0 & 0 \\ - \frac{k}{m} & \frac{2 k}{m} & - \frac{k}{m} & 0 \\ 0 & - \frac{k}{m} & \frac{2 k}{m} & - \frac{k}{m} \\ 0 & 0 & - \frac{k}{m} & \frac{2 k}{m} \end{matrix}) (\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \\ A_{4} \end{matrix}) = ω^{2} (\begin{matrix} A_{1} \\ A_{2} \\ A_{3} \\ A_{4} \end{matrix})$

Las frecuencias ω² son los valores propios de la matriz cuadrada y los vectores propios, las amplitudes de los modos normales de vibración

Valores propios ω² Vectores propios

$\frac{k}{m} (2 - \sqrt{\frac{3 + \sqrt{5}}{2}}) = \frac{k}{m} (2 - \frac{\sqrt{5} + 1}{2})$ $(A_{11}, \frac{\sqrt{5} + 1}{2} A_{11}, \frac{\sqrt{5} + 1}{2} A_{11}, A_{11})$

$\frac{k}{m} (2 - \frac{\sqrt{5} - 1}{2})$ $(A_{12}, \frac{\sqrt{5} - 1}{2} A_{12}, - \frac{\sqrt{5} - 1}{2} A_{12}, - A_{12})$

$\frac{k}{m} (2 + \frac{\sqrt{5} - 1}{2})$ $(A_{13}, - \frac{\sqrt{5} - 1}{2} A_{13}, - \frac{\sqrt{5} - 1}{2} A_{13}, A_{13})$

$\frac{k}{m} (2 + \frac{\sqrt{5} + 1}{2})$ $(A_{14}, - \frac{\sqrt{5} + 1}{2} A_{14}, \frac{\sqrt{5} + 1}{2} A_{14}, - A_{14})$

Los coeficientes A₁₁, A₁₂, A₁₃ y A₁₄ se determinan a partir de las condiciones iniciales

El lector pude comprobar con la calculadora que las frecuencias de los modos normales de vibración para un sistema formado por N partículas de masa m unidas a muelles elásticos de constante k, se pueden obtenerse mediante la fórmula

$4 \frac{k}{m} \sin^{2} (\frac{n π}{2 N + 2}) 1 \leq n \leq N$

Para su justificación consúltese el artículo citado en las referencias

Actividades

Se ha fijado

La masa de las partículas, m=1 kg
La constante elástica de los muelles, k=1N/m

Se introduce

El número N de partículas, en el control de selección titulado Número de partículas

Se pulsa el botón titulado Nuevo

Observamos el primer modo normal de vibración, en la parte superior izquierda se proporciona la frecuencia angular ω₁.

Se pulsa el botón titulado Siguiente>>, observamos los siguientes modos normales ω₂, … etc.

Se pulsa el botón titulado Anterior<< para observar el modo normal de vibración anterior.

Relación de dispersión

Como vemos en la figura tenemos N partículas de masa m unidas a N+1 muelles iguales de constante k, cuyos extremos están fijos. La separación de equilibrio entre las partículas es a.

Supongamos que en un instante dado t, la partícula 1 se desplaza x₁, la partícula 2 se desplaza x₂, ... la partícula i se desplaza x_i, etc.

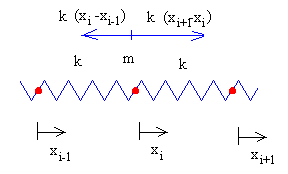La ecuación del movimiento para la partícula i será entonces

$m \frac{d^{2} x_{i}}{d t^{2}} = - k (x_{i} - x_{i - 1}) + k (x_{i + 1} - x_{i})$

Supongamos, que el sistema vibra en un modo de frecuencia ω. Cada partícula describirá un M.A.S. de la misma frecuencia ω , pero cuya amplitud A_i vamos a calcular.

x_i=A_i·cos(ω t)

Introduciendo esta expresión en la ecuación diferencial que describe el movimiento de cada partícula, obtenemos, la relación de recurrencia.

$\begin{array}{l} A_{i + 1} + A_{i - 1} = A_{i} (2 - \frac{m}{k} ω^{2}) \\ A_{i + 1} + A_{i - 1} = A_{i} s A_{0} = 0 A_{N + 1} = 0 \end{array}$

Ejemplos:

Sistema formado por dos partículas, N=2

$\begin{array}{l} N = 2 {\begin{cases} A_{2} = A_{1} s \\ A_{1} = A_{2} s \end{cases} \\ | \begin{matrix} 1 & - s \\ s & - 1 \end{matrix} | = 0 s^{2} - 1 = 0 {\begin{cases} s = 1 \\ s = - 1 \end{cases} \end{array}$

Conocido s despejamos ω² y obtenemos las frecuencias de los modos normales para N=2

Sistema formado por tres partículas, N=3

$\begin{array}{l} N = 3 {\begin{cases} A_{2} = A_{1} s \\ A_{3} + A_{1} = A_{2} s \\ A_{2} = A_{3} s \end{cases} \\ | \begin{matrix} 0 & 1 & - s \\ 1 & - s & 1 \\ s & - 1 & 0 \end{matrix} | = 0 2 s - s^{3} = 0 {\begin{cases} s = 0 \\ s = \sqrt{2} \\ s = - \sqrt{2} \end{cases} \end{array}$

Conocido s despejamos ω² y obtenemos las frecuencias de los modos normales para N=3

Sistema formado por cuatro partículas, N=4

$\begin{array}{l} N = 4 {\begin{cases} A_{2} = A_{1} s \\ A_{3} + A_{1} = A_{2} s \\ A_{4} + A_{2} = A_{3} s \\ A_{3} = A_{4} s \end{cases} \\ | \begin{matrix} 0 & 0 & 1 & - s \\ 0 & 1 & - s & 1 \\ 1 & - s & 1 & 0 \\ s & - 1 & 0 & 0 \end{matrix} | = 0 s^{4} - 3 s^{2} + 1 = 0 {\begin{cases} s = \sqrt{\frac{3 + \sqrt{5}}{2}} = \frac{\sqrt{5} + 1}{2} \\ s = - \sqrt{\frac{3 + \sqrt{5}}{2}} = - \frac{\sqrt{5} + 1}{2} \\ s = \sqrt{\frac{3 - \sqrt{5}}{2}} = \frac{\sqrt{5} - 1}{2} \\ s = - \sqrt{\frac{3 + \sqrt{5}}{2}} = - \frac{\sqrt{5} - 1}{2} \end{cases} \end{array}$

Conocido s despejamos ω² y obtenemos las frecuencias de los modos normales para N=4

Para N→∞, buscamos una solución a esta ecuación de la forma

A_i=A·sin(K·ia)

donde K es el número de onda K=2π/λ. La realción de recurrencia se escribe

Asin(Kia+Ka)+ Asin(Kia-Ka)= Asin(Kia)(2-mω²/k)

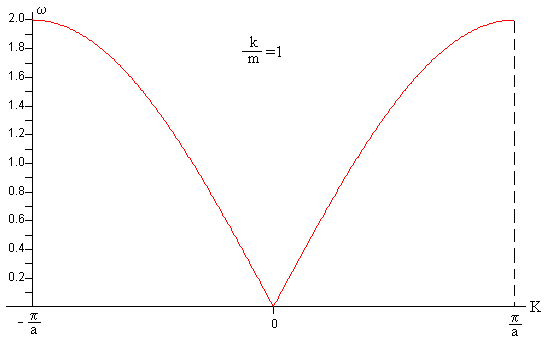
$\begin{array}{l} 2 \cos (K a) = (2 - \frac{m}{k} ω^{2}) \\ ω = 2 \sqrt{\frac{k}{m}} \sin (\frac{K a}{2}) \end{array}$

Esta ecuación que relaciona la frecuencia angular ω con el número de onda K, se denomina relación de dispersión.

En la figura, se representa la frecuencia angular ω en función del número de onda K en el intervalo (-π/a, +π/a).

Referencias

Gauthier N., Exact expressions for the amplitudes and damped normal frequencies of a taut vibrating linear string of coupled masses. Eur. J. Phys. 29 (2008) N21-N29

Valores propios ω²	Vectores propios
$\frac{k}{m}$	(A₁₁, A₁₁)
$3 \frac{k}{m}$	(A₁₂, -A₁₂)

Valores propios ω²	Vectores propios
$\frac{2 k}{m} (1 - \frac{\sqrt{2}}{2})$	$(A_{11}, A_{11} \sqrt{2}, A_{11})$
$\frac{2 k}{m}$	(A₁₂, 0, -A₁₂)
$\frac{2 k}{m} (1 + \frac{\sqrt{2}}{2})$	$(A_{13}, - A_{13} \sqrt{2}, A_{13})$

Valores propios ω²	Vectores propios
$\frac{k}{m} (2 - \sqrt{\frac{3 + \sqrt{5}}{2}}) = \frac{k}{m} (2 - \frac{\sqrt{5} + 1}{2})$	$(A_{11}, \frac{\sqrt{5} + 1}{2} A_{11}, \frac{\sqrt{5} + 1}{2} A_{11}, A_{11})$
$\frac{k}{m} (2 - \frac{\sqrt{5} - 1}{2})$	$(A_{12}, \frac{\sqrt{5} - 1}{2} A_{12}, - \frac{\sqrt{5} - 1}{2} A_{12}, - A_{12})$
$\frac{k}{m} (2 + \frac{\sqrt{5} - 1}{2})$	$(A_{13}, - \frac{\sqrt{5} - 1}{2} A_{13}, - \frac{\sqrt{5} - 1}{2} A_{13}, A_{13})$
$\frac{k}{m} (2 + \frac{\sqrt{5} + 1}{2})$	$(A_{14}, - \frac{\sqrt{5} + 1}{2} A_{14}, \frac{\sqrt{5} + 1}{2} A_{14}, - A_{14})$