• Inicio
• Oscilaciones
• Osciladores lineales

Un modelo para el coeficiente de restitución.

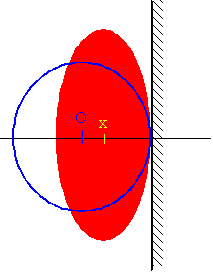En esta página se describe el impacto del balón sobre una pared rígida mediante un modelo mecánico simple.

Cuando el balón impacta sobre una pared rígida, supondremos que sobre el c.m. del balón actúan dos fuerzas :

• Una fuerza elástica proporcional al desplazamiento del c.m. de módulo kx, que tiende a restaurar al c.m. a su posición de equilibrio.
  
• Una fuerza de rozamiento λv, proporcional a la velocidad del c.m. y que da cuenta de la pérdida de energía del balón durante el impacto.

La ecuación del movimiento del c.m., es

ma=-kx-λv

o bien    

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=0{\omega }_{\text{0}}^{\text{2}}=\frac{k}{m}2\gamma =\frac{\lambda }{m}}$

Esta es la ecuación diferencial de las oscilaciones amortiguadas, donde ω₀²=k/m es la frecuencia propia o natural del sistema oscilante y γ =λ/(2m) es la constante de amortiguamiento.

Existen tres posibles soluciones de la ecuación diferencial, de acuerdo con las raíces de la ecuación característica.

Oscilaciones amortiguadas (γ<ω₀)

${\displaystyle \begin{array}{l}x=A\exp (-\gamma t)\sin (\omega t+\varphi ){\omega }^2={\omega }_0^2-{\gamma }^2\\ v=\frac{dx}{dt}=-\gamma A\exp (-\gamma t)\sin (\omega t+\varphi )+A\exp (-\gamma t)\omega \cos (\omega t+\varphi )\end{array}}$

Las condiciones iniciales determinan los valores de la amplitud inicial A y de la fase inicial φ. En nuestro caso son: t=0, x=0, y v=v₀.

${\displaystyle \begin{array}{l}x=\frac{v_0}{\omega }\exp (-\gamma t)\sin (\omega t)\\ v=\frac{dx}{dt}=-\gamma \frac{v_0}{\omega }\exp (-\gamma t)\sin (\omega t)+v_0\exp (-\gamma t)\cos (\omega t)\end{array}}$

Esta ecuación nos da la posición y velocidad del c.m. del balón deformado en función del tiempo.

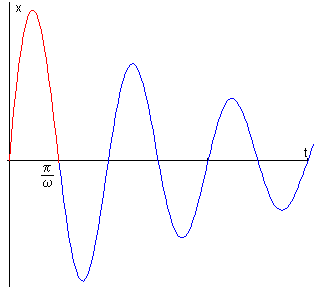
La figura nos muestra la representación gráfica de la posición del c.m. del balón en función del tiempo. Después de haber completado un semiperiodo de oscilación P/2=π/ω, (línea de color rojo) el c.m. del balón se aleja de la pared con una velocidad v dada por

${\displaystyle v=-v_0\exp \left(\frac{-\gamma \pi }{\omega }\right)}$

Se define el coeficiente de restitución e como el cociente entre la velocidad final v tras el choque entre la velocidad inicial v₀ justamente antes del choque con la pared.

${\displaystyle e=\exp \left(\frac{-\gamma \pi }{\omega }\right)}$

Podemos comprobar, que el coeficiente de restitución depende de dos parámetros que describen nuestro modelo simplificado, la frecuencia de la oscilación amortiguada y la constante de amortiguamiento.

Como podemos apreciar, si la constante de amortiguamiento es cero, γ=0, no hay rozamiento interno entre las diversas partes del balón, no hay pérdidas de energía, el choque es perfectamente elástico, y e=1.

Oscilación crítica (γ=ω₀)

La solución de la ecuación diferencial es

${\displaystyle x=(At+B)\exp (-\gamma t)}$

Con las condiciones iniciales antes mencionadas: t=0, x=0, v=v₀. se transforma en

${\displaystyle v=v_{0}t\exp (-\gamma t)}$

El c.m. del balón retorna a la posición de partida después de un tiempo teóricamente infinito, es decir, el balón no rebota, la velocidad final es cero, el coeficiente de restitución es cero, e=0.

Oscilación sobreamortiguada (γ>ω₀)

La solución de la ecuación diferencial es

${\displaystyle x=\left(A·e^{-\beta t}+B·e^{\beta t}\right)\exp (-\gamma t){\beta }^{\text{2}}={\gamma }^2-{\omega }_0^2}$

Con las condiciones iniciales antes mencionadas se transforma en

${\displaystyle x=\frac{v_0}{\beta }\exp (-\gamma t)\text{sinh}(\beta t)}$

El c.m. del balón retorna a la posición de partida después de un tiempo teóricamente infinito, es decir, el balón no rebota, la velocidad final es cero, el coeficiente de restitución es cero, e=0.

Actividades

Fijaremos la frecuencia propia ω₀ en el valor 100, permitiéndonos variar, la constante de amortiguamiento γ en el intervalo de 0 (choques elásticos) a 150.

Oscilaciones amortiguadas

Se introduce

• la constante de amortiguamiento (menor que 100, del orden de 10).
• la velocidad inicial (entre 1 y 10).

Se pulsa el botón titulado Empieza

1. Se anota el valor de la velocidad final después del rebote.
2. Se ensaya otras situaciones, cambiando la velocidad inicial pero sin modificar la constante de amortiguamiento.
3. Se comprueba que el cociente entre la velocidad final e inicial es constante. Trazar un gráfico y representar en el eje de ordenadas la velocidad final y el el eje de abscisas la velocidad inicial.

Oscilaciones críticas y sobreamortiguadas

• Observamos la deformación del balón en el caso que corresponde a oscilación crítica (γ=100),
• y otro que corresponda a una oscilación sobreamortiguada (γ>100).

RestitucionApplet aparecerá en un explorador compatible con JDK 1.1.

Curso Interactivo de Física en Internet © Ángel Franco García