Oscilaciones de un cuerpo que rueda sobre superficie cóncava.

En la página titulada "Movimiento sobre una superficie cóncava en forma de cicloide" demostramos que una partícula que desliza sin rozamiento sobre una superficie cóncava en forma de cicloide describe un Movimiento Armónico Simple cuya frecuencia angular es ω²=g/(4R). Vamos a demostrar que un cuerpo que rueda sin deslizar sobre una superficie cóncava describe también un Movimiento Armónico Simple, cuya frecuencia y periodo calcularemos en esta página.

Movimiento de un cuerpo que rueda sobre una superficie cóncava

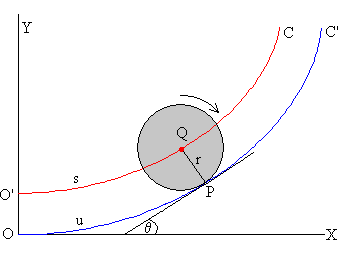
En la figura, se muestra la curva C’ sobre la que rueda el cuerpo redondo de radio r y la curva C que describe el centro de dicho cuerpo. La variable u mide la distancia OP a lo largo de la curva C’. Mientras el c.m. se desplaza s a lo largo de la curva C, el cuerpo gira un ángulo φ.

El ángulo θ mide la pendiente de la recta tangente a la curva C’ en P

La ecuación del movimiento

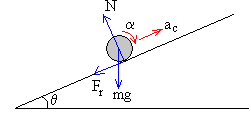
Las fuerzas sobre el cuerpo:

El peso mg
La reacción N de la superficie C’ en el punto de contacto P
La fuerza de rozamiento F_r

Formulamos las ecuaciones del movimiento

Movimiento de traslación del centro de masas

-mg·sinθ -F_r=ma_c

Movimiento de rotación alrededor de un eje que pasa por el centro de masas

F_r·r=I_c·α

Para un cuerpo redondo (aro, cilindro o esfera) de masa m y de radio r y cuyo momento de inercia I_c=k·mr² siendo k=1 para un cuerpo en forma de un aro, k=1/2 para un cilindro o disco, y k=2/5 para una esfera.

a_c+krα=-g·sinθ (1)

Finalmente, nos queda la condición de que el cuerpo rueda sin deslizar, que como demostraremos más adelante es

a_c=α ·r

La ecuación del camino

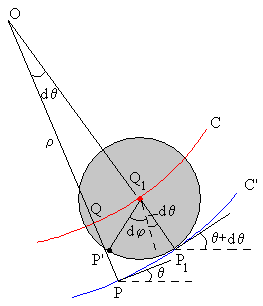En la figura, vemos que en un intervalo de tiempo comprendido entre los instantes t y t+dt,

el punto de contacto P se ha movido la distancia PP₁= du a lo largo de la curva C’,
el c.m. se ha movido la distancia QQ₁=ds a lo largo de la curva C.

Si trazamos las tangentes a la curva C’ en los puntos P y P₁ y las normales a dichas direcciones, vemos que se cortan en un punto O denominado centro de curvatura, la distancia entre dicho punto y P o P₁ se denomina radio de curvatura ρ.

Movimiento de traslación del cuerpo.

El ángulo que forman las rectas tangentes dθ es igual al ángulo que forman las direcciones normales.

El arco PP₁ es igual al producto del radio OP por el ángulo comprendido dθ.

du=ρ· dθ

El arco QQ₁ es igual al producto del radio OQ por el ángulo comprendido dθ.

ds=(ρ-r)· dθ

Movimiento de rotación del cuerpo.

Ahora, nos fijamos en el movimiento de rotación en el intervalo de tiempo comprendido entre los instantes t y t+dt

Como el cuerpo rueda sin deslizar, la longitud del arco PP₁=P₁P’=du. Como la pendiente de la curva se ha incrementado en dθ, el ángulo girado por el cuerpo en dicho intervalo dt de tiempo es

$d ϕ = \frac{P_{1} P'}{r} - d θ = \frac{d u}{r} - d θ$

Eliminando dθ, tenemos las relaciones

$d s = (1 - \frac{r}{ρ}) d u d ϕ = \frac{d s}{r}$

Esta última, es equivalente a la relación entre aceleraciones a_c=α ·r

La ecuación del movimiento (1) la podemos escribir en forma diferencial

$\begin{array}{l} \frac{d^{2} s}{d t^{2}} + k r \frac{d^{2} ϕ}{d t^{2}} = - g sin θ \\ \frac{d^{2} s}{d t^{2}} = - \frac{g}{k + 1} sin θ \end{array}$

El c.m. describe un MAS si la aceleración d²s/dt² es proporcional al desplazamiento s y de signo contrario a éste. Si escribimos

$sin θ = \frac{s}{4 R}$

donde R es una constante con dimensiones de longitud que no es el radio r del cuerpo como veremos más adelante. El c.m. describe un MAS

$\frac{d^{2} s}{d t^{2}} + \frac{g}{4 R (k + 1)} s = 0$

de frecuencia angular y periodo

$ω^{2} = \frac{g}{4 R (k + 1)} P = 2 π \sqrt{\frac{4 R (k + 1)}{g}}$

Si tomamos como radio R del disco que genera la cicloide la unidad (1 m), y g=9.8 m/s². Los periodos de las oscilaciones son respectivamente

Cuerpo	k	Periodo P (s)
aro	1	5.68
cilindro	1/2	4.92
esfera	2/5	4.75

Ecuación de la curva C que guía el c.m. del cuerpo

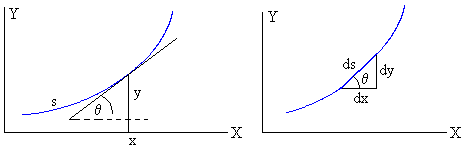
s=4R·sinθ
ds=4R·cosθ·dθ

dx=ds·cosθ=4Rcos²θ·dθ=2R(1+cos2θ)·dθ
dy=ds·sinθ=4R·sinθ·cosθ·dθ=2R·sin2θ·dθ

Integrando x e y con las condiciones iniciales θ=0, x=0, y=r.

x=R(2θ+sin2θ)
y=r+ R(1-cos2θ)

Estas son las ecuaciones paramétricas de una cicloide

Ecuación de la curva C' sobre la que que rueda el cuerpo

ds=4R·cosθ·dθ. De la relación entre ds y du y como du=ρ·dθ

$\begin{array}{l} (1 - \frac{r}{ρ}) d u = 4 R \cos θ \cdot d θ \\ (1 - \frac{r}{ρ}) ρ \cdot d θ = 4 R \cos θ \cdot d θ \end{array}$

Obtenemos el valor del radio de curvatura ρ

ρ=r+4R·cosθ

La relación entre el desplazamiento infinitesimal du del punto P y la pendiente θ es

du=(r+4R·cosθ)·dθ

dx’=du·cosθ=(r·cosθ+4R·cos²θ)·dθ=(r·cosθ+2R·(1+cos2θ))·dθ
dy’=du·sinθ=(r·sinθ+4R· sinθ·cosθ)·dθ==(r·sinθ+2R· sin2θ)·dθ

Integrando x’ e y’ con las condiciones iniciales θ=0, x=0, y=0.

x’=r·sinθ+R(2θ+sin2θ)
y’=r(1-cosθ)+ R(1-cos2θ)

Esta no es la ecuación de una cicloide salvo que r→0

Comprobación

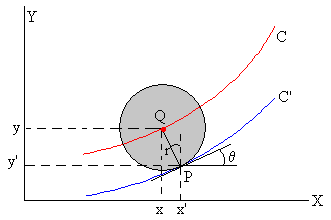
En la figura, vemos que al punto P(x’, y’) es un punto de la curva C’ le corresponde el punto Q(x, y) de la curva C. La relación entre x’ y x, y entre y e y’ es

x=x’-r·sinθ
y=y’+ r·cosθ

La curva C que describe el c.m. es una cicloide invertida (-π/2<θ< π/2) cuyo mínimo está en (0, r) y cuyo disco generador tiene un radio R. Sin embargo, la curva C’ sobre la que rueda el cuerpo sin deslizar no es una cicloide salvo que el radio del cuerpo sea r=0.

Movimiento Armónico Simple

Cuando un cuerpo describe un MAS su desplazamiento (en este caso el arco s) se expresa en función del tiempo de acuerdo con la ecuación.

s=A·sin(ω t+φ )

v_c=ω s₀·cos(ω t+φ)

Donde la amplitud A y la fase inicial φ se determina a partir de las condiciones iniciales, en nuestro caso t=0, s=s₀, v_c=0. La rueda parte de la posición s₀ con velocidad inicial cero.

s=s₀·sin(ω t+π/2)=s₀·cos(ω ·t)

La velocidad v_c del c.m. de la rueda se obtendrá derivando s respecto del tiempo

v_c=-ω s₀·sin(ω t)

Balance energético

El balance energético es similar al que efectuamos al estudiar el movimiento de un cuerpo que baja rodando por un plano inclinado.

Cuando la rueda se encuentra en la posición dada por el arco s a lo largo de la cicloide, o a una altura y sobre el origen. La energía potencial es

$\begin{array}{l} E_{p} = m g y = m g R (1 - \cos 2 θ) = 2 m g R \sin^{2} θ = \frac{m g}{8 R} s^{2} \\ E_{p} = \frac{m g}{8 R} s_{0}^{2} \cos^{2} (ω t) \end{array}$

La energía cinética es la suma de la energía cinética de traslación del c.m. y de rotación alrededor de un eje que pasa por c.m.

$E_{k} = \frac{1}{2} m v_{c}^{2} + \frac{1}{2} I_{c} ω^{2} = \frac{1}{2} m (k + 1) ω^{2} s_{0}^{2} \sin^{2} (ω t) = \frac{m g}{8 R} s_{0}^{2} \sin^{2} (ω t)$

donde se ha tenido en cuenta la relación entre ambas velocidades v_c=ω ·r para que ruede sin deslizar.

La suma de la energía cinética E_k y potencial E_p es constante e igual a

$E = E_{k} + E_{p} = \frac{m g}{8 R} s_{0}^{2}$

Actividades

Se introduce

La posición inicial s₀ (longitud inicial del arco de la cicloide), actuando en la barra de desplazamiento titulada Arco inicial
El cuerpo que rueda, en el control de selección titulado Cuerpo.
El radio del disco que genera la cicloide se ha fijado en R=1 m, con ello queda fijada la forma de la superficie cóncava
El radio del cuerpo redondo se ha fijado en r=0.4 m

Se pulsa el botón titulado Inicio, y a continuación Empieza.

Observamos como el cuerpo rueda sin deslizar por un camino en forma de cicloide. La ecuación del movimiento es

s=s₀·cos(ω ·t)

Donde s es la longitud del arco de cicloide y ω la frecuencia angular del MAS

En la parte superior, se muestra el balance energético en un diagrama en forma de tarta. La energía potencial E_p y la energía cinética E_k como suma de la energía cinética de traslación del c.m. y de rotación alrededor de un eje que pasa por el c.m.

Para realizar otro ensayo, se pulsa el botón Inicio, se modifican los parámetros (se elige otro cuerpo o se cambia la posición inicial de partida) y se pulsa el botón titulado Empieza.

CinemaApplet1 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Gillespie D. T. Simple harmonic motion of a round body rolling on a concave curve. Am. J. Phys. 52 (2) February 1984, pp. 180-182.