• Inicio
• Fenómenos de transporte
• Conducción del calor

Conducción del calor (II)

En la página anterior, examinamos la distribución de temperaturas de una barra metálica en un determinado instante t, cuando se proporcionan los datos de:

• El metal con el que está hecha la barra, o el valor del parámetro α=K/(ρc)

• La temperatura inicial de la barra en el instante t=0.

• Las temperaturas fijas en los extremos

En esta página, vamos a fijarnos en la evolución temporal de la temperatura de un punto x de la barra metálica y a examinar el papel que juegan la capacidad calorífica y la conductividad térmica en la conducción del calor.

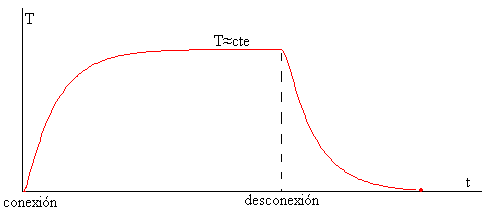
El extremo libre de una barra metálica de longitud L, está a una temperatura fija T₀, por ejemplo, la de un baño que contenga una mezcla de hielo y agua. En el otro extremo, hay una fuente de calor de potencia dQ/dt watios. En un punto x de la barra se coloca un termómetro. Cuando se conecta la fuente de calor, observamos como la temperatura en dicho punto, va creciendo hasta que toma un valor constante T después de cierto tiempo, teóricamente infinito. Se ha establecido el estado estacionario.

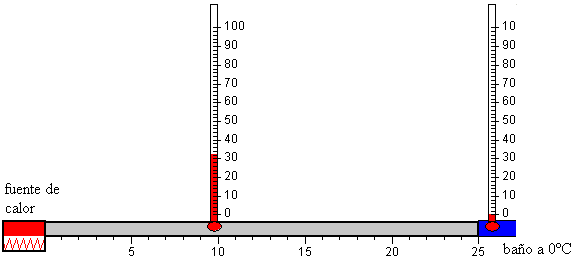
Retiramos la fuente de calor, los dos extremos de la barra x=0, y x=L están a la temperatura fija T₀ del baño. Observamos como la temperatura de dicho punto de la barra va descendiendo hasta que alcanza la temperatura T₀ de baño al cabo de un cierto tiempo, teóricamente infinito.

El estado estacionario

La ecuación diferencial que describe la conducción térmica

${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}\alpha =\frac{K}{\rho c}}$

• ρ es la densidad

• c es el calor específico

• K es la conductividad térmica

En el estado estacionario la temperatura de los puntos de la barra no cambia con el tiempo, ∂T/∂t=0, ∂T/∂x es constante, de acuerdo a la ley de Fourier

${\displaystyle \frac{\partial T}{\partial x}=-\frac{\dot{Q}}{SK}\dot{Q}=\frac{dQ}{dt}}$

El signo menos indica que la temperatura disminuye a lo largo de la barra: el foco caliente está en x=0, y el foco frío en x=L.

• S es el área de la sección trasversal de la barra 

• dQ/dt es la potencia de la fuente de calor colocada en uno de los extremos de la barra.

• K una constante característica del material denominada conductividad térmica.

En el estado estacionario t→∞

${\displaystyle \begin{array}{l}{\displaystyle \underset{L}{\overset{x}{\int }}-\frac{\dot{Q}}{KS}dx}={\displaystyle \underset{T_0}{\overset{T}{\int }}dT}\\ T(x,\infty )=T_0+\frac{\dot{Q}}{KS}(L-x)\end{array}}$

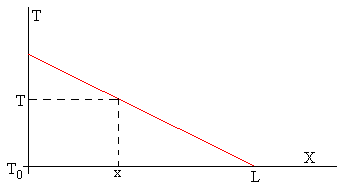
Conociendo la potencia de la fuente de calor, la temperatura fija T₀ del extremo x=L y la temperatura T de dicho punto x de la barra podemos determinar el coeficiente K de conductividad térmica.

Ejemplo:

• La potencia de la fuente de calor colocada en un extremo  de la barra es 4.0 W

• El otro extremo de la barra, se mantiene a la temperatura de un baño consistente en una mezcla de hielo y agua T₀=0 ºC

• La barra metálica es un cilindro de L=25 cm de longitud y r=5 mm de radio

El termómetro se coloca en la posición x=3 cm, y mide una temperatura máxima de T=53.6 ºC un tiempo suficientemente grande después de haber conectado la fuente de calor.

${\displaystyle 53.6=0+\frac{4}{K(\pi ·{0.005}^2)}(0.25-0.03)K=209.0\text{W/(m·K)}}$

Se conecta la fuente de calor

La temperatura en cualquier punto x a lo largo de la barra, en un instante determinado, T(x, t) es una combinación de dos términos, la que corresponde al régimen permanente T(∞, x) más la del régimen transitorio.

${\displaystyle T(x,t)=T_0+\frac{\dot{Q}}{KS}(L-x)+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}\sin \left({\omega }_{n}x+{\delta }_n\right)}$

Condiciones de contorno:

• En x=L, T(L, t)=T₀, temperatura fija del extremo derecho de la barra

${\displaystyle 0={\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}\sin \left({\omega }_{n}L+{\delta }_n\right){\omega }_{n}L+{\delta }_n=n\pi }$

• En x=0, la potencia de la fuente calor dQ/dt=cte es constante, para todo t, que de acuerdo a la ley de Fourier equivale a

${\displaystyle {\left(\frac{\partial T}{\partial x}\right)}_{x=0}=-\frac{\dot{Q}}{SK}\dot{Q}=\frac{dQ}{dt}}$

Derivamos la expresión de la temperatura T(x,t) respecto de x

${\displaystyle \begin{array}{l}\frac{\partial T}{\partial x}=-\frac{\dot{Q}}{KS}+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}{\omega }_n\cos \left({\omega }_{n}x+{\delta }_n\right)\\ -\frac{\dot{Q}}{KS}=-\frac{\dot{Q}}{KS}+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}{\omega }_n\cos \left({\delta }_n\right)\\ 0={\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}{\omega }_n\cos \left({\delta }_n\right){\delta }_n=\frac{\pi }{2}\end{array}}$

Hemos determinado la fase δ_n, ahora las frecuencias angulares ω_n valen

${\displaystyle {\omega }_n=\frac{(2n-1)\pi }{2L}}$

El régimen variable general de temperaturas de la barra es

${\displaystyle T(x,t)=T_0+\frac{\dot{Q}}{KS}(L-x)+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp \left(-\alpha \frac{{\left(2n-1\right)}^2{\pi }^2}{4L^2}t\right)}\cos \left(\frac{(2n-1)\pi }{2L}x\right)}$

Solamente, queda por determinar los coeficientes a_n, lo que se conseguirá identificando esta solución con la distribución inicial de temperaturas en la barra T(x, 0)=T₀ en el instante t=0.

${\displaystyle \begin{array}{l}T(x\mathrm{,0})=T_0=T_0+\frac{\dot{Q}}{KS}(L-x)+{\displaystyle \sum _{n=1}^{\infty }{a}_n}\cos \left(\frac{(2n-1)\pi }{2L}x\right)\\ f(x)={\displaystyle \sum _{n=1}^{\infty }{a}_n}\cos \left(\frac{(2n-1)\pi }{2L}x\right)f(x)=-\frac{\dot{Q}}{KS}(L-x)\end{array}}$

Hacemos la siguiente integración .

${\displaystyle {\displaystyle \underset{0}{\overset{L}{\int }}f(x)\cos }\left(\frac{(2m-1)\pi }{2L}x\right)dx={\displaystyle \sum _{n=1}^{\infty }{a}_n}{\displaystyle \underset{\text{0}}{\overset{\text{L}}{\int }}\cos \left(\frac{(2n-1)\pi }{2L}x\right)\cos \left(\frac{(2m-1)\pi }{2L}x\right)}dx}$

Hacemos el cambio de variable z=πx/L, dz= πdx/L

${\displaystyle \begin{array}{l}\frac{L}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}f\left(\frac{L}{\pi }z\right)\cos }\left(\frac{(2m-1)}{2}z\right)dz=\frac{L}{\pi }{\displaystyle \sum _{n=1}^{\infty }{a}_n}{\displaystyle \underset{\text{0}}{\overset{\pi }{\int }}\cos \left(\frac{(2n-1)}{2}z\right)\cos \left(\frac{(2m-1)}{2}z\right)}dz\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}f\left(\frac{L}{\pi }z\right)\cos }\left(m_{\frac{1}{2}}z\right)dz={\displaystyle \sum _{n=1}^{\infty }{a}_n}{\displaystyle \underset{\text{0}}{\overset{\pi }{\int }}\cos \left(n_{\frac{1}{2}}z\right)\cos \left(m_{\frac{1}{2}}z\right)}dz{m}_{\frac{1}{2}}=\frac{(2m-1)}{2}{n}_{\frac{1}{2}}=\frac{(2n-1)}{2}\end{array}}$

Integramos dos veces por partes

${\displaystyle \begin{array}{l}{m}_{\frac{1}{2}}\ne n_{\frac{1}{2}}\\ {\displaystyle \underset{\text{0}}{\overset{\pi }{\int }}\cos \left(n_{\frac{1}{2}}z\right)\cos \left(m_{\frac{1}{2}}z\right)}dz={\frac{m_{\frac{1}{2}}\cos \left(n_{\frac{1}{2}}z\right)\sin \left(m_{\frac{1}{2}}z\right)-n_{\frac{1}{2}}\cos \left(m_{\frac{1}{2}}z\right)\sin \left(n_{\frac{1}{2}}z\right)}{m_{\frac{1}{2}}^2-n_{\frac{1}{2}}^2}|}_0^{\pi }=0\\ m_{\frac{1}{2}}=n_{\frac{1}{2}}\\ {\displaystyle \underset{\text{0}}{\overset{\pi }{\int }}{\cos }^2\left(n_{\frac{1}{2}}z\right)}dz=\frac{1}{2}{\left(z+\frac{\sin \left(2n_{\frac{1}{2}}z\right)}{2n_{\frac{1}{2}}}\right)|}_0^{\pi }=\frac{\pi }{2}\end{array}}$

De acuerdo con estos resultados, despejamos los coeficientes a_n del desarrollo en serie

${\displaystyle \begin{array}{l}{a}_n=\frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}f\left(\frac{L}{\pi }z\right)\cos }\left(n_{\frac{1}{2}}z\right)dz\\ f\left(\frac{L}{\pi }z\right)=-\frac{\dot{Q}}{KS}\left(L-\frac{L}{\pi }z\right)=-\frac{\dot{Q}L}{KS}\left(1-\frac{z}{\pi }\right)=a+bza=-\frac{\dot{Q}L}{KS}b=\frac{\dot{Q}L}{KS\pi }\end{array}}$

Integramos de nuevo, por partes

${\displaystyle \begin{array}{l}{a}_n=\frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}\left(a+bz\right)\cos }\text{(}{n}_{\frac{1}{2}}z\text{) }dz=\\ \frac{\text{2}}{\pi }{\left\{\frac{a}{n_{\frac{1}{2}}}\sin \left(n_{\frac{1}{2}}z\right)+b\left(\frac{z}{n_{\frac{1}{2}}}\sin \left(n_{\frac{1}{2}}z\right)+\frac{1}{n_{\frac{1}{2}}^2}\cos \left(n_{\frac{1}{2}}z\right)\right)\right\}}_0^{\pi }=\\ \frac{\text{2}}{\pi }{\left\{\frac{a+bz}{n_{\frac{1}{2}}}\sin \left(n_{\frac{1}{2}}z\right)+\frac{b}{n_{\frac{1}{2}}^2}\cos \left(n_{\frac{1}{2}}z\right)\right\}}_0^{\pi }=-\frac{2b}{\pi n_{\frac{1}{2}}^2}=-\frac{8\dot{Q}L}{KS{\pi }^2{\left(2n-1\right)}^2}\end{array}}$

Fijarse que a+bπ=0

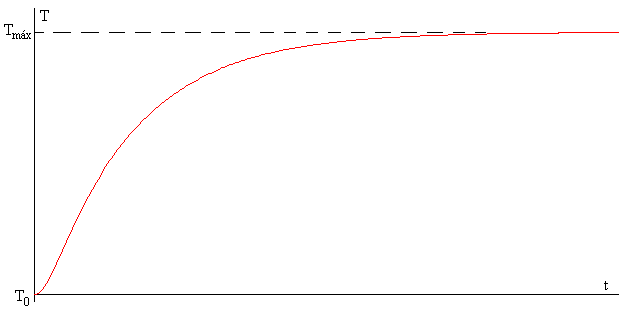
Así, la temperatura en cualquier punto de la barra x, en un instante t, se compone de la suma de un término proporcional a x, y de una serie rápidamente convergente que describe el estado transitorio.

${\displaystyle T(x,t)=T_0+\frac{\dot{Q}}{KS}(L-x)-\frac{8\dot{Q}L}{KS{\pi }^2}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\left(2n-1\right)}^2}\exp \left(-\alpha \frac{{\left(2n-1\right)}^2{\pi }^2}{4L^2}t\right)}\cos \left(\frac{(2n-1)\pi }{2L}x\right)}$

La temperatura en un punto x, alcanza al cabo de un cierto tiempo, teóricamente infinito, un valor constante, tal como se muestra en la figura.

${\displaystyle T(x,\infty )=T_0+\frac{\dot{Q}}{KS}(L-x)}$

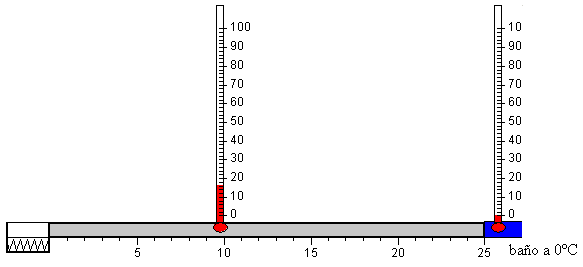
Se desconecta la fuente de calor

Se desconecta la fuente de calor, ponemos el reloj a cero, t=0.

La distribución inicial de temperaturas corresponde al estado estacionario de la etapa anterior.

${\displaystyle T(x\mathrm{,0})=T_0+\frac{\dot{Q}}{KS}(L-x)}$

El estado estacionario se alcanza después de un tiempo infinito. Todos los puntos de la barra tienen la misma temperatura del baño situado en el extremo derecho de la barra T(x, ∞)=T₀.

La temperatura en cualquier punto x a lo largo de la barra, en un instante determinado, T(x, t) es una combinación de dos términos, la que corresponde al régimen permanente T(∞, x) más la del régimen transitorio.

${\displaystyle T(x,t)=T_0+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}\sin \left({\omega }_{n}x+{\delta }_n\right)}$

Condiciones de contorno:

• En x=L, T(L, t)=T₀, temperatura fija del extremo derecho de la barra

${\displaystyle 0={\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}\sin \left({\omega }_{n}L+{\delta }_n\right){\omega }_{n}L+{\delta }_n=n\pi }$

• En x=0, se ha desconectado la fuente calor dQ/dt=0, para todo t, que de acuerdo a la ley de Fourier equivale a

${\displaystyle {\left(\frac{\partial T}{\partial x}\right)}_{x=0}=0}$

Derivamos la expresión de la temperatura T(x,t) respecto de x

${\displaystyle \begin{array}{l}\frac{\partial T}{\partial x}={\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}{\omega }_n\cos \left({\omega }_{n}x+{\delta }_n\right)\\ 0={\displaystyle \sum _{n=1}^{\infty }{a}_n\exp (-\alpha {\omega }_n^{2}t)}{\omega }_n\cos \left({\delta }_n\right){\delta }_n=\frac{\pi }{2}\end{array}}$

Hemos determinado la fase δ_n, ahora las frecuencias angulares ω_n valen

${\displaystyle {\omega }_n=\frac{(2n-1)\pi }{2L}}$

El régimen variable general de temperaturas de la barra es la suma del estado estacionario más el estado transitorio

${\displaystyle T(x,t)=T_0+{\displaystyle \sum _{n=1}^{\infty }{a}_n\exp \left(-\alpha \frac{{\left(2n-1\right)}^2{\pi }^2}{4L^2}t\right)}\cos \left(\frac{(2n-1)\pi }{2L}x\right)}$

Solamente, queda por determinar los coeficientes a_n, lo que se conseguirá identificando esta solución con la distribución inicial de temperaturas T(x, 0) en la barra

${\displaystyle \begin{array}{l}{T}_0+\frac{\dot{Q}}{KS}(L-x)=T_0+{\displaystyle \sum _{n=1}^{\infty }{a}_n}\cos \left(\frac{(2n-1)\pi }{2L}x\right)\\ \frac{\dot{Q}}{KS}(L-x)={\displaystyle \sum _{n=1}^{\infty }{a}_n}\cos \left(\frac{(2n-1)\pi }{2L}x\right)\end{array}}$

Tenemos que calcular los coeficientes a_n de la función

${\displaystyle f(x)=\frac{\dot{Q}}{KS}(L-x)}$

Haciendo el cambio de variable z=πx/L, la función f(z) se escribe

${\displaystyle f\left(\frac{L}{\pi }z\right)=\frac{\dot{Q}L}{KS}\left(1-\frac{z}{\pi }\right)=a+bza=\frac{\dot{Q}L}{KS}b=-\frac{\dot{Q}L}{KS\pi }}$

Calculamos los coeficientes a_n de forma similar al caso anterior

${\displaystyle a_n=\frac{2}{\pi }{\displaystyle \underset{0}{\overset{\pi }{\int }}f\left(\frac{L}{\pi }z\right)\cos }\text{(}{n}_{\frac{1}{2}}z\text{) }dz=-\frac{2b}{\pi n_{\frac{1}{2}}^2}=\frac{8\dot{Q}L}{KS{\pi }^2{\left(2n-1\right)}^2}}$

El resultado es.

${\displaystyle T(x,t)=T_0+\frac{8\dot{Q}L}{KS{\pi }^2}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{{\left(2n-1\right)}^2}\exp \left(-\alpha \frac{{\left(2n-1\right)}^2{\pi }^2}{4L^2}t\right)}\cos \left(\frac{(2n-1)\pi }{2L}x\right)}$

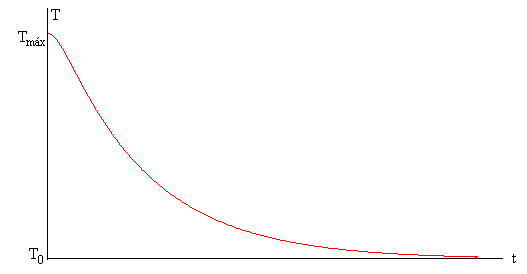
En la figura se muestra, cómo la temperatura de un punto x de la barra, estudiado en el apartado anterior, va disminuyendo con el tiempo hasta que alcanza la temperatura del baño térmico T₀.

Actividades:

Se introduce

• La potencia de la fuente de calor en W, actuando en la barra de desplazamiento titulada Potencia

• La conductividad térmica K, en W/(m·K), en el control de edición titulado Conductividad

• El calor específico c en J/(kg·K), en el control de edición titulado Calor esp.

• La densidad del material se ha fijado en ρ=5000 kg/m³

• La longitud de la barra se ha fijado en L=25 cm

• El radio de la sección trasversal se ha fijado en r=5 mm

• La temperatura del otro extremo de la barra se ha fijado en T₀=0ºC

Se pulsa el botón titulado Nuevo.

• Se desplaza el termómetro, arrastrándolo con el puntero del ratón a cualquier posición 2<x<22 cm de la barra.

• Se establece la escala horizontal del eje de tiempos, en el control de selección titulado Escala t.

Se pulsa el botón titulado Conecta.

Observamos como la temperatura del termómetro se incrementa.

Si se activa la casilla titulada Gráfica, se obtiene la representación gráfica de la temperatura que marca el termómetro en función del tiempo.

Cuando la temperatura alcance aproximadamente, su valor máximo constante (estado estacionario), el programa interactivo nos lo indica mediante un mensaje, se puede pulsar el mismo botón titulado ahora, Desconecta.

La temperatura del termómetro va disminuyendo rápidamente, hasta que alcanza el valor de la temperatura del baño T₀=0 ºC.

Se sugiere al lector que

• Cambie la posición del termómetro en la barra manteniendo fijas la conductividad K y el calor específico c.

• Modifique la potencia de la fuente y anote la temperatura máxima que marca el termómetro en el estado estacionario.

• Manteniendo fija la potencia y la posición del termómetro, cambie el calor específico c manteniendo fijo el valor de la conductividad térmica K.

• Manteniendo fija la potencia y la posición del termómetro, cambie la conductividad térmica K manteniendo fijo el valor del calor específico c.

TermicoApplet3 aparecerá en un explorador compatible con JDK 1.1.

Arrastre con el puntero del ratón el extremo inferior el termómetro de la izquierda

Referencias

Fox J. N., McMaster R. H., Measurement of the thermal properties of a metal using a relaxation method. Am. J. Phys. 43 (12) December 1975, pp. 1083-1086

Curso Interactivo de Física en Internet © Ángel Franco García