• Inicio
• Unidades y medidas
• Medidas

Medidas indirectas

En muchos casos, el valor experimental de una magnitud se obtiene, de acuerdo a una determinada expresión matemática, a partir de la medida de otras magnitudes de las que depende. Se trata de conocer el error en la magnitud derivada a partir de los errores de las magnitudes medidas directamente.

Funciones de una sola variable

Si se desea calcular el índice de refracción n de un vidrio midiendo el ángulo crítico θ, tenemos que n=1/senθ. Si medimos el ángulo θ es fácil calcular el índice de refracción n. Pero si conocemos el error de la medida del ángulo, necesitamos conocer el error del índice de refracción.

Sea una función y=y(x). Como se aprecia en la figura, si el error Δx es pequeño. El error Δy se calcula del siguiente modo

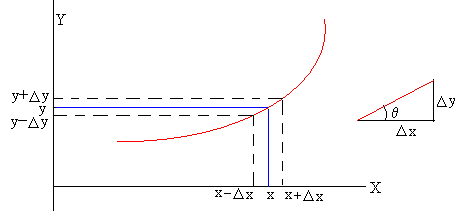
Δy=tanθ·Δx

Pero tanθ es la pendiente de la recta tangente a al curva en el punto de abscisa x

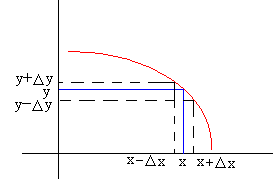
Como la pendiente puede ser positiva, si la función es creciente o negativa si la función es decreciente, en general tendremos que

${\displaystyle \Delta y=\left|f\text{'}(<x>)\right|\Delta x}$

Sea y=cos x

Sea x=20±3 º,

y=cos20=0.9397

El error Δx=0.05 rad

Δy=|sin20|·0.05=0.02

y=0.94±0.02

Un ejemplo importante y frecuente en el laboratorio sobre las medidas indirectas es el siguiente: Supongamos que queremos medir el periodo P de un oscilador, es decir, el tiempo que tarda en efectuar una oscilación completa, y disponemos de un cronómetro que aprecia las décimas de segundo, 0.1 s. Medimos el tiempo que tarda en hacer 10 oscilaciones, por ejemplo 4.6 s, dividiendo este tiempo entre 10 resulta P=0.46 s, que es el periodo "medio".

${\displaystyle P=\frac{t}{10}\Delta P=\frac{\Delta t}{10}}$

 Obtenemos para el error DP=0.01 s. Por tanto, la medida la podemos expresar como

P=0.46±0.01 s

Es evidente, que podemos aumentar indefinidamente la resolución instrumental para medir P aumentando el número de periodos que incluimos en la medida directa de t. El límite está en nuestra paciencia y la creciente probabilidad de cometer errores cuando contamos el número de oscilaciones. Por otra parte, el oscilador no se mantiene con la misma amplitud indefinidamente, sino que se para al cabo de un cierto tiempo.

Función de varias variables

La magnitud y viene determinada por la medida de varias magnitudes p, q, r, etc., con la que está ligada por la función

 y=f(p, q, r ...).

El error de la magnitud y viene dado por la siguiente expresión.

${\displaystyle \Delta y=\sqrt{{\left(<\frac{\partial f}{\partial p}>\Delta p\right)}^2+{\left(<\frac{\partial f}{\partial q}>\Delta q\right)}^2+{\left(<\frac{\partial f}{\partial r}>\Delta r\right)}^2+\mathrm{...}}}$

Casos más frecuentes

${\displaystyle \begin{array}{l}z=x+y\Delta z=\sqrt{\Delta x^2+\Delta y^2}\\ z=x-y\Delta z=\sqrt{\Delta x^2+\Delta y^2}\\ z=x\cdot y\frac{\Delta z}{z}=\sqrt{{\left(\frac{\Delta x}{x}\right)}^2+{\left(\frac{\Delta y}{y}\right)}^2}\\ z=\frac{x}{y}\frac{\Delta z}{z}=\sqrt{{\left(\frac{\Delta x}{x}\right)}^2+{\left(\frac{\Delta y}{y}\right)}^2}\end{array}}$

La medida de los lados de un rectángulo son 1.53±0.06 cm, y 10.2±0.1 cm, respectivamente. Hallar el área del rectángulo y el error de la medida indirecta.

El área es z=1.53×10.2=15.606 cm²

El error relativo del área Dz/z se obtiene aplicando la fórmula del producto de dos magnitudes.

${\displaystyle \begin{array}{l}\frac{\Delta z}{z}=\sqrt{{\left(\frac{0.06}{1.53}\right)}^2+{\left(\frac{0.1}{10.2}\right)}^2}=0.0404422504\\ \Delta z=\left(1.53\cdot 10.2\right)\cdot 0.0404422504=0.63083\end{array}}$

El error absoluto con una sola cifra significativa es 0.6. De acuerdo con la regla 3, la medida del área junto con el error y la unidad se escribirá como

15.6±0.6 cm²

Funciones de dos variables

Queremos calcular la aceleración de la gravedad g, midiendo el periodo P de un péndulo de longitud l

El periodo de un péndulo

${\displaystyle P=2\pi \sqrt{\frac{l}{g}}g=4{\pi }^2\frac{l}{P^2}}$

La expresión del error Δg de la variable dependiente g

${\displaystyle \begin{array}{l}\Delta g=\sqrt{{\left(4{\pi }^2\frac{1}{P^2}\Delta l\right)}^2+{\left(4{\pi }^2\frac{-2}{P^3}\Delta P\right)}^2}=4{\pi }^2\frac{l}{P^2}\sqrt{{\left(\frac{\Delta l}{l}\right)}^2+{\left(\frac{2\Delta P}{P}\right)}^2}\\ \frac{\Delta g}{g}=\sqrt{{\left(\frac{\Delta l}{l}\right)}^2+{\left(\frac{2\Delta P}{P}\right)}^2}\end{array}}$

Supongamos que medimos el periodo P y la longitud l del péndulo

P=1.396±0.004 s
l=92.9±0.1 cm

Calculamos la aceleración de la gravedad y el error

g=979.035 cm/s²
Δg=4.28

Expresamos correctamente la medida y el error de g

979±4 cm/s²

Ley de Snell de la refracción

${\displaystyle n=\frac{\sin i}{\sin r}}$

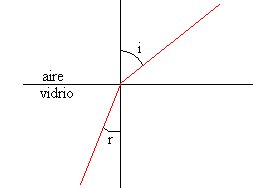
Cálculo del error en la medida del índice de refracción n.

${\displaystyle \frac{\Delta n}{n}=\sqrt{{\left(\frac{1}{\tan i}\Delta i\right)}^2+{\left(\frac{1}{\tan r}\Delta r\right)}^2}}$

Sea i=20±1 º y r=13±1 º

Se calcula el índice de refracción y el error

 n=1.52
Δn=0.136

Expresamos correctamente la medida y el error de n

n=1.5±0.1

Referencias

Dpto. de Física de la Materia Condensada. Cálculo de errores en las medidas. Universidad del País Vasco. Leioa (Vizcaya)

Taylor J. R. An Introduction to Error Analysis. The Study of Uncertainties in Physical Measurements. University Science Books (1982)

Curso Interactivo de Física en Internet © Ángel Franco García