La experiencia nos demuestra que cuando abrimos un frasco de perfume o de cualquier otro líquido volátil, percibimos su olor rápidamente en un recinto cerrado. Decimos que las moléculas del líquido después de evaporarse se difunden por el aire, distribuyéndose en todo el espacio circundante. Lo mismo ocurre si colocamos un terrón de azúcar en un vaso de agua, las moléculas de sacarosa se difunden por todo el agua. Estos y otros ejemplos nos muestran que para que tenga lugar el fenómeno de la difusión, la distribución espacial de moléculas no debe ser homogénea, debe existir una diferencia, o gradiente de concentración entre dos puntos del medio.

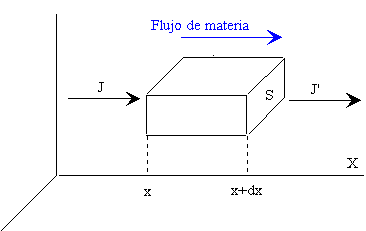
Supongamos que su concentración varía con la posición al lo largo del eje X. Llamemos J a la densidad de corriente de partículas, es decir, al número efectivo de partículas que atraviesan en la unidad de tiempo un área unitaria perpendicular a la dirección en la que tiene lugar la difusión. La ley de Fick afirma que la densidad de corriente de partículas es proporcional al gradiente de concentración

${\displaystyle J=-D\frac{\partial c}{\partial x}}$

La constante de proporcionalidad se denomina coeficiente de difusión D y es característico tanto del soluto como del medio en el que se disuelve.

La acumulación de partículas en la unidad de tiempo que se produce en el elemento de volumen S·dx es igual a la diferencia entre el flujo entrante JS, menos el flujo saliente J’S, es decir

${\displaystyle JS-J\text{'}S=\frac{\partial J}{\partial x}Sdx}$

La acumulación de partículas en la unidad de tiempo es

${\displaystyle (Sdx)\frac{\partial c}{\partial t}}$

Igualando ambas expresiones y utilizando la Ley de Fick se obtiene

${\displaystyle \frac{\partial }{\partial x}\left(D\frac{\partial c}{\partial x}\right)=\frac{\partial c}{\partial t}}$

Ecuación diferencial en derivadas parciales que describe el fenómeno de la difusión. Si el coeficiente de difusión D no depende de la concentración

${\displaystyle \frac{1}{D}\frac{\partial c}{\partial t}=\frac{{\partial }^{2}c}{\partial x^2}}$

Distribución inicial de masa en un plano

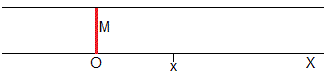
Vamos a considerar el problema de la difusión unidimensional de una masa M de soluto, distribuída inicialmente en un plano situado en el origen de un medio de extensión infinita.

La solución de la ecuación diferencial en derivadas parciales nos da la concentración en los puntos x del medio en cada instante de tiempo t>0.

${\displaystyle c(x,t)=\frac{M}{\sqrt{4\pi Dt}}\exp \left(\frac{-x^2}{4Dt}\right)}$

Esta ecuación describe la extensión por difusión de una cantidad de sustancia M depositada en el plano x=0

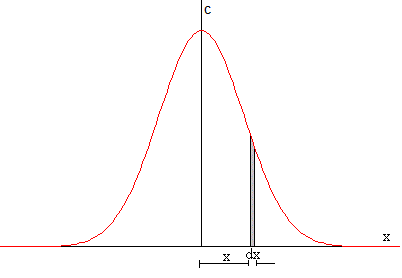
El área bajo la curva acampanada es la misma para todos las gráficas.

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}c(x,t)dx}=2{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{M}{2\sqrt{\pi Dt}}\exp \left(\frac{-x^2}{4Dt}\right)}dx=M}$

Para ello, se emplea el resultado de la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}=\frac{1}{2}\sqrt{\frac{\pi }{\alpha }}}$

>> syms x a positive;
>> int('exp(-a*x^2)',x,0,inf)
ans =pi^(1/2)/(2*a^(1/2))

Desplazamiento medio cuadrático

${\displaystyle <x^2>=\frac{1}{M}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{x}^2}c(x,t)dx=\frac{1}{\sqrt{\pi Dt}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp \left(\frac{-x^2}{4Dt}\right)}dx}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp (-\alpha x^2)dx}=\frac{1}{2\alpha }\left({-x\exp (-\alpha x^2)|}_0^{\infty }+{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}\right)=\frac{1}{4\alpha }\sqrt{\frac{\pi }{\alpha }}\\ <x^2>=\frac{1}{\sqrt{\pi Dt}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp \left(\frac{-x^2}{4Dt}\right)}dx=2Dt\end{array}}$

>> syms x a positive;
>> int('x^2*exp(-a*x^2)',x,0,inf)
ans =pi^(1/2)/(4*a^(3/2))

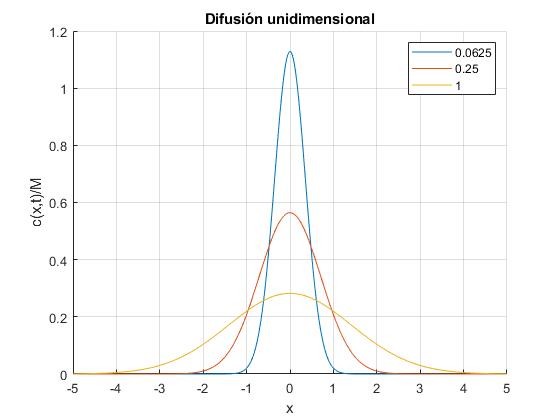
Representamos c(x,t)/M en función de x para tres valores del producto Dt: 1/16, 1/4 y 1

hold on
for t=[1/16,1/4,1] %producto Dt
    f=@(x) exp(-x.^2/(4*t))/sqrt(4*pi*t);
    fplot(f,[-5,5],'displayName',num2str(t))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('c(x,t)/M')
title('Difusión unidimensional')

En los dos ejemplos de difusión, de un gas en aire, o de un soluto en agua (líquido), se pone de manifiesto la relación entre el orden de magnitud del coeficiente de difusión (10^-4 y 10^-9, respectivamente) y la escala de longitud o de tiempo en el que transcurren ambos fenómenos.

Difusión de un gas en el aire

Se supondrán gases ideales. En esta aproximación, el coeficiente de difusión se mantiene constante y no varía con la concentración. El exponente del coeficiente de difusión es -4

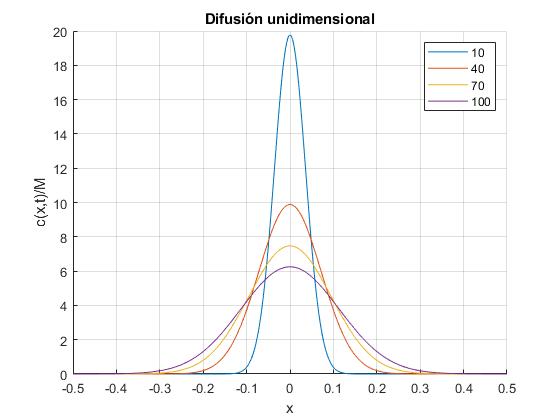
D=0.64e-4; %hidrógeno en aire
hold on
for t=10:30:100 %segundos
    f=@(x) exp(-x.^2/(4*D*t))/sqrt(4*D*t);
    fplot(f,[-0.5,0.5], 'displayName',num2str(t));
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('c(x,t)/M')
title('Difusión unidimensional')

Difusión de un soluto en el agua

El coeficiente de difusión de un soluto sólido en un disolvente, es sensible a la concentración, aunque supondremos disoluciones diluidas. Para bajas concentraciones, el coeficiente de difusión se mantiene aproximadamente constante. El exponente del coeficiente de difusión es -9

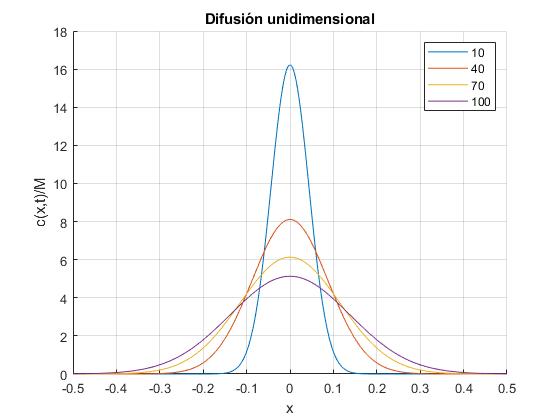
D=1.10e-9; %Sal común en agua
hold on
for t=(10:30:100)*24*3600 %horas_día*segundos cada hora
    f=@(x) exp(-x.^2/(4*D*t))/sqrt(4*D*t);
    fplot(f,[-0.5,0.5],'displayName',num2str(t/(24*3600)));
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('c(x,t)/M')
title('Difusión unidimensional')

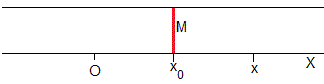
La masa M de soluto se distribuye inicialmente en un plano en la posición x₀. La concentración en en los puntos x del medio y en el instante t>0 es

${\displaystyle c(x,t)=\frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-x_0\right)}^2}{4Dt}\right)}$

Resultado que utilizaremos en el apartado 'Recinto de tamaño finito'

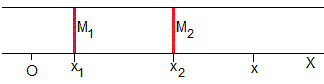
Situamos la masa M₁ de soluto en un plano en la posición x₁ y la masa M₂ de soluto en la posición x₂. Aplicando el principio de superposición, la concentración en en los puntos x del medio y en el instante t>0 es

${\displaystyle c(x,t)=\frac{M_1}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-x_1\right)}^2}{4Dt}\right)+\frac{M_2}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-x_2\right)}^2}{4Dt}\right)}$

Distribución inicial de masa extensa

En este apartado, estudiamos la difusión en un medio infinito en el que la la distribución inicial de masa ocupa una región.

La distribición inicial de masa ocupa una región semiinfinita

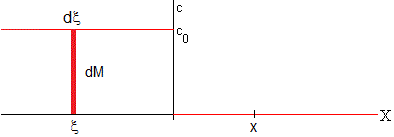
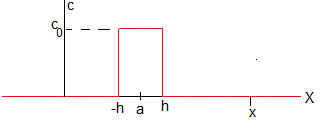
La concentración c(x,0) inicial en el instante t=0, es cero para x>0 y es constante c₀ para x≤0, tal como se muestra en la figura

La masa dM=c₀dξ está inicialmente distribuida en un plano situado en la posición ξ. La concentración en un punto x del medio y en el instante t es

${\displaystyle \frac{c_0·d\xi }{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-\xi \right)}^2}{4Dt}\right)}$

Aplicando el principio de superposición, sumamos la contribución a la concentración en la posición x y en el instante t de todas las masas dM distribuidas inicialmente en planos situados en las todas las posiciones ξ tal que -∞<ξ≤0

${\displaystyle c(x,t)={\displaystyle \underset{-\infty }{\overset{0}{\int }}\frac{c_0·d\xi }{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-\xi \right)}^2}{4Dt}\right)d\xi }}$

Haciendo el cambio de variable

${\displaystyle z=\frac{x-\xi }{\sqrt{4Dt}},dz=-\frac{d\xi }{\sqrt{4Dt}}}$

Obtenemos

${\displaystyle c(x,t)=-\frac{c_0}{\sqrt{\pi }}{\displaystyle \underset{\infty }{\overset{x/\sqrt{4Dt}}{\int }}\exp \left(-z^2\right)dz}=\frac{c_0}{\sqrt{\pi }}\left({\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-z^2\right)dz-{\displaystyle \underset{0}{\overset{x/\sqrt{4Dt}}{\int }}\exp \left(-z^2\right)dz}}\right)}$

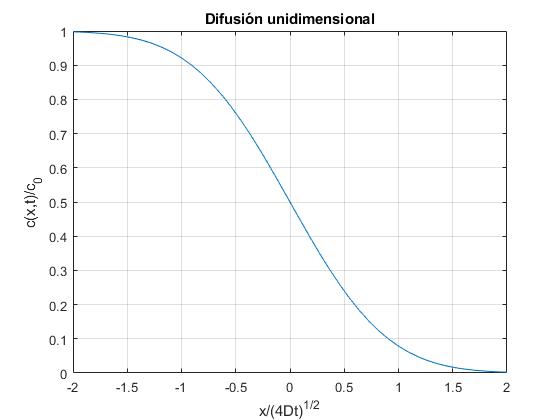
Expresamos las integrales en términos de la función error erf

${\displaystyle c(x,t)=\frac{c_0}{\sqrt{\pi }}\left(\frac{\sqrt{\pi }}{2}\text{-}\frac{\sqrt{\pi }}{2}\text{erf}\left(\frac{x}{\sqrt{4Dt}}\right)\right)=\frac{c_0}{2}\left(\text{1-erf}\left(\frac{x}{\sqrt{4Dt}}\right)\right)}$

f=@(x) (1-erf(x))/2;
fplot(f,[-2,2]);
grid on
xlabel('x/(4Dt)^{1/2}')
ylabel('c(x,t)/c_0')
title('Difusión unidimensional')

Difusión de la sal en el agua

El siguiente ejemplo, explica las características esenciales de la mezcla en un estuario, del agua salada procedente del mar con el agua de un río.  El agua del río menos densa fluye sobre el agua de mar. Hay por tanto, una discontinuidad en la densidad con la profundidad, debido a las diferencias de salinidad.

Consideremos la siguiente distribución unidimensional de la concentración en el instante t=0

c=c₀ para x≤0
c=0, para x>0

El coeficiente de difusión de la sal en agua pura es D=1.484·10^-9 m²/s

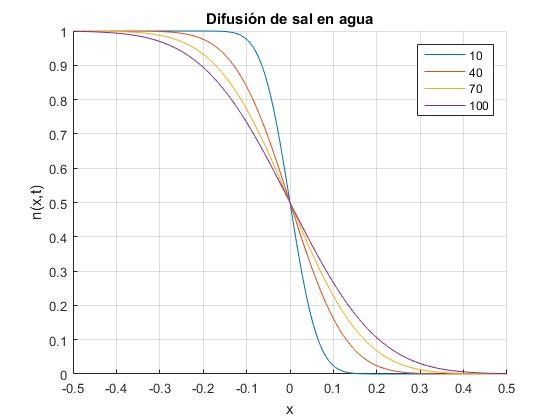
Se representa la concentración c(x, t)/c₀ de cada punto x del medio unidimensional en varios instantes.

D=1.484e-9; %Sal común en agua
hold on
for t=(10:30:100)*24*3600 %horas_día*segundos cada hora
    f=@(x) (1-erf(x/(2*sqrt(D*t))))/2;
    fplot(f,[-0.5,0.5], 'displayName',num2str(t/(24*3600)));
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('n(x,t)')
title('Difusión de sal en agua')

La distribición inicial de masa ocupa una región

Del mismo modo, estudiamos la difusión de una sustancia inicialmente confinada en la región (-h,h) centrada en el origen

${\displaystyle c(x,t)={\displaystyle \underset{-h}{\overset{h}{\int }}\frac{c_0·d\xi }{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-\xi \right)}^2}{4Dt}\right)d\xi }}$

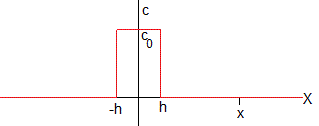
El resultado es

${\displaystyle \begin{array}{l}c(x,t)=-\frac{c_0}{\sqrt{\pi }}{\displaystyle \underset{(x+h)/\sqrt{4Dt}}{\overset{(x-h)/\sqrt{4Dt}}{\int }}\exp \left(-z^2\right)dz}=\frac{c_0}{\sqrt{\pi }}\left({\displaystyle \underset{0}{\overset{(x+h)/\sqrt{4Dt}}{\int }}\exp \left(-z^2\right)dz-{\displaystyle \underset{0}{\overset{(x-h)/\sqrt{4Dt}}{\int }}\exp \left(-z^2\right)dz}}\right)=\\ \frac{c_0}{\sqrt{\pi }}\left(\frac{\sqrt{\pi }}{2}\text{erf}\left(\frac{x+h}{\sqrt{4Dt}}\right)-\frac{\sqrt{\pi }}{2}\text{erf}\left(\frac{x-h}{\sqrt{4Dt}}\right)\right)=\frac{c_0}{2}\left(\text{erf}\left(\frac{x+h}{\sqrt{4Dt}}\right)-\text{erf}\left(\frac{x-h}{\sqrt{4Dt}}\right)\right)\end{array}}$

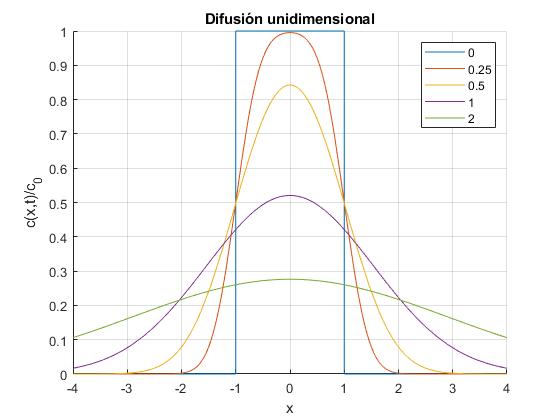
Representamos c(x,t)/c₀ para los instantes tales $\frac{\sqrt{Dt}}{h}=\mathrm{0,}\frac{1}{4},\frac{1}{2},\mathrm{1,}2$

hold on
for t=[0,1/4,1/2,1,2]
    f=@(x) (erf((x+1)/(2*t))-erf((x-1)/(2*t)))/2;
    fplot(f,[-4,4],'displayName',num2str(t))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('c(x,t)/c_0')
title('Difusión unidimensional')

Estudiamos la difusión de una sustancia inicialmente confinada en la región (-h,h) centrada en una posición a, resultado que utilizaremos en el apartado 'Recinto de tamaño finito'

${\displaystyle c(x,t)={\displaystyle \underset{a-h}{\overset{a+h}{\int }}\frac{c_0·d\xi }{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-\xi \right)}^2}{4Dt}\right)d\xi }}$

El resultado es

${\displaystyle \begin{array}{l}c(x,t)=-\frac{c_0}{\sqrt{\pi }}{\displaystyle \underset{(x-a+h)/\sqrt{4Dt}}{\overset{(x-a-h)/\sqrt{4Dt}}{\int }}\exp \left(-z^2\right)dz}=\frac{c_0}{\sqrt{\pi }}\left({\displaystyle \underset{0}{\overset{(x-a+h)/\sqrt{4Dt}}{\int }}\exp \left(-z^2\right)dz-{\displaystyle \underset{0}{\overset{(x-a-h)/\sqrt{4Dt}}{\int }}\exp \left(-z^2\right)dz}}\right)=\\ \frac{c_0}{\sqrt{\pi }}\left(\frac{\sqrt{\pi }}{2}\text{erf}\left(\frac{x-a+h}{\sqrt{4Dt}}\right)-\frac{\sqrt{\pi }}{2}\text{erf}\left(\frac{x-a-h}{\sqrt{4Dt}}\right)\right)=\frac{c_0}{2}\left(\text{erf}\left(\frac{x-a+h}{\sqrt{4Dt}}\right)-\text{erf}\left(\frac{x-a-h}{\sqrt{4Dt}}\right)\right)\end{array}}$

La evaporación como proceso de difusión

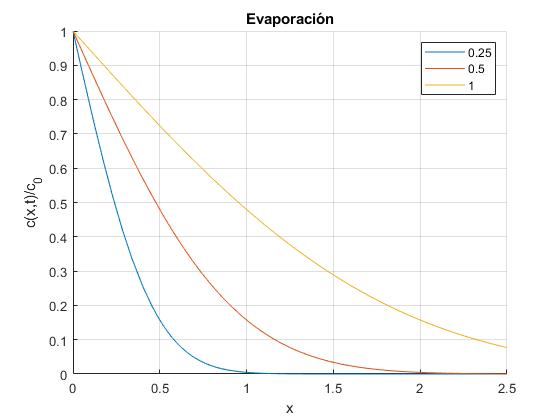
Supongamos que la concentración c₀ en x=0 se mantiene constante, la solución de la ecuación de la difusión es

${\displaystyle c(x,t)=c_0\left(1-\text{erf}\left(\frac{x}{\sqrt{4Dt}}\right)\right)}$

Encima de la superficie de un líquido a la temperatura T se crea una capa de vapor saturado en x=0, cuya concentración c_s se mantiene constante. Si encima de la superficie del líquido tenemos aire cuya concentración de vapor es c₀<c_s el vapor se difunde desde la capa límite hacia el aire. De este modo, el proceso de evaporación puede entenderse como un proceso de difusión. La solución de la ecuación de difusión es

${\displaystyle c(x,t)-c_0=\left(c_s-c_0\right)\left(1-\text{erf}\left(\frac{x}{\sqrt{4Dt}}\right)\right)}$

La extensión de la capa de vapor se va incrementando en proporción a la raiz cuadrada del tiempo t.

hold on
for t=[1/4,1/2,1] %producto Dt
    f=@(x) 1-erf(x/(2*t));
    fplot(f,[0,2.5],'displayName',num2str(t))
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('c(x,t)/c_0')
title('Evaporación')

Recinto de tamaño finito

Distribución inicial de masa en un plano

Hasta ahora hemos estudiado la difusión en un medio infinito o semiinfinito, supongamos un medio de extensión limitada 2L, desde (-L,L). Para resolver este problema se utiliza el principio de superposición y el método de las imágenes

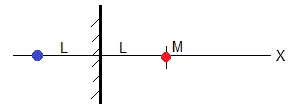
Supongamos que una masa M de soluto está distribuida en un plano situado en el origen x=0, en el instante t=0, la difusión tiene lugar en un recinto semiinfinito desde -L a ∞.

En la pared situada en x=-L no hay flujo de masa

${\displaystyle J\left(x=-L,t\right)=-D\frac{\partial c}{\partial x}=0}$

para que esto se cumpla, supondremos que una masa imagen M está distribuida en un plano situado en la posición x=-2L, en color azul. La pared actúa como un espejo

La concentración c(x,t) es la superposición

${\displaystyle c(x,t)=\frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{x^2}{4Dt}\right)+\frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x+2L\right)}^2}{4Dt}\right),t>0}$

Calculamos la derivada de la concentración c(x,t) con respecto a x

${\displaystyle \frac{\partial c(x,t)}{\partial x}=\frac{M}{\sqrt{4\pi Dt}}\left(\frac{-2x}{4Dt}\exp \left(-\frac{x^2}{4Dt}\right)-\frac{2\left(x+2L\right)}{4Dt}\exp \left(-\frac{{\left(x+2L\right)}^2}{4Dt}\right)\right)}$

Comprobamos que se anula para x=-L

Cuando el recinto se extiende desde (-L,L) los planos con las masas M inicialmente distribuidas son infinitas y sus posiciones se calculan tal como se muestra en la figura

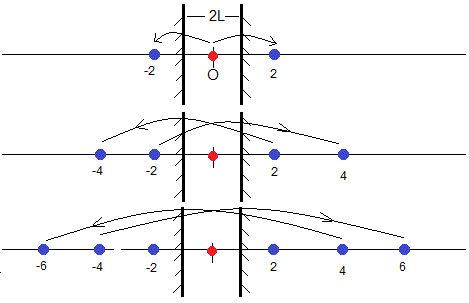
1. El plano con la masa M (color rojo) situado en el origen da lugar a dos planos imágenes (color azul) situadas en las posiciones -2L y 2L

2. El plano imagen situado en la posición -2L produce otra plano imagen situado en la posición 4L. El plano imagen situado en la posición 2L produce otro plano imagen situado en la posición -4L

3. El plano imagen situado en la posición -4L produce otro plano imagen situado en la posición 6L. El plano imagen situado en la posición 4L produce otro plano imagen situado en la posición -6L

4. ....

${\displaystyle \begin{array}{l}c(x,t)=\frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{x^2}{4Dt}\right)+\frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x+2L\right)}^2}{4Dt}\right)+\frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-2L\right)}^2}{4Dt}\right)+\\ \frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x+4L\right)}^2}{4Dt}\right)+\frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-4L\right)}^2}{4Dt}\right)+\\ \frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x+6L\right)}^2}{4Dt}\right)+\frac{M}{\sqrt{4\pi Dt}}\exp \left(-\frac{{\left(x-6L\right)}^2}{4Dt}\right)+\mathrm{...}\\ =\frac{M}{\sqrt{4\pi Dt}}{\displaystyle \sum _{n=-\infty }^{\infty }\exp \left(-\frac{{\left(x+2nL\right)}^2}{4Dt}\right)}\end{array}}$

Distribución inicial de masa extensa

La distribución inicial de masa puede ser extensa comprendida entre -h y h. En la figura se muestra la distribución inicial de masa en color rojo y sus imágenes en color azul

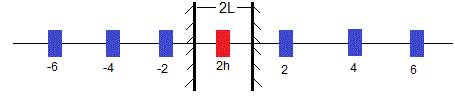
Los centros a de las distribiciones de masa están en las posiciones ...,-6L, -4L, -2L, 0, 2L, 4L, 6L, ...

${\displaystyle \begin{array}{l}c(x,t)=\frac{c_0}{2}\left(\text{erf}\left(\frac{x+h}{\sqrt{4Dt}}\right)-\text{erf}\left(\frac{x-h}{\sqrt{4Dt}}\right)\right)+\\ \frac{c_0}{2}\left(\text{erf}\left(\frac{x-2L+h}{\sqrt{4Dt}}\right)-\text{erf}\left(\frac{x-2L-h}{\sqrt{4Dt}}\right)\right)+\frac{c_0}{2}\left(\text{erf}\left(\frac{x+2L+h}{\sqrt{4Dt}}\right)-\text{erf}\left(\frac{x+2L-h}{\sqrt{4Dt}}\right)\right)\\ \frac{c_0}{2}\left(\text{erf}\left(\frac{x-4L+h}{\sqrt{4Dt}}\right)-\text{erf}\left(\frac{x-4L-h}{\sqrt{4Dt}}\right)\right)+\frac{c_0}{2}\left(\text{erf}\left(\frac{x+4L+h}{\sqrt{4Dt}}\right)-\text{erf}\left(\frac{x+4L-h}{\sqrt{4Dt}}\right)\right)+\mathrm{...}\\ c(x,t)=\frac{c_0}{2}{\displaystyle \sum _{n=-\infty }^{\infty }\left(\text{erf}\left(\frac{x-2nL+h}{\sqrt{4Dt}}\right)-\text{erf}\left(\frac{x-2nL-h}{\sqrt{4Dt}}\right)\right)}\end{array}}$

Estudimos la difusión de un soluto en una columna de agua

• La distribución inicial de masa está en un recinto comprendido entre -3 y 3 cm, h=0.03 m
• La difusión tiene lugar en una columna de agua de longitud 12 cm, L=0.06 m
• El coeficiente de difusión es, D=7.5·10^-10 m²/s
• Representamos c(x,t)/c₀ en los instantes 46, 109, 241, 1387, minutos

D=7.5e-10; %en agua
L=0.06; %recinto de tamaño 12 cm
h=0.03; %distribución de masa inicial en 6cm
hold on
x=linspace(-L,L,100);

for t=[46,109,241,1387]*60
    c=zeros(1,length(x));
    den=sqrt(4*D*t);
    for n=-10:10
       c=c+erf((x-2*n*L+h)/den)-erf((x-2*n*L-h)/den);
    end
    plot(x,c/2,'displayName',num2str(t/60));
end
hold off
grid on
legend('-DynamicLegend','location','northeast')
xlabel('x')
ylabel('c(x,t)')
title('Difusión unidimensional')

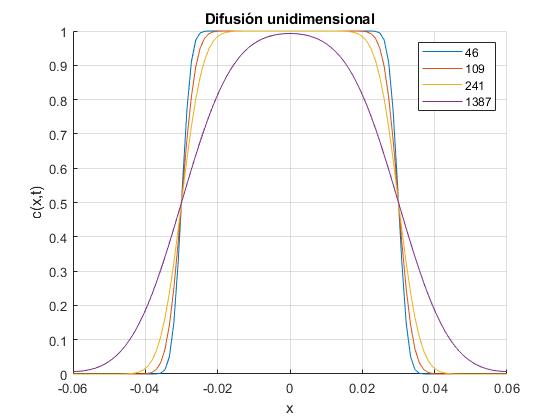
Se han tomado 21 términos del desarrollo en serie, pero bastan tres términos para obtener una buena aproximación

Variables separadas

Para resolver la ecuación diferencial en derivadas parciales

${\displaystyle \frac{1}{D}\frac{\partial c}{\partial t}=\frac{{\partial }^{2}c}{\partial x^2}}$

Buscamos una solución de la forma, c(x,t)=X(x)·T(t), denominada varables separadas

${\displaystyle \begin{array}{l}X\frac{dT}{dt}=DT\frac{d^{2}X}{d{x}^2}\\ \frac{1}{T}\frac{dT}{dt}=\frac{D}{X}\frac{d^{2}X}{d{x}^2}=-{\omega }^{2}D\end{array}}$

dado que la primera solamente depende de t y la segunda solamente depende de x. Transformamos una ecuación diferencial en derivadas parciales en un sistema de dos ecuaciones diferenciales cuyas soluciones son sencillas

${\displaystyle \{\begin{array}{l}\frac{1}{T}\frac{dT}{dt}=-{\omega }^{2}D\\ \frac{1}{X}\frac{d^{2}X}{d{x}^2}=-{\omega }^2\end{array}}$

La solución de la primera es

${\displaystyle T(t)=\exp \left(-{\omega }^{2}Dt\right)}$

La solución de la segunda es la de un Movimiento Armónico Simple

X(x)=Asin(ωx)+Bcos(ωx)

La solución completa es la superposición

${\displaystyle c(x,t)={\displaystyle \sum _{n=1}^{\infty }\left(A_n\sin \left({\omega }_{n}x\right)+B_n\cos \left({\omega }_{n}x\right)\right)}\exp \left(-{\omega }_n^{2}Dt\right)}$

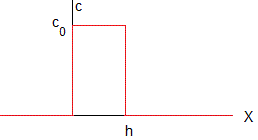
Las condiciones iniciales se muestran en la figura, la concentración es constante c₀ en el recinto de anchura h. c=c₀, para 0<x<h en el instante t=0

Las condiciones de contorno son: la concentración es nula, c(x,t)=0 para x=0 y x=h, t>0

• Las condiciones de contorno, determinan los posibles valores de ω.

X(x)=0, para x=0, implica que B=0
X(x)=0, para x=h, implica que sin(ωh)=0, ωh=nπ, n=1,2,3...

${\displaystyle {\omega }_n=\frac{n\pi }{h}}$

• Las condiciones iniciales determinan los coeficientes A_n

${\displaystyle \begin{array}{l}{c}_0={\displaystyle \sum _{m=1}^{\infty }{A}_m\sin \left(m\pi \frac{x}{h}\right)},0<x<h\\ c_0{\displaystyle \underset{0}{\overset{h}{\int }}\sin \left(n\pi \frac{x}{h}\right)dx}={\displaystyle \sum _{m=1}^{\infty }{A}_m{\displaystyle \underset{0}{\overset{h}{\int }}\sin \left(n\pi \frac{x}{h}\right)\sin \left(m\pi \frac{x}{h}\right)dx}},0<x<h\\ c_0\frac{h}{n\pi }\left(\cos (n\pi )-\cos 0\right)=A_n\frac{h}{2}\\ A_n=4\frac{c_0}{n\pi },n=\mathrm{1,3,5...}\end{array}}$

Para obtener este resultado hemos tenido en cuenta que

${\displaystyle {\displaystyle \underset{0}{\overset{h}{\int }}\sin \left(m\frac{x}{h}\right)}\sin \left(n\frac{x}{h}\right)dx=\{\begin{array}{l}\mathrm{0,}m\ne n\\ \frac{h}{2},m=n\end{array}}$

La solución es

${\displaystyle \begin{array}{l}c(x,t)=\frac{4c_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n}\sin \left(n\pi \frac{x}{h}\right)}\exp \left(-\frac{n^2}{h^2}{\pi }^{2}Dt\right)\\ c(x,t)=\frac{4c_0}{\pi }{\displaystyle \sum _{m=0}^{\infty }\frac{1}{2m+1}\sin \left((2m+1)\pi \frac{x}{h}\right)}\exp \left(-\frac{{\left(2m+1\right)}^2}{h^2}{\pi }^{2}Dt\right)\end{array}}$

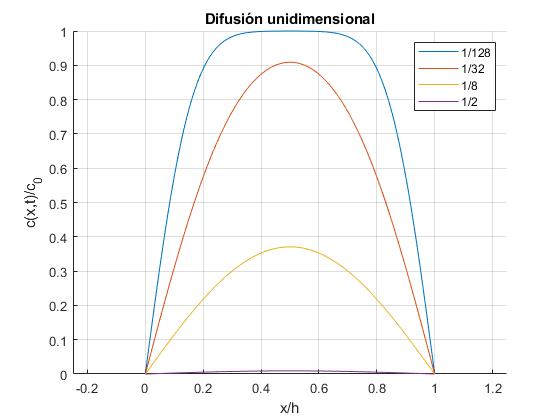
Representamos c(x,t)/c₀ en función de x/h en los instantes tal que Dt/h²=1/128, 1/32, 1/8, 1/2

hold on
x=linspace(0,1,100);
for t=[1/128, 1/32, 1/8, 1/2] %Dt/h^2
    c=zeros(1,length(x));
    for n=1:2:20
       c=c+sin(n*pi*x)*exp(-n^2*pi^2*t)*4/(n*pi);
    end
    plot(x,c);
end
hold off
xlim([-0.25,1.25])
grid on
legend('1/128', '1/32', '1/8', '1/2')
xlabel('x/h')
ylabel('c(x,t)/c_0')
title('Difusión unidimensional')

Difusión de una gota de tinta

Una gota de tinta de radio a se pone en un recipiente de agua de radio R, siendo a<<R. La profundidad del agua es pequeña, del orden de 1 cm, de modo que la gota de tinta alcanza el fondo del recipiente rápidamente y el movimiento de la tinta está determinado por el proceso de difusión únicamente.

El proceso de difusión bidimensional de la tinta en el agua se describe mediante la siguiente ecuación.

${\displaystyle \frac{{\partial }^{2}c}{\partial r^2}+\frac{1}{r}\frac{\partial c}{\partial r}=\frac{1}{D}\frac{\partial c}{\partial t}}$

donde D es el coeficiente de difusión de la tinta en agua y n es la concentración de tinta.

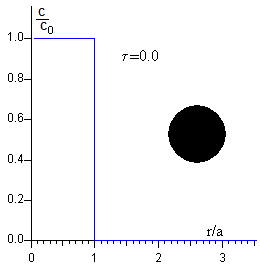
En el instante inicial t=0, la tinta está distribuida homogéneamente en el agua dentro de un círculo de radio a.

c=c₀ para r≤a
c=0 para r>a

La solución de la ecuación diferencial es (véase el tercer artículo citado en las referencias)

${\displaystyle c(r,t)=\frac{c_0}{2Dt}\exp \left(\frac{-r^2}{4Dt}\right){\displaystyle \underset{0}{\overset{a}{\int }}\exp }\left(\frac{-z^2}{4Dt}\right){\text{·I}}_{\text{0}}\left(\frac{r·z}{2Dt}\right)·z·dz}$

donde I₀(x) es la función modificada de Bessel de orden cero. Haciendo el cambio de variable

${\displaystyle x=\frac{r}{a}\zeta =\frac{z}{a}\tau =\frac{Dt}{a^2}}$

Obtenemos la ecuación

${\displaystyle \frac{c(x,\tau )}{c_0}=\frac{1}{2\tau }\exp \left(\frac{-x^2}{4\tau }\right){\displaystyle \underset{0}{\overset{1}{\int }}\exp }\left(\frac{-{\zeta }^2}{4\tau }\right)·{\text{I}}_{\text{0}}\left(\frac{x·\zeta }{2\tau }\right)·\zeta ·d\zeta }$

que es independiente del radio a de la gota y del coeficiente de difusión D de la tinta en el agua.

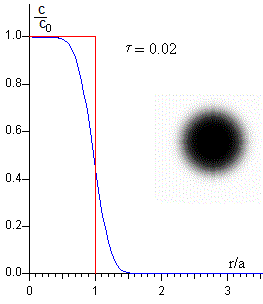
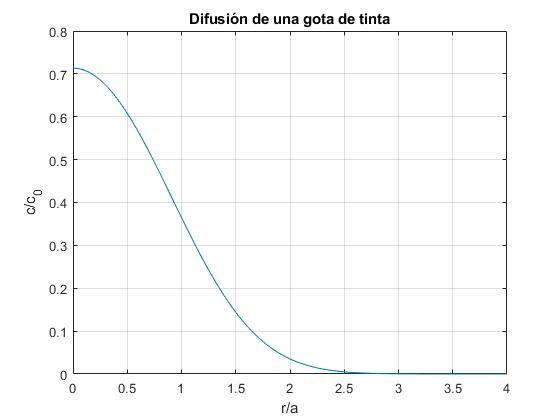
En la figura, se representa la concentración relativa c(x, τ)/c₀ en función de x=r/a (en color azul) y se compara con la situación inicial (color rojo) para el instante τ=0.02.

Conocido el valor del coeficiente de difusión D y el radio inicial de la gota a, determinamos la concentración c(r, t) de tinta a una distancia r=x·a del centro de la gota en el instante t=a²·τ/D

El programa es incapaz de calcular la concentración en función de la distancia x para un tiempo inferior a τ =0.003.

Como comprobación se puede verificar que

la cantidad total de tinta permanece constante, de modo que la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{c(x,\tau )}{c_0}2\pi ·x·dx}=\pi ·1^2·1=\pi }$

es proporcional a la cantidad inicial de tinta contenida en un círculo de radio unidad.

t=0.2;
x=0:0.02:4;
y=zeros(1,length(x));
for i=1:length(x)
    f=@(z) exp(-z.^2/(4*t)).*besseli(0, x(i)*z/(2*t)).*z;
    y(i)=integral(f,0,1)*exp(-x(i)^2/(4*t))/(2*t);
end
plot(x,y);
grid on
xlabel('r/a')
ylabel('c/c_0')
title('Difusión de una gota de tinta')

Actividades

Se introduce

• El tiempo τ en el control titulado Tiempo, un número mayor que 0.003.

Se pulsa el botón titulado Nuevo

A la derecha, se representa la concentración relativa c(x, τ)/c₀ en función de x=r/a (en color azul) y se compara con la situación inicial (color rojo). A la izquierda, se representa la concentración relativa en función de x codificada en una escala de grises.

Referencias

J Crank. The Mathematics of diffusion. Clarendon Press · Oxford (1975), pp. 11-18

Booth C., Beer T., Penrose J. Diffusion of salt in tap water. Am. J. Phys. 46 (5) May 1978. pp. 525-527.

Sanboh Lee, H-Y Lee, I-F Lee, C-Y Teeng. Ink diffusion in water. Eur. J. Phys. 25. (2004) pp. 331-336.

C. Graffney, Cheuk-Kin Chau. Using refractive index gradients to measure diffusivity between liquids. Am. J. Phys. 69 (7) July 2001, pp. 821-825