En una varilla metálica, el calor fluye desde las regiones donde la temperatura es más alta hacia las regiones en la que es más baja. La ley de Fourier establece que el flujo de calor J (energía por unidad de área y unidad de tiempo es proporcional al gradiente de temperatura.

${\displaystyle J=-K\frac{\partial T}{\partial x}}$

donde K se denomina conductividad térmica del material

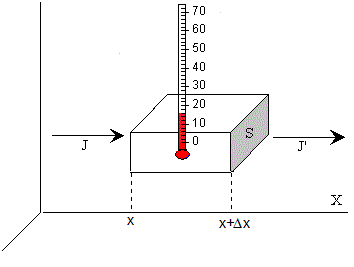
Sea una varilla de longitud L y área de la sección transversal S, con una distribución de temperatura no uniforme a lo largo del eje X, desde x=0 hasta x=L. La varilla está hecha de un material de densidad ρ, calor específico c y conductividad térmica K. Supongamos que las caras laterales de la varilla está aisladas y que no hay ninguna fuente de calor interna en la varilla.

Vamos a considerar un trozo de varilla de longitud Δx, entre x y x+Δx. En un intervalo de tiempo Δt, entra calor por su sección izquierda JSΔt y sale calor por su sección derecha J'SΔt. La diferencia se emplea en elevar la temperatura de dicho elemento de volumen que es el producto de la masa por el calor específico y por la diferencia de temperatura (final menos inicial), cρ(T(x,t+Δt)-T(x, t))

${\displaystyle \begin{array}{l}c\rho (S\Delta x)T(x,t+\Delta t)-c\rho (S\Delta x)T(x,t)=S\Delta t{\left(-K\frac{\partial T}{\partial x}\right)}_x-S\Delta t{\left(-K\frac{\partial T}{\partial x}\right)}_{x+\Delta x}\hfill \\ \frac{T(x,t+\Delta t)-T(x,t)}{\Delta t}=\frac{K}{c\rho }\frac{{\left(\frac{\partial T}{\partial x}\right)}_{x+\Delta x}-{\left(\frac{\partial T}{\partial x}\right)}_x}{\Delta x}\hfill \end{array}}$

En el límite cuando Δt→0 y Δx→0 obtenemos la ecuación que describe la conducción térmica.

${\displaystyle \frac{\partial T(x,t)}{\partial t}=\alpha \frac{{\partial }^{2}T(x,t)}{\partial x^2}}$

En general, la ecuación de la conducción del calor para un medio homogéneo, en el que la densidad ρ, calor específico c y conductividad térmica K es constante, se escribe

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}={\nabla }^{2}T}$

En coordenadas rectangulares T(x,y,z,t)

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\partial }^{2}T}{\partial z^2}}$

En coordenadas cilíndricas T(ρ,φ,z,t)

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial T}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}T}{\partial {\phi }^2}+\frac{{\partial }^{2}T}{\partial z^2}}$

En coordenadas esféricas, T(r,φ,θ,t)

${\displaystyle \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial T}{\partial r}\right)+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial r}\left(\sin \theta \frac{\partial T}{\partial \theta }\right)+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^{2}T}{\partial {\phi }^2}}$

Estudiaremos la conducción de calor unidimensional, a lo largo del eje X, o de la dirección radial en cuerpos que tengan simetría cilíndica o esférica.

${\displaystyle \begin{array}{l}\text{Rectangulares}\Rightarrow \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{{\partial }^{2}T}{\partial x^2}\\ \text{Cilíndricas}\Rightarrow \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial T}{\partial \rho }\right)\\ \text{Esféricas}\Rightarrow \frac{1}{\alpha }\frac{\partial T}{\partial t}=\frac{1}{r^2}\frac{\partial }{\partial r}\left(r^2\frac{\partial T}{\partial r}\right)\end{array}}$

Condición inicial

Para resolver esta ecuación hay que tener en cuenta la distribución inicial de temperaturas en el cuerpo T(x,0)

Condiciones de contorno

Supondremos que las caras laterales de la varilla está aisladas y solamente puede intercambiar calor con el exterior a través de sus extremos. Como ejemplos de condiciones de contorno citaremos los siguientes:

• Cuando la temperatura de los extremos de la varilla se mantienen fijos, por ejemplo, uno de los extremos intercambia calor con la atmósfera, por lo estará a la temperatura ambiente fija, y el otro extremo, está en contacto con un baño térmico que se mantiene una temperatura constante

• Alguno de los dos extremos está aislado y no puede intercambiar calor con el exterior

• Alguno de los dos extremos está conectado a una fuente de calor, suministrando un flujo de calor (energía por unidad de tiempo) constante

• Alguno de los dos extremos o ambos pierden calor por radiación. Vamos a estudiar este aspecto importante

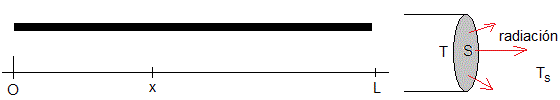
Supongamos una varilla metálica de longitud L, se ha calentado a una temperatura T₀, por el extremo x=L radia calor al ambiente cuya temperatura constante es T_s.

La energía emitida por un cuerpo negro a temperatura T por es proporcional a la cuarta potencia de la temperatura absoluta, T⁴ (Ley de Stefan). Por otra parte, el extremo de la barra absorbe radiación proveniente del ambiente, proporcional a la cuarta potencia de su temperatura absoluta. La cantidad de calor radiado dQ en el intervalo de tiempo dt, por una superficie de área S que está a la temperatura T es la diferencia

${\displaystyle \frac{dQ}{dt}=\sigma \left(T^4-T_s^4\right)S}$

Donde σ=5.67·10^-8 (Wm^-2K^-4) es la constante de Boltzmann

Este calor radiado proviene del interior de la varilla. En el mismo intervalo de tiempo dt, la cantidad de calor que llega a la superficie desde el interior de la varilla es

${\displaystyle -K\frac{\partial T}{\partial x}S·dt}$

donde K es la conductividad térmica del material. Igualando ambas cantidades

${\displaystyle \begin{array}{l}-K\frac{\partial T}{\partial x}=\sigma \left(T^4-T_s^4\right)=\sigma \left(T-T_s\right)\left(T+T_s\right)\left(T^2+T_s^2\right)\\ {\frac{\partial T(x,t)}{\partial x}|}_{x=L}\approx -h\left(T-T_s\right)h=\frac{4\sigma T_s^3}{K}\end{array}}$

Por ejemplo, para el aluminio la conductividad térmica K=209.3, a la temperatura ambiente T_s=293 K, obtenemos un valor de h=0.0273 m·K^-2

Hemos supuesto que la diferencia entre T y T_s es pequeña. Con esta aproximación, las pérdidas de calor son proporcionales a la diferencia de temperaturas (T-T_s) que es la ley del enfriamiento de Newton.

En general, cuando la diferencia de temperaturas entre un cuerpo y su medio ambiente no es demasiado grande, el calor transferido en la unidad de tiempo hacia el cuerpo o desde el cuerpo por conducción, convección y radiación es aproximadamente proporcional a la diferencia de temperatura entre el cuerpo y el medio externo.

${\displaystyle {-\frac{\partial T(x,t)}{\partial x}|}_{x=L}=h\left(T(L,t)-T_s\right)}$

Las condiciones de contorno en los problemas de condución del calor son los siguientes y sus combinaciones (por ejemplo una superficie que pierde calor y a la vez es iluminada por el sol):

• Temperaturas fijas en los extremos T(0,t)=T_a, T(L,t)=T_b

• Extremos aislados

${\displaystyle \begin{array}{l}{\frac{\partial T(x,t)}{\partial x}|}_{x=0}=0\\ {\frac{\partial T(x,t)}{\partial x}|}_{x=L}=0\end{array}}$

• Los extremos pierden calor. Ley del enfriamiento de Newton. T_s es la temperatura ambiente

${\displaystyle \begin{array}{l}{\frac{\partial T(x,t)}{\partial x}|}_{x=0}=h_1\left(T(\mathrm{0,}t)-T_s\right)\\ {-\frac{\partial T(x,t)}{\partial x}|}_{x=L}=h_2\left(T(L,t)-T_s\right)\end{array}}$

• Los extremos se ponen en contacto con una fuente de calor, q₀ o q_L (flujo de calor, energía por unidad de tiempo y área)

${\displaystyle \begin{array}{l}-{\frac{\partial T(x,t)}{\partial x}|}_{x=0}=\frac{q_0}{K}\\ {\frac{\partial T(x,t)}{\partial x}|}_{x=L}=\frac{q_L}{K}\end{array}}$

El estado estacionario

Se ha alcanzado el estado estacionario, cuando las temperaturas en los puntos de la barra no cambian con el tiempo. La temperatura es únicamente función de la posición x del punto.

• La ecuación del calor en coordenadas rectangulares es

${\displaystyle \frac{{\partial }^{2}T}{\partial x^2}=0}$

La solución de esta ecuación es T(x)=Ax+B. Donde A y B se determinan a partir de las condiciones de contorno. Por ejemplo, si el extremo x=0 de la barra está a una temperatura fija T_a y el extremo x=L está a una temperatura T_b

${\displaystyle T(x)=\frac{T_b-T_a}{L}x+T_a}$

• En coordenadas cilíndricas

${\displaystyle \frac{1}{\rho }\frac{d}{d\rho }\left(\rho \frac{dT}{d\rho }\right)=0}$

La solución es T(ρ)=Alnρ+B. Donde A y B se determinan a partir de las condiciones de contorno.

Supongamos un cilindro hueco, muy largo, de radio interior a y radio exterior b. En el interior, se genera un flujo de calor q y la superficie exterior está a la temperatura ambiente fija T_s

${\displaystyle \begin{array}{l}{-K\frac{\partial T(\rho ,t)}{\partial \rho }|}_{\rho =a}=q\\ T(b,t)=T_s\end{array}}$

La solución es

${\displaystyle T(\rho )=\frac{qa}{K}\ln \left(\frac{b}{\rho }\right)+T_s}$

• En coordendas esféricas

${\displaystyle \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dT}{dr}\right)=0}$

La solución es T(r)=A/r+B. Donde A y B se determinan a partir de las condiciones de contorno.

Supongamos una esfera hueca, de radio interior a y radio exterior b. En el interior, se genera un flujo de calor q y la superficie exterior está a la temperatura ambiente fija T_s

Las condiciones de contorno son idénticas a las del cilindro hueco del ejemplo anterior. La solución es

${\displaystyle T(r)=\frac{q{a}^2}{K}\left(\frac{1}{r}-\frac{1}{b}\right)+T_s}$

Fuente de calor

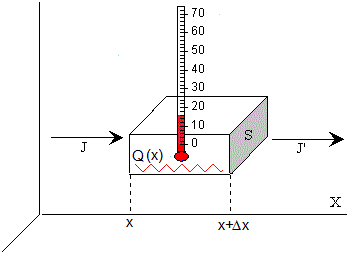
Sea una varilla de longitud L y área de la sección transversal S, con una distribución inicial de temperatura T(x,0) a lo largo del eje X, desde x=0 hasta x=L. La varilla está hecha de un material de densidad ρ, calor específico c y conductividad térmica K. Supongamos que las caras laterales de la varilla está aisladas y que se ha incorporado una fuente interna de calor Q(x), 0<x<L.

Vamos a considerar un trozo de varilla de longitud Δx, entre x y x+Δx. En un intervalo de tiempo Δt, entra calor por su sección izquierda JSΔt, sale calor por su sección derecha J'SΔt y además se genera calor Q(x) por unidad de volumen y en la unidad de tiempo. La diferencia se emplea en elevar la temperatura de dicho elemento de volumen que es el producto de la masa por el calor específico y por la diferencia de temperatura (final menos inicial), cρ(T(x,t+Δt)-T(x, t))

${\displaystyle \begin{array}{l}c\rho (S\Delta x)T(x,t+\Delta t)-c\rho (S\Delta x)T(x,t)=S\Delta t{\left(-K\frac{\partial T}{\partial x}\right)}_x-S\Delta t{\left(-K\frac{\partial T}{\partial x}\right)}_{x+\Delta x}+Q(x)S\Delta x\Delta t\\ \frac{T(x,t+\Delta t)-T(x,t)}{\Delta t}=\frac{K}{c\rho }\frac{{\left(\frac{\partial T}{\partial x}\right)}_{x+\Delta x}-{\left(\frac{\partial T}{\partial x}\right)}_x}{\Delta x}+\frac{Q(x)}{c\rho }\end{array}}$

En el límite cuando Δt→0 y Δx→0 obtenemos la ecuación que describe la conducción térmica con una fuente de calor en su interior.

${\displaystyle \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2}+\frac{Q}{\rho c}}$

Ejemplo: una esfera con una fuente de calor en su centro

Consideremos una esfera de radio R, con una fuente de calor en su centro. Supondremos que la esfera está en un ambiente cuya temperatura T_s no cambia

En el estado estacionario la ecuación de la conducción del calor se escribe

${\displaystyle \begin{array}{l}\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dT}{dr}\right)=-\frac{Q}{\alpha \rho c}\\ \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dT}{dr}\right)=-q\end{array}}$

Integramos dos veces con respecto a r, obteniendo

${\displaystyle T(r)=-q\frac{r^2}{6}+\frac{A}{r}+B}$

La constante A tiene que ser cero ya que T(r) para r=0 tiene que mantenerse finito. La constante B se determina a partir de la condición de contorno, T(R)=T_s

${\displaystyle T(r)=\frac{q}{6}\left(R^2-r^2\right)+T_s}$