La función error erf se define del siguiente modo:

${\displaystyle \text{erf}(x)=\frac{2}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{x}{\int }}\exp \left(-t^2\right)}dt}$

Llamamos a la función erf de MATLAB para representar gráficamente la función error.

fplot(@erf,[-2,2])
xlabel('x')
ylabel('erf(x)')
title('Función error')
grid on

Alternativamente

>> syms x;
>> ezplot(erf(x), [-2, 2])
>> grid on;

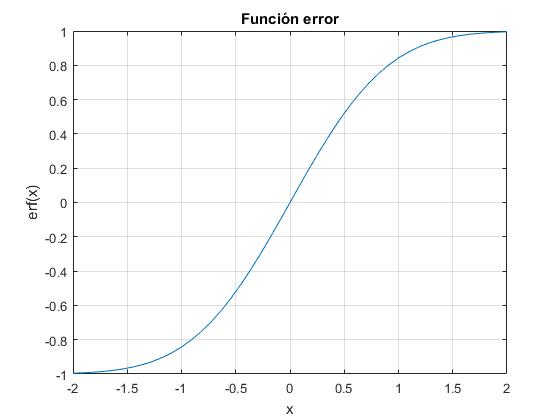
Esta función tiende asintóticamente a 1 cuando x se hace grande, ya que

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-t^2\right)}dt=\frac{\sqrt{\pi }}{2}}$

>> syms t;
>> y=exp(-t^2);
>> int(y,0,inf)
ans =pi^(1/2)/2

entonces, erf(∞)=1.

Fuerza descrita por una función de Gauss

Supongamos una partícula de masa m que se mueve a lo largo del eje X bajo la acción de una fuerza F(t) que depende del tiempo de la forma

${\displaystyle F(t)=F_0\exp \left(-\alpha {\left(t-t_0\right)}^2\right)0\le t\le 2t_0}$

Esta función tiende a cero cuando t→±∞ y presenta un máximo en t=t₀, cuya altura es F₀. α es un parámetro que controla la anchura del pico.

Una fuerza que actúa durante un tiempo 2t₀ produce un impulso.

${\displaystyle I={\displaystyle \underset{0}{\overset{2t_0}{\int }}F(t)·dt={\displaystyle \underset{0}{\overset{2t_0}{\int }}{F}_0\exp \left(-\alpha {\left(t-t_0\right)}^2\right)dt}}}$

Hacemos el cambio $u=\sqrt{\alpha }\left(t-t_0\right)$

${\displaystyle I=\frac{F_0}{\sqrt{\alpha }}{\displaystyle \underset{-\sqrt{\alpha }{t}_0}{\overset{\sqrt{\alpha }{t}_0}{\int }}\exp (-u^2)·du}=2\frac{F_0}{\sqrt{\alpha }}{\displaystyle \underset{0}{\overset{\sqrt{\alpha }{t}_0}{\int }}\exp (-u^2)·du}=F_0\sqrt{\frac{\pi }{\alpha }}\text{erf}\left(\sqrt{\alpha }{t}_0\right)}$

Expresamos la fuerza F(t) en términos del impulso I en vez del máximo F₀

${\displaystyle F(t)=I\sqrt{\frac{\alpha }{\pi }}\frac{\exp \left(-\alpha {\left(t-t_0\right)}^2\right)}{\text{erf}\left(\sqrt{\alpha }{t}_0\right)}0\le t\le 2t_0}$

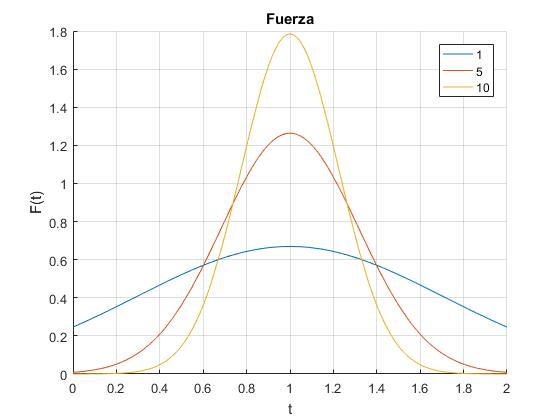
Representamos F(t) para tres valores del parámetro α: 1, 5, 10. El área bajo las curvas en el intervalo (0, 2t₀) es el impulso I cuyo valor es la unidad

t0=1; %posición del pico
I=1; %impulso
hold on
for alfa=[1,5,10] 
    F=@(t) I*sqrt(alfa/pi)*exp(-alfa*(t-t0).^2)/erf(sqrt(alfa)*t0);
    fplot(F,[0,2*t0],'displayName',num2str(alfa))
end
title('Fuerza')
xlabel('t')
ylabel('F(t)')
legend('-DynamicLegend','location','northeast')
grid on
hold off  

La aceleración a(t) es el cociente entre la fuerza F(t) y la masa m de la partícula. Integrando con respecto del tiempo, obtenemos la velocidad v(t). Supondremos que en el instante t=0, la partícula parte del reposo, v=0.

${\displaystyle \begin{array}{l}v(t)={\displaystyle \underset{0}{\overset{t}{\int }}\frac{F(t)}{m}dt}=\sqrt{\frac{\alpha }{\pi }}\frac{I}{m·\text{erf}\left(\sqrt{\alpha }{t}_0\right)}{\displaystyle \underset{0}{\overset{t}{\int }}\exp \left(-\alpha {\left(t-t_0\right)}^2\right)dt}=\\ \sqrt{\frac{1}{\pi }}\frac{I}{m·\text{erf}\left(\sqrt{\alpha }{t}_0\right)}{\displaystyle \underset{-\sqrt{\alpha }{t}_0}{\overset{\sqrt{\alpha }\left(t-t_0\right)}{\int }}\exp \left(-u^2\right)du}=\\ \sqrt{\frac{1}{\pi }}\frac{I}{m·\text{erf}\left(\sqrt{\alpha }{t}_0\right)}\left\{{\displaystyle \underset{-\sqrt{\alpha }{t}_0}{\overset{0}{\int }}\exp \left(-u^2\right)du}+{\displaystyle \underset{0}{\overset{\sqrt{\alpha }\left(t-t_0\right)}{\int }}\exp \left(-u^2\right)du}\right\}=\\ \sqrt{\frac{1}{\pi }}\frac{I}{m·\text{erf}\left(\sqrt{\alpha }{t}_0\right)}\left\{\frac{\sqrt{\pi }}{2}\text{erf}\left(\sqrt{\alpha }{t}_0\right)+\frac{\sqrt{\pi }}{2}\text{erf}\left(\sqrt{\alpha }\left(t-t_0\right)\right)\right\}=\\ \frac{I}{2m}\left\{1+\frac{\text{erf}\left(\sqrt{\alpha }\left(t-t_0\right)\right)}{\text{erf}\left(\sqrt{\alpha }{t}_0\right)}\right\}\end{array}}$

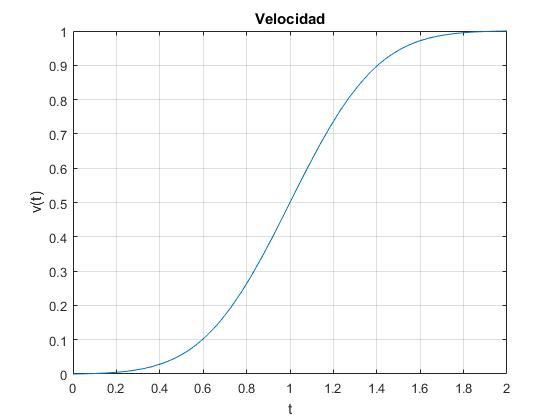
Representamos la velocidad en función del tiempo, para el valor del parámetro α=5

t0=1; %posición del pico
I=1; %impulso
alfa=5; %parámetro
v=@(t) (I/2)*(1+erf(sqrt(alfa)*(t-t0))/erf(sqrt(alfa)*t0));
fplot(v,[0,2*t0])
title('Velocidad')
xlabel('t')
ylabel('v(t)')
grid on

Dada la velocidad v(t) obtenemos la posición del móvil x(t) integrando respecto del tiempo. Supondremos que en el instante t=0, el cuerpo parte del origen, x=0.

Primero, integramos por partes la función error

${\displaystyle \begin{array}{l}{\displaystyle \int \text{erf}(x)·dx}\{\begin{array}{l}u=\text{erf}(x)\\ dv=dx\end{array}\{\begin{array}{l}du=\frac{2}{\sqrt{\pi }}\exp (-x^2)·dx\\ v=x\end{array}\\ {\displaystyle \int \text{erf}(x)·dx}=x·\text{erf}(x)-\frac{2}{\sqrt{\pi }}{\displaystyle \int x}·\exp (-x^2)·dx\\ {\displaystyle \int \text{erf}(x)·dx}=x·\text{erf}(x)+\frac{1}{\sqrt{\pi }}\exp (-x^2)+C\end{array}}$

>> syms x;
>> int(erf(x))
ans =exp(-x^2)/pi^(1/2) + x*erf(x)

Utilizamos este resultado para obtener la posición del móvil en función del tiempo

${\displaystyle \begin{array}{l}x(t)={\displaystyle \underset{0}{\overset{t}{\int }}v(t)·dt}=\frac{I}{2m}\left\{{\displaystyle \underset{0}{\overset{t}{\int }}dt}+\frac{1}{\text{erf}\left(\sqrt{\alpha }{t}_0\right)}{\displaystyle \underset{0}{\overset{t}{\int }}\text{erf}\left(\sqrt{\alpha }\left(t-t_0\right)\right)dt}\right\}=\\ \frac{I}{2m}\left\{t+\frac{1}{\sqrt{\alpha }}\frac{1}{\text{erf}\left(\sqrt{\alpha }{t}_0\right)}{\displaystyle \underset{-\sqrt{\alpha }{t}_0}{\overset{\sqrt{\alpha }\left(t-t_0\right)}{\int }}\text{erf}\left(u\right)dt}\right\}=\\ \frac{I}{2m}\left\{t+\frac{1}{\text{erf}\left(\sqrt{\alpha }{t}_0\right)}\left\{\left(t-t_0\right)\text{erf}\left(\sqrt{\alpha }\left(t-t_0\right)\right)+\frac{\exp \left(-\alpha {\left(t-t_0\right)}^2\right)}{\sqrt{\pi \alpha }}-t_0·\text{erf}\left(\sqrt{\alpha }{t}_0\right)-\frac{\exp \left(-\alpha t_0^2\right)}{\sqrt{\pi \alpha }}\right\}\right\}\end{array}}$

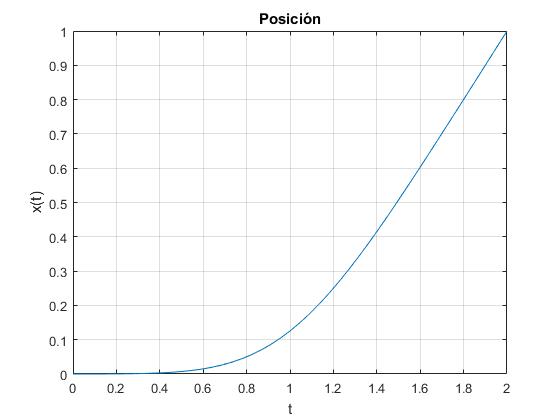
Representamos la posición del móvil en función del tiempo, para el valor del parámetro α=5

t0=1; %posición del pico
I=1; %impulso
alfa=5; %parámetro
x=@(t) (I/2)*(t+((t-t0).*erf(sqrt(alfa)*(t-t0))+exp(-alfa*(t-t0).^2)
/sqrt(pi*alfa)-t0*erf(sqrt(alfa)*t0)-exp(-alfa*t0^2)/sqrt(pi*alfa))
/erf(sqrt(alfa)*t0));
fplot(x,[0,2*t0])
title('Posición')
xlabel('t')
ylabel('x(t)')
grid on

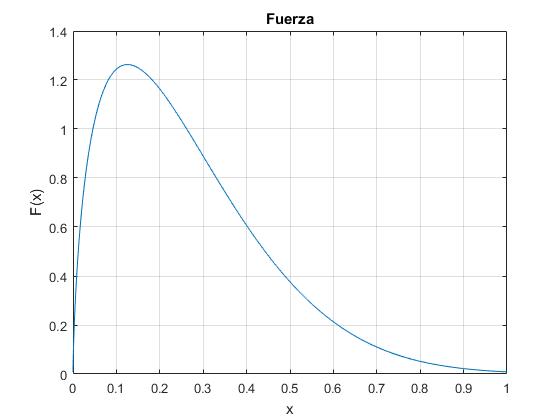
Representamos la fuerza F(x) en función de la posición del móvil, para el valor del parámetro α=5

t0=1; %posición del pico
I=1; %impulso
alfa=5; %parámetro
F=@(t) I*sqrt(alfa/pi)*exp(-alfa*(t-t0).^2)/erf(sqrt(alfa)*t0);
x=@(t) (I/2)*(t+((t-t0).*erf(sqrt(alfa)*(t-t0))+exp(-alfa*(t-t0).^2)
/sqrt(pi*alfa)-t0*erf(sqrt(alfa)*t0)-exp(-alfa*t0^2)/sqrt(pi*alfa))
/erf(sqrt(alfa)*t0));
t=linspace(0,2*t0,100);
plot(x(t),F(t))
title('Fuerza')
xlabel('x')
ylabel('F(x)')
grid on

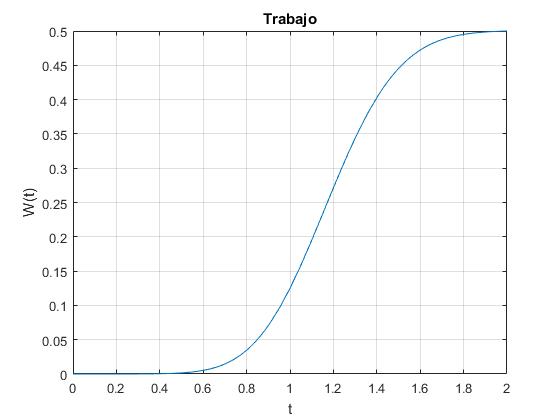
El trabajo realizado por la fuerza F(t) desde el instante t=0 al instante t, es igual a la energía cinética de la partícula que parte del reposo

${\displaystyle W(t)=\frac{1}{2}m{v}^2(t)}$

t0=1; %posición del pico
I=1; %impulso
alfa=5; %parámetro
v=@(t) (I/2)*(1+erf(sqrt(alfa)*(t-t0))/erf(sqrt(alfa)*t0));
W=@(t) v(t).^2/2;
fplot(W,[0,2*t0])
title('Trabajo')
xlabel('t')
ylabel('W(t)')
grid on

Referencias

S K Foong. Work done by a Gaussian impulse. Eur. J. Phys. 31 (2010) pp. 543-550

Ejemplos en el curso de Física

La ley de distribución de la energía entre las moléculas

Enfriamiento de un gas

Difusión de sal en agua