El principio de Arquímedes
Porción de fluido en equilibrio con el resto del fluido.
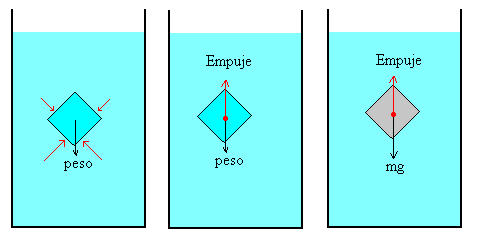
Consideremos, en primer lugar, las fuerzas sobre una porción de fluido en equilibrio con el resto de fluido. La fuerza que ejerce la presión del fluido sobre la superficie de separación es igual a p·dS, donde p solamente depende de la profundidad y dS es un elemento de superficie.
Puesto que la porción de fluido se encuentra en equilibrio, la resultante de las fuerzas debidas a la presión se debe anular con el peso de dicha porción de fluido. A esta resultante la denominamos empuje y su punto de aplicación es el centro de masa de la porción de fluido, denominado centro de empuje.
De este modo, para una porción de fluido en equilibrio con el resto, se cumple
Empuje=peso=ρf·gV
El peso de la porción de fluido es igual al producto de la densidad del fluido ρf por la aceleración de la gravedad g y por el volumen de dicha porción V.
Se sustituye la porción de fluido por un cuerpo sólido de la misma forma y dimensiones.
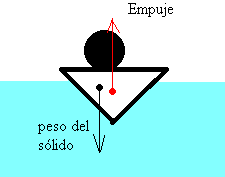
Si sustituimos la porción de fluido por un cuerpo sólido de la misma forma y dimensiones. Las fuerzas debidas a la presión no cambian, por tanto, su resultante que hemos denominado empuje es la misma y actúa en el mismo punto, denominado centro de empuje.
Lo que cambia es el peso del cuerpo sólido y su punto de aplicación que es el centro de masa, que puede o no coincidir con el centro de empuje.
Por tanto, sobre el cuerpo actúan dos fuerzas: el empuje y el peso del cuerpo, que no tienen en principio el mismo valor ni están aplicadas en el mismo punto.
En los casos más simples, supondremos que el sólido y el fluido son homogéneos y por tanto, coinciden el centro de masa del cuerpo con el centro de empuje.
Ejemplo 1
Supongamos un cuerpo sumergido de densidad ρ rodeado por un fluido de densidad ρf. El área de la base del cuerpo es A y su altura h.
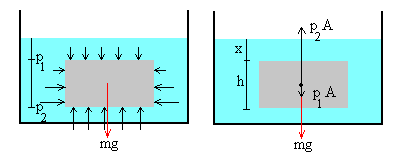
La presión debida al fluido sobre la base superior es p1=ρfgx, y la presión debida al fluido en la base inferior es p2=ρfg(x+h). La presión sobre la superficie lateral es variable y depende de la altura, está comprendida entre p1 y p2.
Las fuerzas debidas a la presión del fluido sobre la superficie lateral se anulan. Las otras fuerzas sobre el cuerpo son las siguientes:
-
Peso del cuerpo, mg
-
Fuerza debida a la presión sobre la base superior, p1·A
-
Fuerza debida a la presión sobre la base inferior, p2·A
En el equilibrio tendremos que
mg+p1·A=
p2·A
mg+ρfgx·A= ρfg(x+h)·A
o bien,
mg=ρfh·Ag
Como la presión en la cara inferior del cuerpo p2 es mayor que la presión en la cara superior p1, la diferencia es ρfgh. El resultado es una fuerza hacia arriba ρfgh·A sobre el cuerpo debida al fluido que le rodea.
Como vemos, la fuerza de empuje tiene su origen en la diferencia de presión entre la parte superior y la parte inferior del cuerpo sumergido en el fluido.
Excepciones
Con esta explicación surge un problema interesante y debatido. Supongamos que un cuerpo de base plana (cilíndrico o en forma de paralepípedo) cuya densidad es mayor que la del fluido, descansa en el fondo del recipiente.
Si no hay fluido entre el cuerpo y el fondo del recipiente ¿desaparece la fuerza de empuje?

En la figura, se representa la resultante Fp de las fuerzas debidas a la presión del fluido sobre el cuerpo sumergido. En la figura de la izquierda
Fp=(p0+ρg(H-h))A
Siendo A el área de la base del cuerpo de altura h, H es la altura del líquido en el recipiente, y p0 la presión atmosférica
Fp=pbA-ρVg
Siendo pb=p0+ρgH, la presión en el fondo del recipiente y V el volumen del cuerpo
Si se llena un recipiente con agua y se coloca un cuerpo en el fondo, el cuerpo quedaría en reposo sujeto por su propio peso mg y la fuerza Fp que ejercería la columna de fluido situada por encima del cuerpo, incluso si la densidad del cuerpo fuese menor que la del fluido.
Experiencia
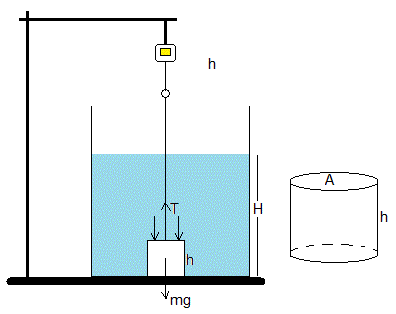
En un recipiente grande, situamos boca abajo un cilindro de sección A y altura h abierto por arriba. Al llenar el recipiente con líquido de densidad ρ, nos aseguramos de que no penetra en el cilindro a lo largo de su borde inferior en contacto con la base del recipiente. Dentro del cilindro solamente habrá aire a la presión atmosférica.
Atamos el cilindro a un sensor de fuerza, para medir la tensión T necesaria para levantar el cilindro.
Esta tensión T será la suma del peso del cilindro, mg, y de la fuerza que ejerce la presión del líquido por encima del cilindro, ρg(H-h)A
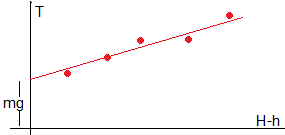
La tensión T se incrementa linealmente con la altura de líquido H-h por encima del cilindro
Ejemplo 2
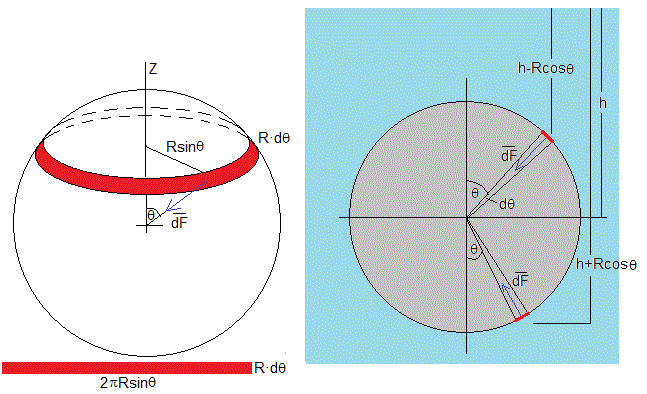
Consideremos una cuerpo de forma esférica de radio R, completamente sumergido en un líquido de densidad ρf. El centro de la esfera está a una profundidad h>R.
La presión que ejerce el líquido a una profundidad h-Rcosθ es p=ρf·g(h-Rcosθ), la fuerza que ejerce esta presión sobre el área dA señalada en color rojo es dF=p(2πRsinθ·R·dθ) y su dirección es radial y hacia el centro de la esfera
La presión que ejerce el líquido a una profundidad h+Rcosθ es p=ρf·g(h+Rcosθ), la fuerza que ejerce esta presión sobre el área dA es dF=p(2πRsinθ·R·dθ) y su dirección es radial y hacia el centro de la esfera
Su componente a lo largo del eje vertical Z es dF·cosθ
Su componente a lo largo del eje vertical Z es dF·cosθ
Por simetría las componentes horizontales se anulan
La fuerza total que ejerce la presión del fluido sobre la superficie de la esfera es hacia arriba e igual a la diferencia
Verificamos de nuevo, el principio de Arquímedes, el empuje es igual al producto de la densidad del fluido, la gravedad y el volumen del cuerpo sumergido
Flotación entre dos líquidos no miscibles
Un cuerpo sólido está sumergido en dos líquidos inmiscibles: agua y aceite. Determinaremos la densidad de dicho cuerpo por dos métodos distintos:
- El principio de Arquímedes
- La ecuación fundamental de la estática de fluidos
El aceite que tiene una densidad 0.8 g/cm3 se sitúa en la parte superior y el agua que es más densa 1.0 g/cm3 se sitúa en la parte inferior del recipiente.
La densidad del bloque es un número comprendido entre la densidad del aceite 0.8, y la del agua 1.0. Un cuerpo de esta densidad flota entre los dos líquidos.
Principio de Arquímedes
Conociendo que parte del sólido está sumergido en aceite (fluido 1) o en agua (fluido 2), se determinará la densidad de dicho cuerpo.
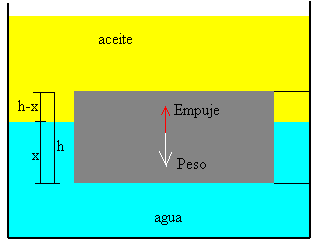
El principio de Arquímedes nos dice que si el bloque está en equilibrio, el peso del bloque debe ser igual al empuje proporcionado por ambos líquidos.
Peso del bloque =empuje del agua + empuje del aceite
ρShg=ρ2Sxg+ρ1S(h-x)g
S es el área de la base del bloque, h su altura, y x es la parte del bloque sumergida en agua.
En general, un cuerpo que flota en la superficie del agua, está sumergido en dos fluidos, uno es el agua ρ2=1000 kg/m3 y el otro es el aire ρ1=1.29 kg/m3. Habitualmente, se desprecia la densidad del aire frente a la del sólido ρ y la del fluido ρ2, aplicándose la fórmula aproximada
Ejemplo
Supongamos un bloque de h=20 cm de altura, observamos que el bloque está sumergido 13 cm en aceite y 7 cm en agua.
ρ·20=0.8·13+1.0·7
Despejando en la fórmula la densidad del sólido, obtenemos el valor de 0.87 g/cm3.
Ecuación fundamental de la estática de fluidos
Sean p1 y p2 las presiones sobre la cara superior e inferior del bloque sumergido.
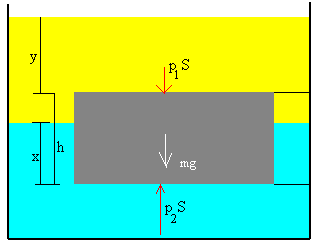
La cara superior está en el aceite a una profundidad y. La presión p1 será igual a la atmosférica p0 más la correspondiente a la altura y de aceite.
p1=p0+ρ1gy
La cara inferior está en el agua. La presión p2 será igual a la presión atmosférica p0 más la correspondiente a la altura de aceite (y+h-x) más la correspondiente a la altura de la columna de agua (x)
p2=p0+ρ1g(y+h-x)+ρ2gx
La fuerza que ejerce el fluido sobre dichas caras será el producto de la presión por el área de su superficie S.
Como vemos en la figura, para que haya equilibrio se tiene que cumplir que
p1S+mg=p2S
Teniendo en cuenta que m=ρ·hS despejamos el valor de x.
Es el mismo resultado que hemos obtenido aplicando el principio de Arquímedes
Ejemplo:
Datos: densidad del agua 1000 kg/m3, densidad del aceite 800 kg/m3, densidad del mercurio 13550 kg/m3
La cara superior está a 22 cm de la superficie libre, la presión debida al aceite es
La cara inferior está a 42 cm de la superficie libre (35 cm de aceite y 7 cm de agua), la presión debida a ambos líquidos es:
En el equilibrio se cumple
Se obtiene ρs=870 kg/m3 ó 0.87 g/cm3
El principio de Arquímedes en un fluido en rotación
En un fluido de densidad ρf en equilibrio, la presión crece linealmente con la profundidad h, p=p0+ρfgh. p0 es la presión en la superficie del fluido
Un cuerpo sumergido experimenta una fuerza de empuje hacia arriba, E=ρfgV
-
La fuerza total sobre el cuerpo sumergido es el empuje E menos el peso mg,
Por otra parte,
En un fluido en rotación con velocidad angular constante ω, la presión crece proporcionalmente al cuadrado de la distancia al eje de rotación,
Un cuerpo sumergido experimenta una fuerza de empuje en la dirección radial, hacia el eje de rotación E=ρf(ω2r0)V.
La fuerza total sobre el cuerpo sumergido es la fuerza centrífuga menos el empuje en la dirección radial,
En este apartado, vamos a calcular la fuerza de empuje que experimenta una esfera de radio R sumergida en un fluido de densidad ρf en rotación con velocidad angular constante ω, el centro de la esfera está a una distancia r0=h del eje de rotación paralelo al eje Y
Vamos a seguir los mismos pasos que en el ejemplo de una esfera sumergida en un fluido en equilibrio
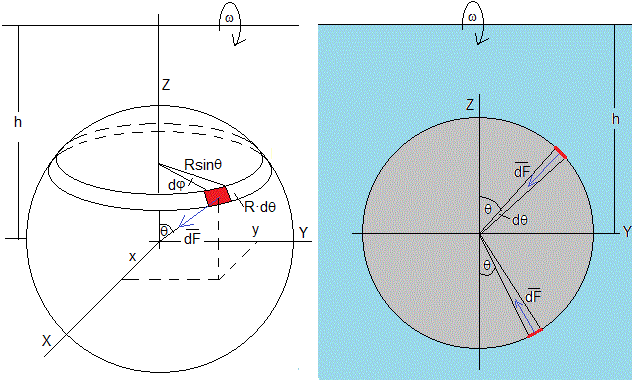
Presión en un punto z>0
Sea un punto P sobre la superficie esférica de radio R, de coordenadas φ, θ
La distancia del punto P al eje de rotación, la recta z=h, paralela al eje Y se calcula del siguiente modo
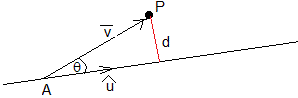
Tomamos un punto A de la recta y un vector unitario cuya dirección es la de la recta. El vector tiene origen en el punto A de la recta y extremo en el punto P.
El módulo del producto vectorial de los dos vectores es la distancia d del punto P a la recta.
Tomamos como punto A (0,0,h), el vector unitario , tiene la dirección de la recta paralela al eje Y. El vector va del punto A al punto P, es el vector
El producto vectorial
El módulo del producto vectorial es la distancia r=d del punto P al eje de rotación, la recta z=h, paralela al eje Y
La fuerza que ejerce dicha presión sobre el elemento diferencial de área (Rsinθ·dθ)·(R·dφ), señalado de color rojo en la figura, es dF=p(r)·(R2sinθ· dθ·dφ), tiene dirección radial y sentido hacia el centro de la esfera, tal como se indica en la figura.
La componente a lo largo del eje Z de dicha fuerza es dF·cosθ
Presión en otro punto z<0
Cuando el punto P, está por debajo del origen O, el vector es
La distancia r entre el eje de rotación y el punto P es
La fuerza que ejerce dicha presión sobre el elemento diferencial de área es dF=p(r)·(R2sinθ· dθ·dφ), tiene dirección radial y sentido hacia el centro de la esfera, (véase la figura de la derecha)
La componente a lo largo del eje Z de dicha fuerza es dF·cosθ
Empuje
La diferencia entre las dos fuerzas
Integramos el ángulo φ entre 0 y 2π y el ángulo θ entre 0 y π/2
Por simetría, las componentes de las fuerzas que ejerce la presión a lo largo del eje X e Y se anulan de dos en dos. La fuerza neta que ejerce la presión, debida a la rotación del fluido, sobre una esfera de radio R, sumergida en dicho fluido cuyo centro está a una distancia h del eje de rotación, tiene dirección radial sentido hacia el eje y vale ρf(ω2h)V. La aceleración de la gravedad g ha sido substituida por la aceleración centrífuga, ω2h.
Referencias
Bierman J, Kincanon E. Reconsidering Archimedes’ principle. The Physics Teacher, Vol 41, September 2003, pp. 340-344.
Gerald L. Wick, Paul F. Tooby. Centrifugal buoyancy forces Am. J. Phys. 45 (11), November 1977, pp. 1074-1076
Armand Le Noxaïc, Clémence Alglave. Is There a Buoyant Force That Acts on a Submerged Object with No Liquid Under It?. The Physics Teacher, Vol. 62, November 2024, pp. 682-683

