Modelo del interior de la Tierra.
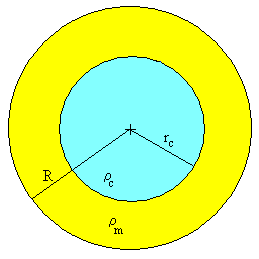
La variación de la densidad de la Tierra con el radio es bien conocida actualmente (véase el artículo citado en las referencias). La densidad aumenta al disminuir el radio, experimentando un cambio brusco para rc=3490 km o rc/R=0.548. El interior de la Tierra se divide en dos partes: el núcleo una esfera de radio rc y el manto, una capa esférica de radio interior rc y exterior R.
Una de las consecuencias más sorprendentes es que, la aceleración de la gravedad aumenta con la profundidad hasta alcanzar un máximo y luego, disminuye.
 |
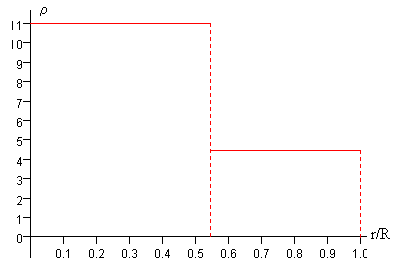 |
Vamos a estudiar un modelo de Tierra que consta de un núcleo de radio rc=3490 km y densidad constante ρc=11.0 g/cm3 y un manto de radio interior rc y radio exterior R=6371 km de densidad constante ρm=4.437 g/cm3.
Naturalmente, ρc, ρm y la densidad media ρ=5.517 g/cm3 están relacionadas mediante la ecuación
Variación de la aceleración de la gravedad g con el radio r
En la página titulada “Aceleración de la gravedad” demostramos que la aceleración de la gravedad g en un punto P en el interior de una distribución esférica de masa, se debe solamente a la masa contenida en la esfera de radio r<R, y se calcula mediante la fórmula
-
La aceleración de la gravedad en un punto situado en el interior del núcleo r<rc
g=19.577 (r/R) m/s2
-
La aceleración de la gravedad en un punto situado en el interior del manto rc<r<R
g=1.920(R/r)2+7.898(r/R) m/s2
-
La aceleración de la gravedad en un punto situado en el exterior de la Tierra r>R
g=9.82(R/r)2 m/s2
tal como hemos calculado en la página titulada "Aceleración de la gravedad"
En la figura, se muestra la dependencia del módulo de g con el cociente r/R (en color rojo) y se compara con el valor de g en función de (r/R) suponiendo la Tierra homogénea (en color azul), de densidad constante e igual a la densidad media
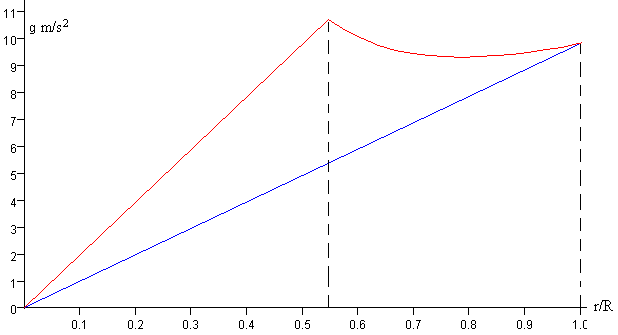
La aceleración de la gravedad crece linealmente con el radio r, en el núcleo para r<rc. En el manto g varía relativamente poco, disminuyendo al principio y aumentando al final, tal como vemos con más detalle en la figura inferior.
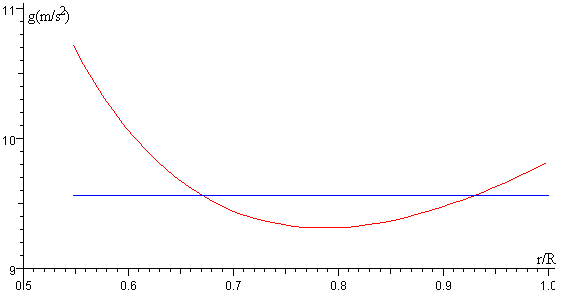
Calculamos el valor mínimo de la aceleración de la gravedad en el manto, derivando g con respecto de r e igualando a cero.
En una primera aproximación, podemos tomar la aceleración de la gravedad en el manto como constante e igual al siguiente valor medio (recta de color azul).
Energía potencial
Una partícula de masa m experimenta una fuerza F=mg dirigida radialmente hacia el centro de la Tierra. La energía potencial Ep(r) correspondiente a esta fuerza conservativa se calcula del siguiente modo
Tomamos como nivel cero de energía potencial Ep(∞)=0
-
Energía potencial de la partícula para r>R
Para r>R, la expresión de la fuerza sobre la partícula es
La expresión de la energía potencial en este intervalo es
-
Energía potencial de la partícula para rc<r<R
La expresión de la fuerza sobre la partícula en esta región es
La expresión de la energía potencial en este intervalo es
Para obtener esta expresión, se ha empleado la relación entre las densidades del manto ρm, núcleo ρc y media ρ.
-
Energía potencial de la partícula para 0<r<rc
La expresión de la fuerza sobre la partícula en esta región es
La expresión de la energía potencial en este intervalo es
En la figura, se representa la energía potencial Ep(r) (en color rojo) en función del cociente (r/R), y se compara con la energía potencial correspondiente al modelo de Tierra homogénea (en color azul).
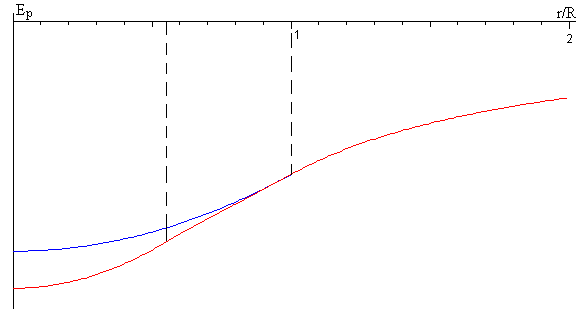
El principio de conservación de la energía
Conocida la posición r0 inicial y la velocidad inicial v0 de la partícula, calculamos la velocidad v de la partícula para una determinada posición r.
Para un determinado valor de la energía total, una partícula que atraviese la Tierra a través de uno de sus diámetros alcanzará una velocidad mayor, para una determinada distancia al centro, en el modelo de dos capas, que en el modelo de Tierra homogénea.
Presión en el centro de la Tierra
La ecuación fundamental de la hidrostática es
En la página titulada "La aceleración de la gravedad" calculamos la presión en el centro de la Tierra suponiendo que la densidad de la Tierra es constante e igual a la densidad media. La presión en el modelo más realista de núcleo más manto ambos de densidad constante es
donde p0=1.013·105 Pa es la presión para r=R es decir, la presión atmosférica, que es despreciable frente a la presión creada en el centro por el manto y el núcleo.
p=3.29·1011 Pa
Aproximación
Si consideramos la aceleración de la gravedad constante en el manto e igual a su valor medio gm. La expresión para la presión p en el centro de la Tierra es mucho más simple.
p=3.28·1011 Pa
Momento de inercia
El momento de inercia es un parámetro muy importante en el estudio del movimiento de la Tierra.
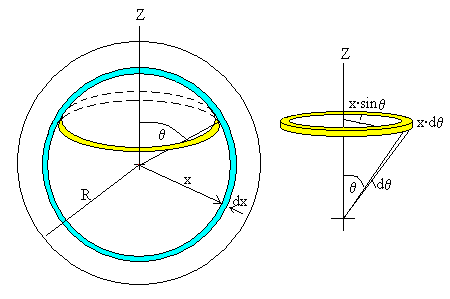
Consideramos la distribución esférica de masa M y radio R, dividida en capas esféricas de radio x y de espesor dx. Cada capa esférica a su vez, la dividimos en anillos de radio variable x·senθ. La masa contenida en el anillo es dm=ρ·(2πxsenθ)·(x·dθ)·dx.
El momento de inercia del anillo respecto del eje de rotación Z es
(xsenθ)2·dm
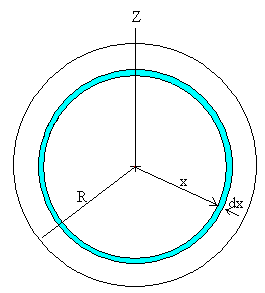 |
Integramos con respecto del ángulo θ para calcular el momento de inercia de la capa esférica de radio x y de espesor dx, respecto del eje de rotación Z.
|
El momento de inercia del núcleo con respeto al eje Z es
El momento de inercia del manto respecto del eje Z es
El momento de inercia de la Tierra respecto del eje Z es
I=Ic+Im=9.543·1036+7.412·1037=8.366·1037 kgm2=0.345·MR2
Siendo M=5.98·1024 kg la masa de la Tierra, y R=6.371·106 m el radio de la Tierra
El momento de inercia de una distribución esférica y homogénea de masa es I=2MR2/5=0.40MR2
Túnel que atraviesa la Tierra por un diámetro
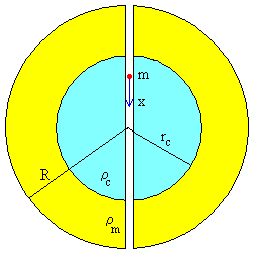 |
Se construye un túnel que atraviesa la Tierra por uno de sus diámetros. Vamos a estudiar el movimiento de una partícula de masa m que se suelta en un extremo del túnel. Calcularemos el tiempo que tarda en completar una oscilación. |
La fuerza que ejerce la Tierra sobre una partícula de masa m es mg, dirigida radialmente hacia el centro de la Tierra, su aceleración es g.
-
La ecuación del movimiento de la partícula cuando se encuentra en el manto rc<x<R es
La partícula parte de la posición x=R con velocidad nula dx/dt=0, llega al núcleo, x=rc en el instante tm con velocidad -vm.
Para calcular vm aplicamos el principio de conservación de la energía. La partícula parte del reposo desde un punto que dista r=R del centro de la Tierra y llega a un punto en el interior del manto que dista r centro de la Tierra, con velocidad v.
Cuando llega al límite entre el manto y el núcleo, r=rc,
Para llegar a esta expresión se ha empleado la relación entre las densidades del manto ρm, núcleo ρc y media ρ.
Con los datos:
G=6.67·10-11 N·m2/kg2,
Densidad del núcleo ρc=11000 kg/m3,
Densidad del manto ρm=4437 kg/m3,
Radio del núcleo rc=3.490·106 m
Radio de la Tierra R=6.371·106 m
Se obtiene vm=7444.3 m/s
Para obtener el tiempo tm, resolvemos la ecuación diferencial de segundo orden por procedimientos numéricos
-
La ecuación del movimiento en el núcleo es
En el núcleo la partícula describe un MAS cuya frecuencia angular es
ω=0.00175 rad/s
La solución de la ecuación diferencial del movimiento es
x=Asin(ωt)+Bcos(ωt)
dx/dt=Aωcos(ωt)-Bωsin(ωt)Los coeficientes A y B se determina a partir de las condiciones iniciales
Ponemos el contador de tiempo parcial a cero t=0, x=rc, dx/dt=-vm.
El tiempo que tarda en llegar al centro de la Tierra x=0 es
La velocidad que alcanza al llegar al centro de la Tierra es
Para obtener la expresión anterior se ha empleado las relaciones trigonométricas
Obtenemos esta velocidad aplicando el principio de conservación de la energía. La partícula parte del reposo desde un punto que dista r=R del centro de la Tierra y llega a un punto en el interior del núcleo que dista r centro de la Tierra, con velocidad v.
La velocidad cuando pasa por el centro de la Tierra, para r=0 es
Con los datos del modelo de Tierra: tc=392.4 s, v=9635.9 m/s, que en el modelo de Tierra homogénea da el valor v=7913.0 m/s
Completamos un cuarto de oscilación en el tiempo tm+tc. El periodo de unas oscilación es P=4(tc+tm)
Aproximación para el movimiento de la partícula en el manto
Se describe de forma aproximada el movimiento de la partícula, suponiendo que la aceleración de la gravedad en el manto es constante e igual al valor medio gm.
En el manto el movimiento de la partícula es rectilíneo uniformemente acelerado
Llega al núcleo x=rc en el instante tm con velocidad -vm.
Sabiendo que la aceleración de la gravedad media en el manto es gm=9.57 m/s2, la velocidad de la partícula cuando alcanza el núcleo es vm=7424.5 m/s, un valor próximo al calculado mediante el principio de conservación de la energía o resolviendo la ecuación diferencial del movimiento por procedimientos numéricos.
-
El tiempo que tarda en llegar al núcleo desde que se suelta en el extremo del túnel es tm=775.9 s
-
El tiempo que tarda en llegar al origen a través del núcleo es tc=393.2 s
A partir de aquí, la partícula describe un MAS, hasta que llega a la frontera entre el núcleo y el manto x=-rc, con velocidad –vm. En el manto se frena la partícula hasta que llega a x=-R en reposo, completando medio ciclo de oscilación. El periodo P=4(tc+tm)=4676.4 s=77.9 min
Túnel a lo largo de una cuerda
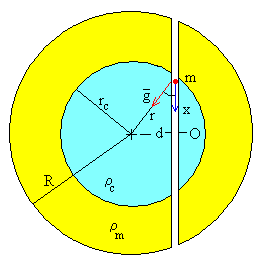 |
Se construye un túnel a lo largo de una cuerda que dista d del centro de la Tierra La fuerza que mueve la partícula a lo largo del túnel es la componente (en color azul) mg·cosθ=mg·x/r. Siendo r la distancia entre el centro de la Tierra y la partícula r2=x2+d2. |
-
La ecuación del movimiento de la partícula en el manto es
La partícula parte de la posición con velocidad nula dx/dt=0, llega al núcleo, en el instante tm con velocidad -vm, que se calculan resolviendo la ecuación diferencial de segundo orden por procedimientos numéricos.
Aplicando el principio de conservación de la energía obtenemos el mismo valor para vm que el calculado para d=0, es decir, vm=7444.3 m/s, ya que la partícula parte del reposo desde una posición que dista R del centro de la Tierra y llega a una posición que dista rc del centro de la Tierra.
-
La ecuación del movimiento en el núcleo es
En el núcleo, la partícula describe un MAS cuya frecuencia angular es la misma que la calculada en el apartado precedente
La solución de la ecuación diferencial del movimiento es
x=Asin(ωt)+Bcos(ωt)
dx/dt=Aωcos(ωt)-Bωsin(ωt)Los coeficientes A y B se determina a partir de las condiciones iniciales
Ponemos el contador de tiempo parcial a cero t=0, , dx/dt=-vm.
El tiempo que tarda en llegar al origen x=0 es
El tiempo que pasa la partícula en el interior del núcleo 4·tc, va disminuyendo a medida que aumenta d.
Aplicando el principio de conservación de la energía calculamos la velocidad con la que llega la partícula al origen. La partícula parte del reposo desde una posición que dista R del centro de la Tierra y llega a una posición que dista d del centro de la Tierra.
Por ejemplo si d=0.2R=1.274·106 m, v=9373.4 m/s
A partir de aquí, la partícula describe un MAS, hasta que llega a la frontera entre el núcleo y el manto , con velocidad –vm. En el manto, se frena la partícula hasta que llega a en reposo, completando medio ciclo de oscilación. El periodo es P=4(tc+tm)
Aproximación
Si tomamos la aceleración de la gravedad en el manto constante gm, la componente de la fuerza sobre la partícula a lo largo del túnel -gm·x/r deja de ser constante. Por lo que la ecuación del movimiento se ha de integrar aplicando procedimientos numéricos.
Caso particular d>rc
La partícula no toca el núcleo, su movimiento transcurre en el manto. La ecuación del movimiento de la partícula en el manto es
La partícula parte de la posición con velocidad nula dx/dt=0, y llega al origen x=0, en el instante tm con velocidad -vm, que se calculan resolviendo la ecuación diferencial de segundo orden por procedimientos numéricos. El periodo es P=4·tm
Aplicando el principio de conservación de la energía calculamos la velocidad con la que llega la partícula al origen. La partícula parte del reposo desde una posición que dista R del centro de la Tierra y llega a una posición que dista d del centro de la Tierra en el interior del manto.
Para llegar a esta expresión se ha empleado la relación entre las densidades del manto ρm, núcleo ρc y media ρ.
Por ejemplo si d=0.6R=3.823·106 m, v=6965.3 m/s
Actividades
Se introduce
La distancia d, del túnel al centro de la Tierra, actuando en la barra de desplazamiento titulada Distancia al centro
Se pulsa el botón titulado Empieza
Se observa el movimiento de la partícula en el túnel que atraviesa la Tierra, cuando parte del reposo en uno de los extremos del túnel. Una flecha indica la componente de fuerza de atracción sobre la partícula a lo largo del túnel.
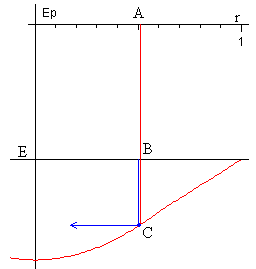 |
Se representa la función energía potencial Ep(r) en el núcleo y en el manto.
La pendiente de la curva cambiada de signo, nos proporciona el valor y sentido de la fuerza de atracción que ejerce la Tierra sobre la partícula, una flecha horizontal de color azul. |
Se proporciona los datos del
- Tiempo t, en minutos
- La posición x/R a lo largo del túnel, una fracción del radio R de la Tierra
- La velocidad v de la partícula en m/s
Los datos del modelo del interior de la Tierra son:
-
G=6.67·10-11 N·m2/kg2,
-
Densidad del núcleo ρc=11000 kg/m3,
-
Densidad del manto ρm=4437 kg/m3,
-
Radio del núcleo rc=3.490·106 m
-
Radio de la Tierra R=6.371·106 m
Referencias
Snyder R. Two-density model of the Earth. Am. J. Phys. 54 (6) June
1986, pp. 511-513![]()
