Trayectoria de un proyectil disparado desde una altura h sobre la superficie de la Tierra.
En el capítulo de Cinemática estudiamos el movimiento de los proyectiles que describen trayectorias parabólicas en el plano horizontal local, suponiendo que la aceleración de la gravedad es constante.
En la página titulada “El descubrimiento de la Ley de la Gravitación Universal”, observamos que un proyectil disparado desde una cierta altura describe una trayectoria elíptica en uno de cuyos focos está el centro de la Tierra. Las trayectorias parabólicas son aproximaciones de trayectorias elípticas, cuando el alcance y la altura máxima del proyectil son muy pequeños en comparación con el radio de la Tierra.
Supondremos también que la Tierra no gira sobre su eje. El efecto de la rotación de la Tierra se describirá en la página titulada “Desviación hacia el este de un cuerpo que cae”.
En esta página, vamos a determinar la trayectoria que sigue el proyectil que es disparado desde una altura h, con velocidad inicial v0 haciendo un ángulo φ con la dirección radial.
A lo largo de esta página, necesitaremos los siguientes datos:
-
El radio de la Tierra R=6.37·106 m
-
La masa de la Tierra M=5.98·1024 kg
-
La constante G=6.67·10-11 Nm2/kg2
Ecuación de la trayectoria
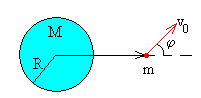 Se dispara un proyectil de masa m desde una
distancia r0=R+h del centro de la Tierra, con
velocidad v0 haciendo un ángulo φ con el radio
vector. El momento angular y la energía del proyectil son,
respectivamente
Se dispara un proyectil de masa m desde una
distancia r0=R+h del centro de la Tierra, con
velocidad v0 haciendo un ángulo φ con el radio
vector. El momento angular y la energía del proyectil son,
respectivamente
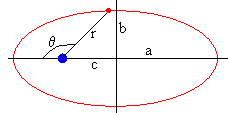 La ecuación de la trayectoria en coordenadas
polares es
La ecuación de la trayectoria en coordenadas
polares es
La semidistancia focal, c=ε·a
El semieje menor b de la elipse
Velocidad del proyectil en el punto de impacto
Como la energía es constante en todos los puntos de la trayectoria, la velocidad v con la que impacta el proyectil en la superficie de la Tierra es independiente de la masa m del proyectil y del ángulo de disparo. Se obtiene poniendo r=R (radio de la Tierra) en la ecuación de la energía, y despejando la incógnita v
Tiempo de vuelo
Para calcular el tiempo de vuelo, vamos a utilizar el mismo procedimiento que empleamos para deducir la fórmula del periodo de un planeta, a partir de la ley de las áreas. El momento angular en coordenadas polares se escribe
Integrando
El primer miembro, es el área barrida por el radio vector cuando se mueve desde la posición angular θ, a la posición θ=π. Despejando t se obtiene.
Vamos ahora a estudiar los distintos casos que se pueden presentar
El ángulo de disparo es φ=0º.
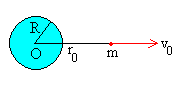 El momento angular L=0, por lo que la
trayectoria es una línea recta que pasa por el centro de fuerzas. El
proyectil asciende y luego cae hacia la Tierra a lo largo de la dirección
radial.
El momento angular L=0, por lo que la
trayectoria es una línea recta que pasa por el centro de fuerzas. El
proyectil asciende y luego cae hacia la Tierra a lo largo de la dirección
radial.
La máxima altura que alcanza, se calcula poniendo v=0 en la ecuación de la energía y se despejando la incógnita r.
No podemos calcular de forma simple el tiempo que tarda el proyectil en impactar sobre la superficie de la Tierra ya que la aceleración no es constante.
Ejemplo
Lanzamos un proyectil desde la altura h=6000 km con velocidad inicial v0= 4500 m/s en la dirección radial r0=6.0·106+6.37·106 m
-
La altura máxima que alcanza el proyectil es h=18.03·106 -6.37·106=11.66·106 m
-
La velocidad con la que llega a la superficie de la Tierra es v=8999.6 m/s
El ángulo de disparo es φ=180º.
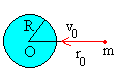 El momento angular L=0, por lo que la
trayectoria es una línea recta que pasa por el centro de fuerzas. El
proyectil desciende a lo largo de la dirección radial hasta que llega a la superficie de la Tierra con la misma velocidad que hemos calculado
en el apartado anterior.
El momento angular L=0, por lo que la
trayectoria es una línea recta que pasa por el centro de fuerzas. El
proyectil desciende a lo largo de la dirección radial hasta que llega a la superficie de la Tierra con la misma velocidad que hemos calculado
en el apartado anterior.
Ejemplo
Lanzamos un proyectil desde la posición r0=6.0·106+6.37·106 m con velocidad inicial v0= 4500 m/s en la dirección radial y sentido hacia el centro de la Tierra
-
La velocidad con la que impacta sobre la superficie de la Tierra es v=8999.6 m/s
El ángulo de disparo es φ=90º.
Alcance máximo
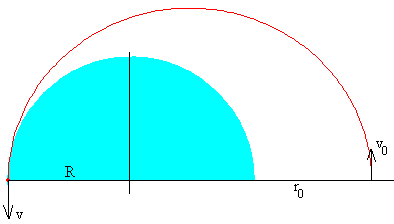
El alcance máximo se produce cuando el perigeo es R, y el apogeo es r0=h+R.
Como el momento angular y la energía son constantes en todos los puntos de la trayectoria y en particular, en el perigeo y en el apogeo, tenemos que
Los datos son r0 y R y las incógnitas v y v0. La velocidad de disparo es
Ejemplo: Sea h=6000 km o bien, la distancia a lo largo de la dirección radial es r0=12.37·106 m
Calculamos la velocidad de disparo, v0=4681.969 m/s
El semieje mayor de la elipse es a=(R+r0)/2=14.37·106 m
El tiempo de vuelo es la mitad del periodo
t=P/2=4512 s
Posición del punto de impacto
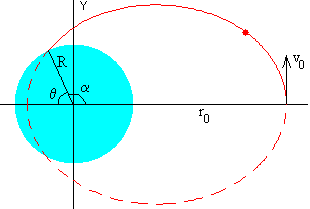
Como vemos en la figura, el proyectil sale de la posición θ=π, e impacta en la posición θ=π-α cuando r=R.
Poniendo r=R en la ecuación de la trayectoria, despejamos el ángulo θ.
Ejemplo:
Continuando con los mismos datos de los casos anteriores:
-
Distancia radial del disparo r0=12.37·106 m
-
Velocidad inicial v0= 4500 m/s
-
Angulo de disparo φ=90º.
Obtenemos los valores del momento angular y de la energía del proyectil
L=5.57·1010 m kgm2/s
E=-22.12·106 m J
Conocida la energía y el momento angular, se determina la ecuación de la trayectoria, el valor del parámetro d y la excentricidad ε
ε=0.372
d=7.77·106 m
Con estos datos, poniendo r=6.37·106 m en la ecuación de la trayectoria obtenemos el ángulo θ=0.934 rad.
La distancia angular entre el punto de impacto y la posición de disparo es
α=π-0.934=2.20 rad
Denominado alcance a la longitud del arco s de circunferencia de la Tierra que corresponde a esta distancia angular, s=R·α=14.03·106 m
Tiempo de vuelo
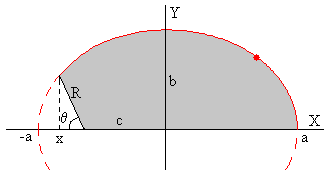
El área sombreada es el área barrida por el radio vector entre las posiciones angulares θ y π. En otras palabras, es la porción de elipse comprendida entre x y a menos el área del triángulo de base R·cosθ y altura R·senθ, siendo x=-c-R·cosθ
Sabiendo que la ecuación de la elipse es
donde a es el semieje mayor de la elipse, b el semieje menor, y c la semidistancia focal.
El área de la porción de elipse comprendida entre x y a es
Para integrar, se ha hecho el cambio de variable x=a·sen z. Los nuevos límites de integración son:
- cuando x=a, z2=π/2,
- cuando -R·cosθ-c=a·sin z1
El área sombreada vale, por tanto
Para calcular el área necesitamos los siguientes datos
-
a=9.82·106 m
-
c=3.35·106 m
-
b=8.37·106 m
A continuación, obtenemos z1 que es a función del ángulo θ=0.934 rad de la posición de impacto. Después de hacer algunas operaciones con la calculadora obtenemos el valor del área barrida por el radio vector A=1.022·1014.
Finalmente, el tiempo de vuelo t es
El ángulo de disparo es φ<90º
Trayectoria
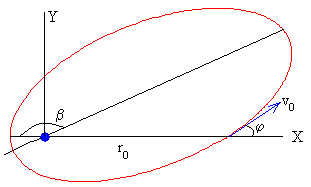
Supongamos que el ángulo de disparo es φ distinto de 0º, 90º, ó 180º.
Como vemos en la figura, la trayectoria que sigue el proyectil es una elipse, pero que está girada un ángulo β. Este ángulo se calcula poniendo r=r0 en la ecuación de la trayectoria y despejando el ángulo θ
Continuando con los datos de los casos anteriores
-
Distancia radial del disparo r0=12.37·106 m
-
Velocidad inicial v0= 4500 m/s
-
Angulo de disparo φ=30º.
La energía del proyectil no cambia, pero cambia el momento angular
L=2.78·1010 m kgm2/s
E=-22.12·106 m J
Conocida la energía y el momento angular se determina la ecuación de la trayectoria, el valor del parámetro d y la excentricidad ε
ε=0.886
d=1.94·106 m
Con estos datos calculamos el ángulo girado por el eje mayor de la elipse β=2.83 rad.
Posición del punto de impacto
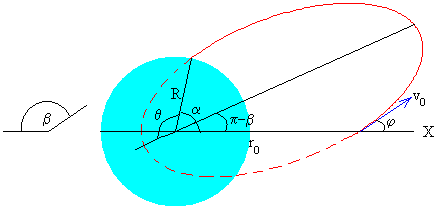
Como vemos en la figura, calculamos el ángulo de impacto poniendo en la ecuación de la elipse r=R, lo que nos da el ángulo θ señalado en la figura, del mismo modo que en el caso anterior
Relacionamos los ángulos θ, α y β. para calcular la distancia angular α entre el punto de impacto y la posición de disparo.
α=2π-θ-β
Ejemplo:
con los datos anteriores θ=2.47, y β=2.83 rad, la distancia angular α=0.981 rad (56.2º)
Tiempo de vuelo
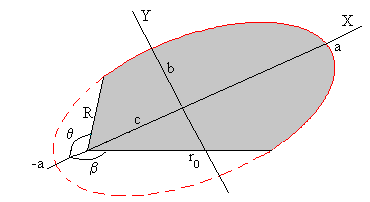
El tiempo de vuelo es proporcional a la suma de las áreas sombreadas de elipse
Las áreas se calculan como en el caso anterior. En primer lugar, necesitamos los valores de los parámetros de la elipse:
-
semieje mayor a=9.02·106 m
-
semidistancia focal c=7.99·106 m
-
semieje menor b=4.18·106 m
Calculamos el área de la porción de elipse por encima del eje mayor, que es el área barrida por el radio vector desde la posición angular θ=2.47 hasta θ=π. Necesitamos conocer previamente, z1, que es a su vez función del ángulo θ de la posición de impacto.
-R·cosθ-c=a·sin z1
El resultado es A1=5.1786·1013
Calculamos el área por debajo del eje mayor barrida por el radio vector desde la posición angular β=2.83 rad hasta β =π.
Necesitamos conocer previamente, z1, que es a su vez función del ángulo β=2.83 rad que reemplaza al ángulo θ en la fórmula del área y r0 reemplaza a R
-r0·cosβ-c=a·sin z1
El resultado es A2=3.6620·1013
El tiempo de vuelo es
El ángulo de disparo es φ>90º.
Trayectoria
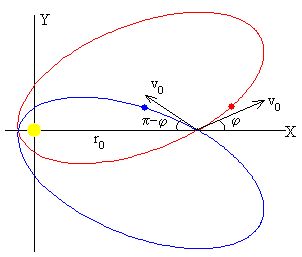
Los proyectiles disparados con ángulos φ y 180-φ tienen la misma energía y el mismo momento angular, la trayectoria es una elipse con los mismos valores del parámetro d, y de la excentricidad ε, pero su orientación es distinta.
Si el ángulo de disparo es 150º, la energía y el momento angular son los mismos que cuando se dispara el proyectil con 30º
ε=0.886
d=1.94·106 m
Como vemos en la figura, la trayectoria que sigue el proyectil es una elipse, pero que está girada un ángulo β. Este ángulo se calcula poniendo r=r0 en la ecuación de la trayectoria
Con estos datos calculamos el ángulo β=2.83 rad (color rojo) que gira el eje mayor de la elipse que es la solución que tomamos en el caso anterior, pero también es solución el ángulo β=2π-2.83=3.45 rad.(color azul)
Posición del punto de impacto
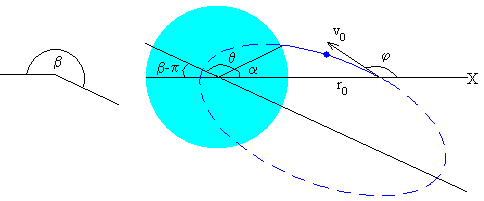
En el apartado anterior, calculamos el ángulo de impacto poniendo en la ecuación de la elipse r=R, lo que nos daba el ángulo θ=2.47 rad
Relacionamos los ángulos θ, α y β. para calcular el ángulo de impacto α.
α+θ+β-π =π o bien,
α=2π-β-θ=0.36 rad (20.4º)
que es la misma relación que obtuvimos en el caso anterior.
Tiempo de vuelo
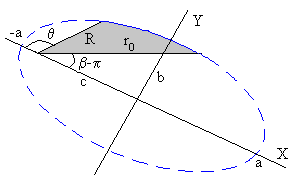
El área barrida por el radio vector desde la posición inicial de salida a la de impacto es la diferencia de dos áreas
-
El área A1 barrida por el radio vector desde la posición θ=2.47 a la posición θ=π
-
El área A2 barrida por el radio vector desde la posición angular 2π-β =2.83 a la posición π.
Estas dos áreas coinciden con las áreas A1 y A2 calculadas en el caso anterior
El tiempo de vuelo es
Actividades
Se introduce
-
La altura h en km desde la que se dispara el proyectil, en el control de edición titulado Altura. La posición inicial del proyectil es r0=h·1000+6.37·106 m
-
La velocidad de disparo v0 en m/s, en el control de edición titulado Velocidad
-
El ángulo de disparo, medido desde la dirección radial, actuando sobre el dedo de la barra de desplazamiento titulada Angulo
Se pulsa el botón titulado Empieza
Se excluyen los ángulos 0, y 180º ya que su análisis es más simple y dan lugar, a errores por desbordamiento en la rutina principal de cálculo.
Se observa el movimiento del proyectil, y se proporcionan los datos de la distancia angular entre el punto de impacto sobre la superficie de la Tierra y el lugar del lanzamiento, así como el tiempo de vuelo empleado por el proyectil.
Si la velocidad es grande, puede ocurrir que el proyectil se ponga en órbita alrededor de la Tierra.
Como ejercicios se sugiere,
-
Resolver utilizando la calculadora algún ejemplo concreto, tal como se ha hecho en estas páginas, y comprobar los resultados con los proporcionados por el programa interactivo
-
Fijando la velocidad de disparo, cambiar el ángulo de tiro, y buscar el ángulo para el cual el alcance es máximo
-
Fijada la altura de disparo, buscar la velocidad que hace que el proyectil describa una órbita circular alrededor de la Tierra.
