• Inicio
• Dinámica celeste
• Fuerza central y conservativa

Trayectoria de un proyectil disparado desde la superficie de la Tierra

En el capítulo de Cinemática estudiamos el movimiento de los proyectiles que describen trayectorias parabólicas en el plano horizontal local, suponiendo que la aceleración de la gravedad es constante.

En esta página, vamos a determinar la trayectoria que sigue el proyectil que es disparado desde la superficie de la Tierra con velocidad inicial v₀ haciendo un ángulo φ con el plano horizontal local.

Ecuación de la trayectoria

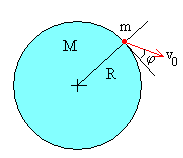El momento angular y la energía de un proyectil de masa m lanzado desde una distancia R del centro de la Tierra, con velocidad v₀ haciendo un ángulo 90-φ con la dirección radial es

${\displaystyle \begin{array}{l}L=mR{v}_0\cos \varphi \\ E=\frac{1}{2}m{v}_0^2-\frac{GMm}{R}\end{array}}$

que se mantienen constantes en todos los puntos de la trayectoria.

La ecuación de la trayectoria en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }\epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}d=\frac{L^2}{GM{m}^2}}$

La ecuación de la trayectoria es independiente de la masa m del proyectil.

Si la energía del proyectil es negativa E<0 la trayectoria es una elipse. La velocidad de disparo v₀ debe ser menor que la velocidad de escape v_e

${\displaystyle \frac{1}{2}m{v}_e^2-G\frac{Mm}{R}=0v_e=\sqrt{\frac{2GM}{R}}=11190.7\text{m/s}}$

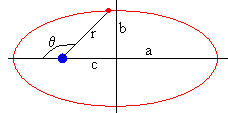Conocido d y ε, se calcula

• El semieje mayor a, que es la media aritmética de los radios mínimo (θ=0)  y máximo (θ=π) de la elipse.

${\displaystyle 2a=\frac{d}{1+\epsilon }+\frac{d}{1-\epsilon }a=\frac{d}{1-{\epsilon }^2}}$

• La semidistancia focal c=ε·a

• El semieje menor b de la elipse $b=\sqrt{a^2-c^2}$

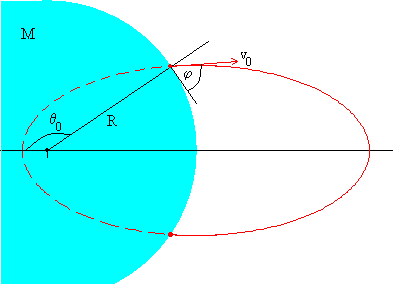
En coordenadas polares, el proyectil sale de la posición R, θ₀, y llega a la posición R, -θ₀, donde

${\displaystyle R=\frac{d}{1+\epsilon \cos {\theta }_0}\cos {\theta }_0=\frac{d-R}{R\epsilon }}$

El alcance del proyectil, es la medida del arco a lo largo de la superficie de la Tierra entre la posición de disparo y la de impacto 2·R·(π-θ₀)

La distancia máxima al centro de la Tierra se calcula en la ecuación de la elipse en coordenadas polares con θ=π.

${\displaystyle r_{máx}=\frac{d}{1-\epsilon }}$

La altura máxima sobre la superficie de la Tierra es h_máx=r_máx-R

Tiempo de vuelo

Para calcular el tiempo de vuelo, vamos a utilizar el mismo procedimiento que empleamos para deducir la fórmula del periodo de un planeta, a partir de la ley de las áreas.

El momento angular en coordenadas polares se escribe

${\displaystyle L=m{r}^2\frac{d\theta }{dt}}$

Integrando

${\displaystyle {\displaystyle \underset{{\theta }_0}{\overset{\pi }{\int }}\frac{1}{2}{r}^{2}d\theta }={\displaystyle \underset{0}{\overset{t}{\int }}\frac{L}{2m}dt}}$

El primer miembro, es el área barrida por el radio vector cuando el proyectil se mueve desde la posición angular θ=θ₀, a la posición θ=π. El tiempo de vuelo t se obtiene.

${\displaystyle t=2\frac{2m·\text{Area}}{L}}$

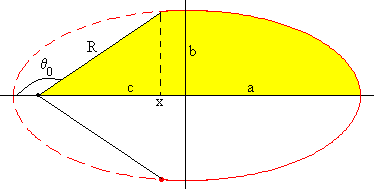
El área sombreada es el área de la porción de elipse comprendida entre x y a más el área del triángulo de base R·cos(π-θ₀) y altura R·sin(π-θ₀), siendo x=-c+R·cos(π-θ₀)

Sabiendo que la ecuación de la elipse es

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$  

donde a es el semieje mayor de la elipse, b el semieje menor, y c la semidistancia focal.

El área de la porción de elipse comprendida entre x y a es

${\displaystyle {\displaystyle \underset{x}{\overset{a}{\int }}b\sqrt{1-\frac{x^2}{a^2}}dx}={\displaystyle \underset{z_1}{\overset{z_2}{\int }}ab{\cos }^{2}z·dz}=\frac{ab}{2}{\left[z+\frac{1}{2}\text{sin}2z\right]}_{z_1}^{z_2}=\frac{ab}{2}\left(\frac{\pi }{2}-z_1-\frac{1}{2}\text{sin}2z_1\right)}$

Para integrar, se ha hecho el cambio de variable x=a·sin z. Los nuevos límites de integración son:

• cuando x=a, z₂=π/2,
• cuando -c-R·cosθ₀=a·sinz₁

El área sombreada vale, por tanto

${\displaystyle \text{Area}=\frac{ab}{2}\left(\frac{\pi }{2}-z_1-\frac{1}{2}\text{sin}2z_1\right)-\frac{R^2\text{sin}2{\theta }_0}{4}}$

Caso particular:

El ángulo de disparo es φ=90º.

El momento angular L=0, por lo que la trayectoria es una línea recta que pasa por el centro de fuerzas. El proyectil asciende y desciende cayendo hacia la Tierra a lo largo de la dirección radial.

La máxima altura que alcanza, se calcula poniendo v=0 en la ecuación de la energía y se despejando la incógnita r.

${\displaystyle E=\frac{1}{2}m{v}_0^2-\frac{GMm}{R}=-\frac{GMm}{r}}$

No podemos calcular de forma simple el tiempo que tarda el proyectil en volver a la superficie de la Tierra ya que la aceleración no es constante.

Ejemplos

1.-Disparamos un proyectil desde algún lugar de la superficie de la Tierra con velocidad inicial v₀= 7500 m/s a lo largo de la dirección radial

Los datos del problema son los siguientes:

• El radio de la Tierra R=6.37·10⁶ m
• La masa de la Tierra M=5.98·10²⁴ kg
• La constante G=6.67·10^-11 Nm²/kg²

La máxima distancia al centro de la Tierra que alcanza el proyectil es r=11.56·10⁶ m=1.815 radios terrestres

La altura máxima es h=r-R=5.20·10⁶ m

2.-Disparamos un proyectil desde algún lugar de la superficie de la Tierra con velocidad inicial v₀= 7500 m/s en la dirección que hace φ=60º con el plano local

La energía del proyectil y el momento angular valen

L=6.37·10⁶·7500·cos60º=2.39 ·10¹⁰ m kgm²/s

${\displaystyle E=\frac{1}{2}m{7500}^2-\frac{6.67·{10}^{-11}·5.98·{10}^{24}m}{6.37·{10}^6}=-34.49·{10}^6·m\text{J}}$

Trayectoria

Conocidos los valores de la energía E y del momento angular L, calculamos el valor del parámetros geométricos de la elipse: d y la excentricidad ε

ε=0.867
d=1.43·10⁶ m 

Con estos datos calculamos el ángulo θ₀.

${\displaystyle \cos {\theta }_0=\frac{1.43·{10}^6-6.37·{10}^6}{6.37·{10}^6·0.867}{\theta }_0=153.4º}$

El alcance del proyectil es 2·R·(π-θ₀)= 2·6.37·10⁶·(π-2.68)=6.20·10⁶ m

Tiempo de vuelo

Para calcular el tiempo de vuelo tenemos que calcular primero el área barrida por el radio vector desde la posición angular θ=θ₀, a la posición θ=π sombreada de elipse y multiplicarla por dos

En primer lugar, necesitamos los valores de los parámetros de la elipse:

• semieje mayor a=5.78·10⁶ m

• semieje menor b=2.88·10⁶ m

a·sinz₁=-c-R·cosθ₀        z₁=6.73º=0.117 rad

${\displaystyle \text{Area}=\frac{ab}{2}\left(\frac{\pi }{2}-z_1-\frac{1}{2}\text{sin}2z_1\right)-\frac{R^2\text{sin}2{\theta }_0}{4}}$

Area=1.925·10¹³

El tiempo de vuelo es

${\displaystyle t=2\frac{2m·\text{Area}}{L}=3223.1\text{s}}$

Actividades

Se introduce

• La velocidad de disparo v₀, actuando en la barra de desplazamiento titulada Velocidad.

• El ángulo de tiro φ, con la horizontal local, actuando en la barra de desplazamiento titulada Ángulo.

Se pulsa el botón titulado Empieza

Se observa la trayectoria seguida por el proyectil. En la parte superior derecha del applet, se proporcionan los datos de la distancia al centro de la Tierra medido en radios terrestres y el tiempo en segundos.

Curso Interactivo de Física en Internet © Ángel Franco García