Movimiento relativo de dos cuerpos en órbitas alrededor de la Tierra

Hemos estudiado que las naves espaciales describen órbitas elípticas en uno de cuyos focos está el centro de la Tierra. Supongamos que una nave espacial describe una órbita circular de radio r₀. En un momento dado, se lanza un cuerpo con una velocidad u relativa a la nave espacial en cualquier dirección, contenida en el plano de su órbita. Supondremos el cuerpo es pequeño de modo que su lanzamiento no altera apreciablemente la trayectoria circular de la nave espacial.

Vamos a comprobar la complejidad de las trayectorias que describe el cuerpo visto por un astronauta que viaja en la nave espacial. Finalmente, efectuaremos algunas aproximaciones para describirlas de forma analítica

Movimiento circular de la nave espacial alrededor de la Tierra

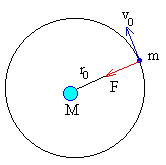
Aplicamos la ecuación de la dinámica del movimiento circular, para calcular la velocidad de la nave espacial de masa m que describe un movimiento circular de radio r₀.

$m \frac{v_{0}^{2}}{r_{0}} = G \frac{M m}{r_{0}^{2}} v_{0} = \sqrt{\frac{G M}{r_{0}}}$

donde G=6.67·10^-11 Nm²/kg², y M=5.98·10²⁴ kg es la masa de la Tierra y R=6.37·10⁶ m es su radio.

Ejemplo:

Supongamos que la nave espacial describe una órbita circular a una altura de 4000 km por encima de la superficie de la Tierra r₀=6.37·10⁶+4.0·10⁶=10.37·10⁶ m

$v_{0} = \sqrt{\frac{G M}{r_{0}}} v_{0} = \sqrt{\frac{6.67 \cdot 10^{- 11} \cdot 5.98 \cdot 10^{24}}{10.37 \cdot 10^{6}}} = 6202 m/s$

El tiempo que tarda en dar una vuelta es

P₀=2πr₀/v₀=10506 s

Movimiento del cuerpo que está a una cierta altura sobre la nave espacial

Consideremos primero, el caso más simple, el movimiento de un cuerpo que está a una distancia h de la nave espacial medida a lo largo de la dirección radial y que en el instante inicial, tiene su misma velocidad. Se suelta el cuerpo y comprobamos que ambos se mueven en órbitas distintas.

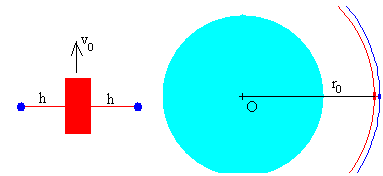
Vamos a considerar dos casos que h sea positiva, la altura del cuerpo sea mayor que el de la nave espacial, y que h sea negativa, la altura del cuerpo sea menor que la de la nave espacial.

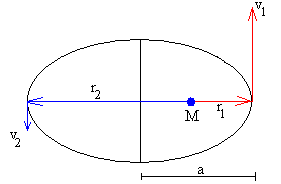La constancia del momento angular y de la energía del cuerpo nos permiten calcular la distancia máxima o mínima r₂ y su velocidad v₂, conocidas la distancia mínima o máxima r₁=r₀+h y su velocidad v₁=v₀.

$\begin{array}{l} m v_{1} r_{1} sin 90 = m v_{2} r_{2} sin 90 \\ \frac{1}{2} m v_{1}^{2} + (- G \frac{M m}{r_{1}}) = \frac{1}{2} m v_{2}^{2} + (- G \frac{M m}{r_{2}}) \end{array}$

Despejamos v₂ y r₂

$v_{2} = \frac{2 G M}{r_{1} v_{1}} - v_{1} r_{2} = \frac{r_{1} v_{1}}{v_{2}}$

El semieje mayor de la elipse es a=(r₁+r₂)/2 y el periodo P, o tiempo que tarda el cuerpo en dar una vuelta completa es

$P^{2} = \frac{4 π^{2}}{G M} a^{3}$

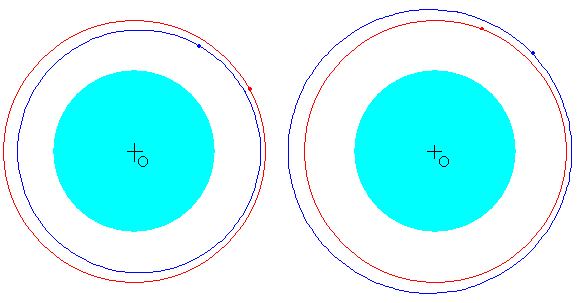
En la figura, vemos la trayectoria seguida por un cuerpo sujeto a la nave espacial y que se suelta en el instante inicial con la misma velocidad v₀ que lleva la nave. En la figura de la izquierda, la altura del objeto es menor que el de la nave espacial, h<0, el cuerpo va por delante de la nave. En la figura de la derecha, la altura del objeto es mayor que el de la nave espacial, h>0, el cuerpo va por detrás de la nave.

Ejemplo:

El cuerpo está por encima de la nave espacial

La nave espacial dista r₀=6.37·10⁶+4.0·10⁶=10.37·10⁶ m, del centro de la Tierra (o bien, 4000 km de altura sobre la superficie de la Tierra) y sea h=80·10³ (el cuerpo está 80 km por encima de la nave espacial)

La velocidad de la nave espacial como hemos calculado en el apartado anterior es de v₀=6202 m/s y el tiempo que tarda en dar una vuelta es P₀=2πr₀/v₀=10506 s

Dado r₁=r₀+h=10.37·10⁶+80·10³=10.45·10⁶ m, y v₁=6202 m/s calculamos v₂ y r₂

$v_{2} = \frac{2 \cdot 6.67 \cdot 10^{- 11} \cdot 5.98 \cdot 10^{24}}{10.45 \cdot 10^{6} \cdot 6202} - 6202 = 6107 m/s r_{2} = \frac{10.45 \cdot 10^{6} \cdot 6202}{6107} = 10.61 \cdot 10^{6} m$

El semieje mayor de la elipse vale a=(10.45·10⁶ +10.61·10⁶)/2=10.53·10⁶ m, y el periodo

$P^{2} = \frac{4 π^{2}}{6.67 \cdot 10^{- 11} \cdot 5.98 \cdot 10^{24}} {(10.53 \cdot 10^{6})}^{3} P = 10752 s$

Como el semieje es mayor que el radio de la órbita circular a>r₀, el periodo P del movimiento del cuerpo es mayor que el de la nave espacial P₀. El cuerpo va por detrás de la nave espacial

El cuerpo está por debajo de la nave espacial

Dado r₁=r₀-h=r₁=r₀+h=10.37·10⁶-80·10³=10.29·10⁶ m, y v₁=6202 m/s calculamos v₂ y r₂

$v_{2} = \frac{2 \cdot 6.67 \cdot 10^{- 11} \cdot 5.98 \cdot 10^{24}}{10.29 \cdot 10^{6} \cdot 6202} - 6202 = 6298 m/s r_{2} = \frac{10.29 \cdot 10^{6} \cdot 6202}{6298} = 10.13 \cdot 10^{6} m$

El semieje mayor de la elipse vale a=(10.29·10⁶ +10.13·10⁶)/2=10.21·10⁶ m, y el periodo P=10266 s que es menor que el periodo P₀ de la nave espacial. El cuerpo va por delante de la nave espacial.

Posición relativa del cuerpo respecto de la nave espacial

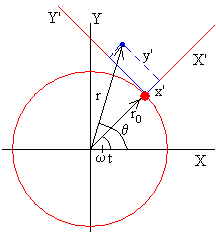La posición del cuerpo respecto del Sistema de Referencia Inercial situado en el centro de la Tierra es

x=r·cos(θ)
y=r·sin(θ)

donde r y θ son funciones del tiempo t, véase la ecuación de la trayectoria

La posición del cuerpo visto por un astronauta que viaja en la nave espacial o bien, respecto del Sistema de Referencia no Inercial OX’Y’ es

x’=r·cos(θ-ωt)-r₀y’=r·sin(θ-ωt)

siendo ω=v₀/r₀ la velocidad angular de rotación constante de la nave espacial y r₀ el radio de su órbita.

En el Sistema de Referencia no Inercial el eje X' es la dirección radial, y el eje Y' es la dirección tangente a la circunferencia de radio r₀. Si x'>0 el cuerpo está por encima de la nave espacial, y si x'<0 el cuerpo está por debajo. Si y'>0 el cuerpo se mueve por delante y si y'<0 el cuerpo se mueve detrás de la nave espacial.

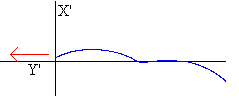En la figura, el cuerpo tiene inicialmente, una altura mayor que la nave espacial. Desde el punto de vista del astronauta, el cuerpo va por detrás de la nave espacial y su distancia se va agrandando con el paso del tiempo en la dirección tangencial Y'. La flecha roja indica la dirección y sentido del movimiento de la nave.

Actividades

Se introduce

La altura en km de la nave espacial sobre la superficie de la Tierra, en el control de edición titulado Altura
La distancia h en km, medida a lo largo de la dirección radial entre la nave espacial y el cuerpo en el instante inicial, actuando en la barra de desplazamiento titulada Distancia.

Se pulsa el botón titulado Empieza

En la parte izquierda del applet, se representa el movimiento de los dos cuerpos alrededor de la Tierra:

La nave espacial, es un punto de color rojo en órbita circular alrededor de la Tierra
El cuerpo, es un punto de color azul que describe una trayectoria elíptica

A la derecha del applet, se representa la trayectoria seguida por el cuerpo vista por un astronauta que viaja en la nave espacial.

El eje vertical X' es la dirección radial y nos indica si el cuerpo está por encima o por debajo de la nave espacial.
El eje horizontal Y' es la dirección tangencial a la órbita de la nave espacial y nos indica si el cuerpo está por delante o por detrás de la nave espacial.

Las distancias tanto en el eje horizontal Y' como en el vertical X' están expresadas en km.

Para poder ver adecuadamente la trayectoria, se puede elegir la escala en el control de selección titulado Escala y a continuación, se pulsa el botón titulado Empieza.