Un depósito de arena que se mueve sobre una pista horizontal

En esta página, se estudia el movimiento de un depósito inicialmente lleno de arena, cuando se abre un orificio en el fondo del depósito

En el primer caso, el depósito se mueve sobre una pista horizontal sin rozamiento, bajo la acción de un fuerza constante.
En el segundo caso, se mueve por una pista horizontal con rozamiento, bajo la acción de la fuerza variable.

En la página anterior "Flujo de arena" se ha estudiado el flujo de arena a través de un orificio practicado en la parte inferior de un depósito estacionario. Supondremos que el flujo vertical de arena no se modifica cuando el depósito se mueve en la dirección horizontal.

Movimiento de un depósito bajo la acción de una fuerza constante

En la figura, se muestra un depósito cilíndrico de radio R, que tiene un orificio en su base inferior de radio r.

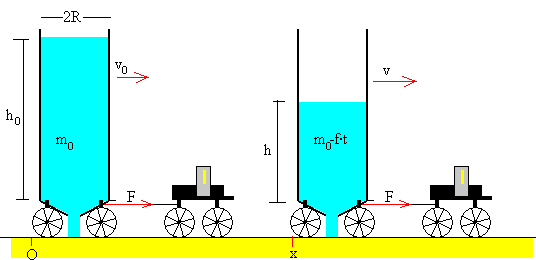
La masa del depósito en función del tiempo

La masa del depósito vacío es M, se llena con arena hasta una altura h₀. La masa inicial del depósito es

m₀=M+ρ·πR²·h₀

donde ρ es la densidad de la arena

En la página titulada "El flujo de arena" mostramos que el flujo f=dm/dt de arena a través del orificio es constante e independiente de su altura h en el depósito. La masa del depósito disminuye linealmente con el tiempo. En el instante t vale

m=m₀-f·t

o bien,

m=M+ρ·πR²·h

donde

$h = h_{0} - \frac{f \cdot t}{ρ π R^{2}}$

El depósito se vacía cuando h=0, es decir, en el instante t_m

$t_{m} = \frac{ρ π R^{2} h_{0}}{f}$

Movimiento del depósito

La segunda ley de Newton para el movimiento en una dimensión se escribe

$F = \frac{d p}{d t}$

donde p es el momento total del sistema y F la fuerza neta que actúa sobre el mismo. Como la masa del sistema varía con el tiempo, hemos de ser muy cuidadosos cuando nos referimos al momento p, ya que incluye el momento de la masa expulsada, tal como vimos en la formulación de las ecuaciones del movimiento de un cohete, que volvemos a reproducir en esta página.

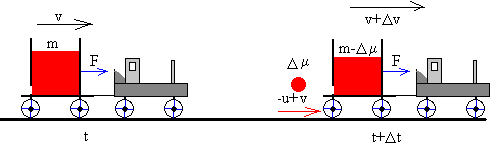
En el instante t el depósito de masa m lleva una velocidad v. Su momento lineal es

p(t)=mv

En el instante t+Δt

El depósito tiene una masa m-Δμ, su velocidad es v+Δv.
La masa de arena descargada Δμ lleva una velocidad –u respecto del depósito o una velocidad –u+ v, respecto de Tierra

El momento lineal del sistema en este instante es

p(t+Δt)=(m-Δμ)(v+Δv)+ Δμ(–u+ v)

La variación del momento lineal entre el instante t y el instante t+Δt es

Δp= p(t+Δt)- p(t)=m·Δv- u·Δμ-Δv·Δμ

En el límite cuando Δt→0

$\frac{d p}{d t} = m \frac{d v}{d t} - u \frac{d μ}{d t}$

La masa M del sistema formado por el depósito m y la arena descargada μ es constante M=μ+m, por lo que dμ+dm=0. La masa del depósito disminuye en dm y aumenta la masa de la arena descargada en la misma cantidad.

$\frac{d p}{d t} = m \frac{d v}{d t} + u \frac{d m}{d t}$

Si la velocidad u de salida de la arena respecto del depósito es cero, la ecuación del movimiento se escribe

$m \frac{d v}{d t} = F$

que es similar a la expresión para el caso de una masa constante, pero con la importante diferencia de que la masa es variable con el tiempo.

También, es similar a la ecuación del movimiento de un cohete de empuje constante, donde F=u·D es la fuerza de empuje que proporcionan los gases al quemarse.

$(m_{0} - f \cdot t) \frac{d v}{d t} = F$

Supondremos que el depósito se mueve con velocidad inicial v₀, en el instante inicial t=0, en el que se abre el orificio de salida de la arena.

$v - v_{0} = \int_{0}^{t} \frac{F}{m_{0} - f t} d t v = v_{0} + \frac{F}{f} \ln \frac{m_{0}}{m_{0} - f \cdot t}$

Integrando de nuevo, obtenemos la expresión de la posición del móvil en función del tiempo. Recordando que

$\int \ln z \cdot d z = z \cdot \ln z - z$

obtenemos

$x = v_{o} t + \frac{F}{f} t \cdot \ln m_{0} + \frac{F}{f^{2}} ((m_{0} - f t) \ln (m_{0} - f t) + f \cdot t - m_{0} \ln m_{0})$

Cuando se agota la arena del depósito, la masa del depósito vacío m=m₀-f·t_m es constante, y la aceleración es constante

$a = \frac{F}{m_{0} - f t_{m}}$

Las ecuaciones del movimiento uniformemente acelerado son.

$\begin{array}{l} v = v_{1} + a (t - t_{m}) \\ x = x_{1} + v_{1} (t - t_{m}) + \frac{1}{2} a {(t - t_{m})}^{2} \end{array}$

Donde x₁ y v₁ es la posición del depósito en el instante t_m en el que se vacía el depósito de arena

Cuando no se aplica fuerza alguna

Cuando no se aplican fuerzas, podíamos pensar erróneamente que al disminuir el depósito su masa, su velocidad se iba a incrementar. Pero nos olvidamos del momento lineal de la arena expulsada. De acuerdo a la ecuación del movimiento, si F=0, la velocidad del depósito es constante e igual a la velocidad inicial v₀.

Energías

La energía cinética inicial del depósito es

$\frac{1}{2} m_{0} v_{0}^{2}$

La energía cinética del depósito en el instante t es

$\frac{1}{2} {(m_{0} - f t)}^{2} v^{2}$

La energía cinética de la arena descargada hasta el instante t es.

$\int_{0}^{t} \frac{1}{2} d m \cdot v^{2} = \frac{1}{2} f \int_{0}^{t} v^{2} d t$

Recuérdese que la velocidad de la porción dm de arena descargada es cero respecto del depósito y v respecto de Tierra.

El trabajo realizado por la fuerza constante F es

F·x

Podemos comprobar, que el trabajo de la fuerza F se invierte en incrementar la energía cinética del depósito y de la arena descargada.

$F \cdot x = \frac{1}{2} (m_{0} - f t) v^{2} + \frac{1}{2} f \int_{0}^{t} v^{2} d t - \frac{1}{2} m_{0} v_{0}^{2}$

Para comprobarlo, nos podemos ayudar de las integrales

$\begin{array}{l} \int \ln z \cdot d z = z \cdot \ln z - z \\ \int \ln^{2} z \cdot d z = z \cdot \ln^{2} z - 2 z \cdot \ln z + 2 z \end{array}$

Ejemplo

Masa del depósito vacío M=50 kg
Altura inicial de la arena en el depósito h₀=45 cm
Flujo f=0.76 kg/s.
Fuerza F=0.7 N
Radio de la base del depósito cilíndrico R=10 cm
Densidad de la arena ρ=2500 kg/m³
Velocidad inicial del depósito v₀=0.1 m/s

La masa inicial del depósito lleno de arena es

m₀=M+ρ·πR²·h₀

m₀=50+2500·π·0.1²·0.45=85.3 kg

El tiempo que tarda en vaciarse el depósito

$t_{m} = \frac{ρ π R^{2} h_{0}}{f} t_{m} = \frac{2500 π {0.1}^{2} 0.45}{0.76} = 46.5 s$

En el instante t_m el depósito se ha vaciado, su masa es M=50 kg. La velocidad final que alcanza el depósito vacío en este instante es

$v = v_{0} + \frac{F}{f} \ln \frac{m_{0}}{m_{0} - f \cdot t_{m}} v = 0.1 + \frac{0.7}{0.76} \ln \frac{85.3}{50} = 0.59 m/s$

La posición x del depósito en el instante t_m=46.5 s es

$\begin{array}{l} x = v_{o} t_{m} + \frac{F}{f} t_{m} \cdot \ln m_{0} + \frac{F}{f^{2}} ((m_{0} - f t_{m}) \ln (m_{0} - f t_{m}) + f \cdot t_{m} - m_{0} \ln m_{0}) \\ x = 0.1 \cdot 46.5 + \frac{0.7}{0.76} 46.5 \cdot \ln 85.3 + \frac{0.7}{{0.76}^{2}} (50 \ln 50 + 0.76 \cdot 46.5 - 85.3 \ln 85.3) = 15.08 m \end{array}$

A partir de este instante, el depósito se mueve con aceleración constante

$a = \frac{F}{m_{0} - f \cdot t_{m}} a = \frac{0.7}{50} = 0.014 {m/s}^{2}$

v=0.59+0.014(t-46.5)
x=15.08+0.59(t-46.5)+0.014(t-46.5)²/2

Actividades

Se pulsa el botón titulado Inicio

Se arrastra la flecha de color rojo con el puntero del ratón, para establecer la altura inicial de la arena en el depósito.
Se introduce, el flujo f=dm/dt en (kg/s), actuando en la barra de desplazamiento titulada Flujo.
Se introduce, el peso del depósito vacío M (en kg) en el control de edición titulado Peso en vacío.
Se introduce, el valor de la fuerza F en N, en el control de edición titulado Fuerza.

Datos que se han fijado en el programa interactivo

Radio de la base del depósito cilíndrico R=10 cm
Densidad de la arena ρ=2500 kg/m³
Velocidad inicial del depósito v₀=0.1 m/s

Se pulsa el botón titulado Empieza

El orificio situado en el fondo del depósito se abre y comienza a caer un flujo f constante de arena. El depósito disminuye su masa e incrementa la velocidad.

Cuando el depósito se vacía, su masa no cambia y por tanto, se mueve con aceleración constante.

Para realizar otra “experiencia” se pulsa el botón titulado Inicio, se cambia, la masa del depósito vacío, la altura inicial de la arena en el depósito, la fuerza con la que se tira del depósito y se pulsa el botón titulado Empieza.

Arrastre con el puntero del ratón la flecha de color rojo