Movimiento de un depósito de arena bajo la acción de un peso que cae.

En este apartado, se estudia un sistema en el que la masa y la fuerza aplicada cambian. Consiste en un depósito de arena que pierde masa por su parte inferior, y que se desplaza sobre dos vías paralelas, que ejercen una fuerza de rozamiento cuando el depósito se desplaza. Este depósito está unido mediante una cuerda que pasa por una polea a un cuerpo cuya masa M es constante, tal como se muestra en la figura

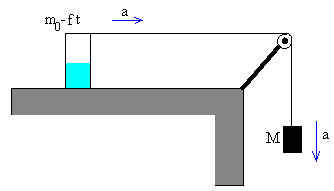
Ecuaciones del movimiento

Dibujamos las fuerzas sobre el bloque y sobre el depósito. Supondremos que la polea tiene un momento de inercia despreciable.

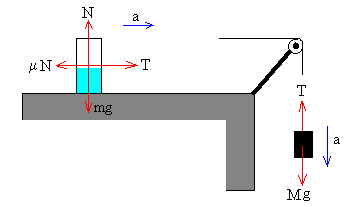
La ecuación del movimiento del depósito es

T-μN=ma
N=mg

La ecuación del movimiento del cuerpo que cuelga es

Mg-T=Ma

Primer etapa. La masa del depósito disminuye

La masa del depósito varía con el tiempo de la forma

m=m₀-f·t

Siendo m₀ la masa inicial (depósito vacío más la arena que contiene), y f el flujo constante de arena que sale por el orificio situado en su parte inferior.

Eliminando T del sistema de ecuaciones

$\frac{d v}{d t} = g \frac{M - μ m_{0} + μ f t}{M + m_{0} - f t}$

Integrando

$\int_{0}^{v} d v = \int_{0}^{t} g \frac{M - μ m_{0} + μ f t}{M + m_{0} - f t} d t$

La fracción es fácilmente integrable si se transforma en esta otra expresión equivalente

$\frac{M - μ m_{0} + μ f t}{M + m_{0} - f t} = - μ + \frac{M (1 + μ)}{M + m_{0} - f t}$

Después de hacer algunas operaciones se obtiene

$v = \frac{g M (1 + μ)}{f} \ln \frac{M + m_{0}}{M + m_{0} - f t} - μ g t$

Integrando de nuevo, obtenemos el desplazamiento x en función del tiempo t. Recordando que

$\int \ln z \cdot d z = z \ln z - z$

obtenemos

$x = \frac{g M (1 + μ)}{f} (\begin{array}{l} t (\ln (M + m_{0}) + 1) - \frac{M + m_{0}}{f} \ln (M + m_{0}) + \\ \frac{M + m_{0} - f t}{f} \ln (M + m_{0} - f t) \end{array}) - \frac{1}{2} μ g t^{2}$

Segunda etapa: la masa del depósito es constante

La arena se agota en el instante t_m. A partir de este instante, la masa del depósito es constante

m=m₀-f·t_m

La aceleración del depósito y del bloque es constante, el movimiento es uniformemente acelerado

$a = g \frac{M - μ (m_{0} - f t_{m})}{M + m_{0} - f t_{m}}$

La posición y velocidad es

$\begin{array}{l} v = v_{0} + a (t - t_{m}) \\ x = x_{0} + v_{0} (t - t_{m}) + \frac{1}{2} a {(t - t_{m})}^{2} \end{array}$

donde x₀ y v₀ es la posición y velocidad del depósito en el instante t_m en el que se quedado vacío.

Ejemplo

Masa inicial de arena 1 kg
Flujo de arena f=0.8 kg/s
Coeficiente de rozamiento μ=0.5
Masa del bloque M=1 kg.

La masa inicial del depósito de arena es igual a la masa de la arena más la masa del recipiente que lo contiene. Se ha tomado como masa del recipiente el 10% de la masa inicial de arena.

masa inicial del depósito (m₀) =1.1· masa inicial de arena

La masa inicial del depósito es m₀=1.1·1=1.1 kg

El depósito de arena se vacía en el instante t_m=1.0/0.8=1.25 s.

En dicho instante la velocidad del depósito es

$\begin{array}{l} v = \frac{g M (1 + μ)}{f} \ln \frac{M + m_{0}}{M + m_{0} - f t_{m}} - μ g t_{m} \\ v = \frac{9.8 \cdot 1 \cdot (1 + 0.5)}{0.8} \ln \frac{1 + 1.1}{1 + 1.1 - 0.8 \cdot 1.25} - 0.5 \cdot 9.8 \cdot 1.25 = 5.76 m/s \end{array}$

La posición del depósito es

$x = \frac{9.8 \cdot 1 (1 + 0.5)}{0.8} (\begin{array}{l} 1.25 (\ln (1 + 1.1) + 1) - \frac{1 + 1.1}{0.8} \ln (1 + 1.1) + \\ \frac{1 + 1.1 - 0.8 \cdot 1.25}{0.8} \ln (1 + 1.1 - 0.8 \cdot 1.25) \end{array}) - \frac{1}{2} 0.5 \cdot 9.8 \cdot {1.25}^{2} = 2.80 m$

A partir de este instante, el depósito se mueve con aceleración constante

$a = g \frac{M - μ (m_{0} - f t_{m})}{M + m_{0} - f t_{m}} a = 9.8 \frac{1 - 0.5 (1.1 - 0.8 \cdot 1.25)}{1 + 1.1 - 0.8 \cdot 1.25} = 8.46 m/s$

Las ecuaciones del movimiento son

v=5.76 +8.46·(t-1.25)
x=2.80+5.76 (t-1.25)+8.46(t-1.25)²/2

Por ejemplo, en el instante t=1.6 s el depósito se encuentra en la posición x=5.33 m y lleva una velocidad de v=8.72 m/s

Por ejemplo, el depósito llega a la posición x=4.0 m en el instante t=1.43 s, con una velocidad de v=7.31 m/s

Actividades

Se introduce

La masa de arena (en kg), en el control de edición titulado Masa de arena
El flujo f de arena (en kg/s), en el control de edición titulado Flujo de arena
El coeficiente μ de rozamiento entre le depósito y el plano horizontal, en el control de edición titulado Coef. rozamiento
La masa del bloque M, se ha fijado en el valor M=1 kg

Se pulsa el botón titulado Empieza

La masa inicial del depósito de arena es igual a la masa de la arena más la masa del recipiente que lo contiene. Se ha tomado como masa del recipiente el 10% de la masa inicial de arena.

masa inicial del depósito (m₀) =1.1· masa inicial de arena
masa final del depósito =masa del recipiente =0.1 · masa inicial de arena

El programa interactivo no comienza si se cumple que μ·m₀>M, se aconseja entonces, disminuir el valor del coeficiente de rozamiento μ.

Referencias

Sullivan P., Chaplin B, A system to change both mass and applied force. The Physics Teacher, Vol 37, May 1999, pp. 309-311