Varilla que se mueve en un campo magnético uniforme (III)

En la página anterior, hemos estudiado el movimiento de la varilla de longitud L y masa m, que se mueve sin fricción sobre dos raíles paralelos separados una distancia a. La batería cuya diferencia de potencial es V₀ , los dos raíles y la varilla deslizante constituyen un circuito cerrado. En presencia de un campo magnético uniforme B, perpendicular al plano del circuito, la barra se acelera por la fuerza de Lorentz hasta que alcanza una velocidad límite constante.

En esta página, vamos a sustituir la batería por un condensador.

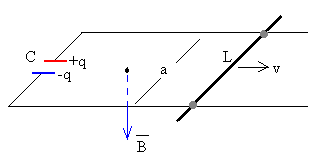
Supondremos que los raíles son superconductores, para que el problema no sea complicado de resolver. De otro modo, se introduciría un término no lineal (al aumentar o disminuir la longitud del circuito) en las ecuaciones del movimiento de la varilla.

Ecuación del circuito

La fem inducida V_ε de acuerdo a la ley de Faraday es

$V_{ε} = - \frac{d Φ}{d t}$

El flujo Φ=B·S=-B·a·x

Derivando el flujo Φ respecto del tiempo y cambiando de signo

V_ε=B·a·v

Siendo a la distancia entre los raíles, menor que la longitud L de la varilla y v la velocidad de la varilla.

El sentido de la corriente inducida, de acuerdo a la ley de Lenz, es contrario a las agujas del reloj.

En el circuito equivalente de la figura

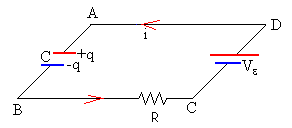
$\begin{array}{l} V_{A B} + V_{B C} + V_{C D} + V_{D A} = 0 \\ \frac{q}{C} + i R - V_{ε} = 0 \\ \frac{d q}{d t} + \frac{q}{R C} = \frac{B a v}{R} \end{array}$

Ecuación del movimiento de la varilla

Una corriente i que circula por la porción de varilla de longitud a, experimenta una fuerza F en el seno de un campo magnético uniforme B.

F=i·u_t×B·a

donde u_t es un vector unitario que señala la dirección y sentido del movimiento de los portadores de carga (positivos).

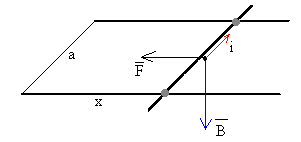
Como el campo magnético B es perpendicular a la varilla. El módulo de F es

F=iBa

Es un vector paralelo a los raíles y cuyo sentido es hacia la izquierda, tal como se señala en la figura.

Si despreciamos la fuerza de rozamiento entre la varilla y los raíles, la ecuación del movimiento de la varilla de masa m es.

$\begin{array}{l} m \frac{d v}{d t} = - i B a \\ m \frac{d v}{d t} = - \frac{d q}{d t} B a \end{array}$

Integramos esta ecuación con las condiciones iniciales siguientes: en el instante t=0, v=v₀y q=q₀. Donde v₀ es la velocidad inicial de la varilla y q₀ es la carga inicial del condensador.

$m \int_{v_{0}}^{v} d v = - B a \int_{q_{0}}^{q} d q m v = m v_{0} - B a q + B a q_{0}$

Carga del condensador

En la ecuación del circuito eliminamos v

$\begin{array}{l} \frac{d q}{d t} + \frac{q}{R C} = \frac{B a}{R} (v_{0} - \frac{B a}{m} q + \frac{B a}{m} q_{0}) \\ \frac{d q}{d t} + \frac{1}{R C} (1 + \frac{B^{2} a^{2} C}{m}) q = \frac{B a}{R} (v_{0} + \frac{B a}{m} q_{0}) \\ \frac{d q}{d t} + \frac{α}{R C} q = K \end{array}$

La solución de esta ecuación diferencial es

$q = A \exp (\frac{- α t}{R C}) + \frac{K R C}{α}$

El coeficiente A se determina a partir de la siguiente condición inicial: en el instante t=0, la carga del condensador es q₀

$q = (q_{0} - \frac{K R C}{α}) \exp (\frac{- α t}{R C}) + \frac{K R C}{α}$

Después de un tiempo grande, t→∞, la carga final del condensador es

$Q_{f} = \frac{B a C}{α} (v_{0} + \frac{B a}{m} q_{0}) α = 1 + \frac{B^{2} a^{2} C}{m}$

La carga q del condensador en función del tiempo t la expresamos

$q = (q_{0} - Q_{f}) \exp (\frac{- α t}{R C}) + Q_{f}$

Si q₀>Q_f el condensador se descarga,

$q_{0} > \frac{B a C}{α} (v_{0} + \frac{B a}{m} q_{0}) q_{0} > B a C v_{0}$

Si q₀>BaCv₀ el condensador se descarga
En caso contrario, q₀<BaCv₀ el condensador se carga

La intensidad de la corriente es

$i = \frac{d q}{d t} = \frac{- α}{R C} (q_{0} - Q_{f}) \exp (\frac{- α t}{R C})$

La intensidad de la corriente disminuye exponencialmente con el tiempo

Posición y velocidad de la varilla

De la relación

$\begin{array}{l} m v = m v_{0} - B a q + B a q_{0} \\ v = v_{0} + \frac{B a}{m} (q_{0} - Q_{f}) (1 - \exp (\frac{- α t}{R C})) \end{array}$

Después de un tiempo grande, t→∞, la velocidad final del de la varilla es

$V_{f} = v_{0} + \frac{B a}{m} (q_{0} - Q_{f}) = \frac{1}{α} (v_{0} + \frac{B a}{m} q_{0})$

Si q₀>Q_f, es decir, cuando q₀>BaCv₀ el condensador se descarga, la varilla incrementa la velocidad, V_f>v₀
Si q₀<Q_f, es decir, cuando q₀<BaCv₀ el condensador se carga, la varilla disminuye la velocidad, V_f<v₀

Integramos respecto del tiempo y obtenemos la posición de la varilla x en función del tiempo. La condición inicial es: en el instante t=0, la posición inicial de la varilla es x₀

$\begin{array}{l} \frac{d x}{d t} = v_{0} + \frac{B a (q_{0} - Q_{f})}{m} - \frac{B a (q_{0} - Q_{f})}{m} \exp (\frac{- α t}{R C}) \\ \int_{x_{0}}^{x} d x = \int_{0}^{t} v d t \\ x = x_{0} + (v_{0} + \frac{B a}{m} (q_{0} - Q_{f})) t - \frac{R C}{α} \frac{B a}{m} (q_{0} - Q_{f}) (1 - \exp (\frac{- α t}{R C})) \end{array}$

Estudio energético

La energía almacenada en forma de campo eléctrico en el condensador en el instante t=0 y el instante t es

$E_{C 0} = \frac{1}{2} \frac{q_{0}^{2}}{C} E_{C} = \frac{1}{2} \frac{q^{2}}{C}$

La energía disipada en la resistencia durante ese mismo tiempo es

$\begin{array}{l} E_{R} = \int_{0}^{t} i^{2} R \cdot d t = \int_{0}^{t} \frac{α^{2}}{R C^{2}} {(q_{0} - Q_{f})}^{2} \exp (\frac{- 2 α t}{R C}) \cdot d t = \\ = \frac{α}{2 C} {(q_{0} - Q_{f})}^{2} (1 - \exp (\frac{- 2 α t}{R C})) \end{array}$

Después de un tiempo grande, t→∞, la energía disipada en la resistencia es

$E_{R} = \frac{α}{2 C} {(q_{0} - Q_{f})}^{2} = \frac{1}{2 C α} {(q_{0} - B a C v_{0})}^{2}$

La energía cinética inicial y final de la varilla es

$E_{k 0} = \frac{1}{2} m v_{0}^{2} E_{k} = \frac{1}{2} m v^{2}$

La energía disipada en la resistencia es (en valor absoluto) la diferencia entre la energía inicial y final

E_R=(E_k0+E_C0)-(E_k+ E_C)

Se sugiere al lector que realice esta comprobación, primero para cuando t→∞ y luego, para cualquier instante t.

Ejemplos:

Capacidad, C=1.0 F
Resistencia, R=10 Ω
Campo magnético, B=0.4 T
Masa de la varilla, m=0.01 kg
Distancia entre los raíles, a=0.5 m
Carga inicial q₀=0, condensador descargado
Velocidad inicial, v₀=0.1 m/s

Carga y velocidad final después de un tiempo t→∞

$\begin{array}{l} Q_{f} = \frac{B a C}{α} (v_{0} + \frac{B a}{m} q_{0}) α = 1 + \frac{B^{2} a^{2} C}{m} \\ α = 1 + \frac{{0.4}^{2} {0.5}^{2} \cdot 1.0}{0.01} = 5 Q_{f} = \frac{0.4 \cdot 0.5 \cdot 1.0}{5} 0.1 = 0.004 C \\ V_{f} = v_{0} + \frac{B a}{m} (q_{0} - Q_{f}) V_{f} = 0.1 + \frac{0.4 \cdot 0.5}{0.01} (0 - 0.004) = 0.02 \end{array}$

Balance energético

Energía inicial

$E_{i} = \frac{1}{2} m v_{0}^{2} + \frac{1}{2} \frac{q_{0}^{2}}{C} = \frac{1}{2} 0.01 \cdot {0.1}^{2} = 5 \cdot 10^{- 5}$

Energía final, después de un tiempo t→∞

$E_{f} = \frac{1}{2} m V_{f}^{2} + \frac{1}{2} \frac{Q_{f}^{2}}{C} = \frac{1}{2} 0.01 \cdot {0.02}^{2} + \frac{1}{2} \frac{{0.004}^{2}}{1} = 1 \cdot 10^{- 5}$

Energía disipada en la resistencia

$E_{R} = \frac{α}{2 C} {(q_{0} - Q_{f})}^{2} = \frac{5}{2 \cdot 1.0} {(0 - 0.004)}^{2} = 4 \cdot 10^{- 5}$

La energía inicial es igual a la energía final más la energía disipada en la resistencia

Ejemplo 2:

Los mismos datos, cambiando la carga inicial y la velocidad inicial
Carga inicial q₀=0.02, condensador cargado
Velocidad inicial, v₀=0.0 m/s, en reposo

Carga y velocidad final después de un tiempo t→∞

$\begin{array}{l} α = 1 + \frac{{0.4}^{2} {0.5}^{2} \cdot 1.0}{0.01} = 5 Q_{f} = \frac{0.4 \cdot 0.5 \cdot 1.0}{5} (\frac{0.4 \cdot 0.5}{0.01} 0.02) = 0.016 C \\ V_{f} = \frac{0.4 \cdot 0.5}{0.01} (0.02 - 0.016) = 0.08 \end{array}$

Ejemplo 3:

Los mismos datos, cambiando la carga inicial y la velocidad inicial
Carga inicial q₀=0.02, condensador cargado
Velocidad inicial, v₀=0.1 m/s,

Carga y velocidad final después de un tiempo t→∞

$\begin{array}{l} α = 1 + \frac{{0.4}^{2} {0.5}^{2} \cdot 1.0}{0.01} = 5 Q_{f} = \frac{0.4 \cdot 0.5 \cdot 1.0}{5} (0.1 + \frac{0.4 \cdot 0.5}{0.01} 0.02) = 0.02 C \\ V_{f} = 0.1 + \frac{0.4 \cdot 0.5}{0.01} (0.02 - 0.02) = 0.1 \end{array}$

Como la carga q₀=Q_f, la intensidad es nula, no se disipa energía en la resistencia y la varilla se mueve con velocidad constante.

Ejemplo 4:

Cuando el campo B=0, la velocidad de la varilla se mantiene constante, y tenemos el caso de la descarga de un condensador a través de una resistencia.

Actividades

Se introduce

El campo magnético B ( T), en el control de edición titulado Campo magnético. Se pueden introducir valores positivos o negativos
La capacidad del condensador C (F), en el control de edición titulado Capacidad
La resistencia R (Ω) de la porción de varilla de longitud a, en el control de edición titulado Resistencia. El resto del circuito se considera superconductor
La carga inicial q₀(C) del condensador, en el control de edición titulado Carga inicial. Se pueden introducir valores positivos o negativos.
La velocidad inicial v₀ (m/s) de la varilla, en el control de edición titulado V. inicial. Se pueden introducir valores positivos o negativos.
La distancia entre los raíles se ha fijado en a=0.5 m
La masa de la varilla se ha fijado en m=0.01 kg

Se pulsa el botón titulado Empieza

En la parte superior del applet se representa, el condensador, los raíles y la varilla.

La placa positiva del condensador se representa en color rojo, y la negativa en color azul. La intensidad del color indica la cantidad de carga. El condensador descargado aparece en color blanco. Al lado del condensador se proporciona el dato de su carga.

El sentido de la corriente en el circuito, viene señalado por el movimiento de los portadores de carga (puntos de color rojo)

El campo magnético uniforme es perpendicular al plano de los raíles, apunta hacia el lector cuando está coloreado de rosa y en sentido contrario, si está coloreado de azul claro.

Al lado de la varilla se proporciona el dato de su posición

Un diagrama en forma de tarta, nos da una idea de la transformaciones energéticas:

Un sector de color rojo, representa la energía almacenada en el condensador
Un sector de color azul, representa la energía cinética de la varilla
Un sector de color negro, representa la energía disipada en la resistencia

En la parte derecha del gráfico, se representa la velocidad v de la varilla en función del tiempo. Podemos apreciar, que tiende hacia un valor constante V_f. Se puede cambiar la escala vertical mediante el control de selección situado a la derecha del botón Paso.

FemApplet aparecerá en un explorador compatible JDK 1.1

Referencias

Fatuzzo M., Toepker T. P., More track and field. The Physics Teacher Vol 42, September 2004, pp. 351-353