• Inicio
• Electromagnetismo
• Campos dependientes del tiempo

Varilla que se mueve en un campo magnético uniforme (IV)

En la página anterior, hemos estudiado el movimiento de la varilla de longitud L y masa m, que se mueve sin fricción sobre dos raíles paralelos separados una distancia a. Hemos estudiado el efecto de un condensador y de una batería, en esta página vamos a estudiar el efecto de una autoinducción.

Supondremos que los raíles son superconductores, para que el problema no sea complicado de resolver. De otro modo, se introduciría un término no lineal (al aumentar o disminuir la longitud del circuito) en las ecuaciones del movimiento de la varilla.

Resultados similares a los de esta página se dan en la situación que se estudia en las páginas tituladas "Efectos mecánicos de la ley de Faraday" y "Efectos mecánicos de la ley de Faraday. Oscilaciones amortiguadas"

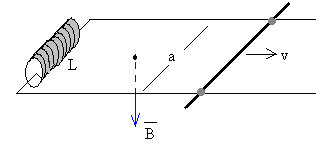
Ecuación del circuito

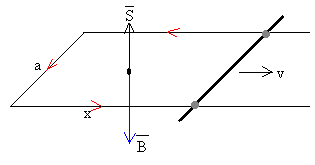
La fem inducida V_ε de acuerdo a la ley de Faraday es

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}}$

El flujo Φ=B·S=-B·a·x

Derivando el flujo Φ respecto del tiempo y cambiando de signo

V_ε=B·a·v

Siendo a la distancia entre los raíles, menor que la longitud L de la varilla y v la velocidad de la varilla.

El sentido de la corriente inducida, de acuerdo a la ley de Lenz, es contrario a las agujas del reloj.

Como la intensidad aumenta, la autoinducción es equivalente a una batería de fem Ldi/dt

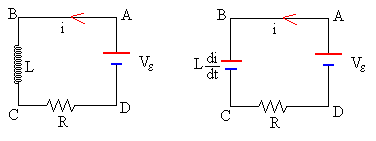
En el circuito equivalente de la figura

${\displaystyle \begin{array}{l}{V}_{AB}+V_{BC}+V_{CD}+V_{DA}=0\\ L\frac{di}{dt}+iR-V_{\epsilon }=0\end{array}}$

Ecuación del movimiento de la varilla

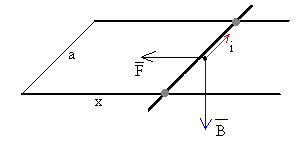
Una corriente i que circula por la porción de varilla de longitud a, experimenta una fuerza F en el seno de un campo magnético uniforme B.

F=i·u_t×B·a

donde u_t es un vector unitario que señala la dirección y sentido del movimiento de los portadores de carga (positivos).

Como el campo magnético B es perpendicular a la varilla. El módulo de F es

F=iBa

Es un vector paralelo a los raíles y cuyo sentido es hacia la izquierda, es una fuerza de frenado.

Si despreciamos la fuerza de rozamiento entre la varilla y los raíles, la ecuación del movimiento de la varilla de masa m es.

${\displaystyle m\frac{dv}{dt}=-iBa}$

La intensidad

En la ecuación del circuito derivamos respecto del tiempo

${\displaystyle \begin{array}{l}\frac{di}{dt}+iR-Bav=0\\ L\frac{d^{2}i}{d{t}^2}+R\frac{di}{dt}-Ba\frac{dv}{dt}=0\\ L\frac{d^{2}i}{d{t}^2}+R\frac{di}{dt}+\frac{B^2{a}^2}{m}i=0\\ \frac{d^{2}i}{d{t}^2}+2\gamma \frac{di}{dt}+{\omega }_0^{2}i=02\gamma =\frac{R}{L}{\omega }_0^2=\frac{B^2{a}^2}{mL}\end{array}}$

Tenemos la ecuación de una oscilación amortiguada, cuya solución es

${\displaystyle \begin{array}{l}i=A\exp (-\gamma t)\sin (\omega t+\varphi ){\omega }^2={\omega }_0^2-{\gamma }^2\\ \frac{di}{dt}=-\gamma A\exp (-\gamma t)\sin (\omega t+\varphi )+\omega A\exp (-\gamma t)\cos (\omega t+\varphi )\end{array}}$

ω es la frecuencia angular de la oscilación amortiguada, ω₀ es la frecuencia natural del oscilador y γ es la constante de amortiguamiento

La amplitud inicial A y la fase inicial φ se determina  a partir de las condiciones iniciales. En nuestro caso son:

En el instante t=0, la velocidad inicial de la varilla es v₀, la intensidad es nula, i=0.

De la ecuación del circuito tenemos que en el instante t=0.

${\displaystyle \begin{array}{l}L\frac{di}{dt}+iR-Bav=0\\ \frac{di}{dt}=\frac{Ba{v}_0}{L}\end{array}}$

La amplitud inicial A y la fase inicial φ valen

${\displaystyle \begin{array}{l}0=A\sin \varphi \\ \frac{Ba{v}_0}{L}=-\gamma A\sin \varphi +\omega A\cos \varphi \\ \varphi =0A=\frac{Ba{v}_0}{\omega L}\end{array}}$

La intensidad que circula por la varilla en función del tiempo es

${\displaystyle i=\frac{Ba{v}_0}{\omega L}\exp (-\gamma t)\sin (\omega t)}$

Posición y velocidad de la varilla

De la ecuación del movimiento de la varilla

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-Bai\\ \frac{dv}{dt}=-\frac{B^2{a}^2{v}_0}{m\omega L}\exp (-\gamma t)\sin (\omega t)\\ \frac{dv}{dt}=-{\omega }_0^2\frac{v_0}{\omega }\exp (-\gamma t)\sin (\omega t)\end{array}}$

Integramos esta ecuación diferencial con las condiciones iniciales siguientes, en el instante t=0, v=v₀

${\displaystyle v=v_0-{\omega }_0^2\frac{v_0}{\omega }{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)\sin (\omega t)dt}}$

Se integra por partes

${\displaystyle \begin{array}{l}v=v_0+{v_0\exp (-\gamma t)\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)|}_0^t\\ v=v_0\exp (-\gamma t)\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)\end{array}}$

Podemos apreciar que la velocidad y la intensidad están desfasadas.

Escribiendo

${\displaystyle \cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)=\sin (\omega t+\varphi )\tan \varphi =\frac{\omega }{\gamma }}$

φ es el ángulo de desfase

Integramos de nuevo para obtener la posición x de la varilla en función del tiempo, sabiendo que en el instante t=0, parte del origen

${\displaystyle \begin{array}{l}x=v_0{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)dt}=\\ v_0\left({\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)\cos (\omega t)dt}+\frac{\gamma }{\omega }{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)\sin (\omega t)dt}\right)=\\ v_0{\left\{\frac{\omega }{{\omega }_0^2}\exp (-\gamma t)\left(\sin (\omega t)-\frac{\gamma }{\omega }\cos (\omega t)\right)-\frac{\gamma }{\omega }\frac{\omega }{{\omega }_0^2}\exp (-\gamma t)\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)\right\}|}_0^t=\\ {\frac{v_0}{{\omega }_0^2}\exp (-\gamma t)\left(2\gamma \sin (\omega t)-\frac{{\omega }_0^2}{\omega }\cos (\omega t)\right)|}_0^t\\ x=\frac{v_0}{{\omega }_0^2}\left\{2\gamma +\exp (-\gamma t)\left(\frac{{\omega }^2-{\gamma }^2}{\omega }\sin (\omega t)-2\gamma \cos (\omega t)\right)\right\}\end{array}}$

Estudio energético

La energía cinética inicial es

${\displaystyle E_0=\frac{1}{2}m{v}_0^2}$

La energía en el instante t es la suma de tres contribuciones:

• la energía cinética de la varilla

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_0^2\exp (-2\gamma t){\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)}^2=\\ \frac{1}{2}m{v}_0^2\exp (-2\gamma t)\left(\frac{1}{2}\frac{{\omega }_0^2}{{\omega }^2}+\frac{1}{2}\left(1-\frac{{\gamma }^2}{{\omega }^2}\right)\cos (2\omega t)+\frac{\gamma }{\omega }\sin (2\omega t)\right)\end{array}}$

• La energía acumulada en la autoinducción

${\displaystyle \begin{array}{l}{E}_B=\frac{1}{2}L{i}^2=\frac{1}{2}\frac{B^2{a}^2{v}_0^2}{{\omega }^{2}L}\exp (-2\gamma t){\sin }^2(\omega t)=\\ \frac{1}{4}\frac{B^2{a}^2{v}_0^2}{{\omega }^{2}L}\exp (-2\gamma t)\left(1-\cos (2\omega t)\right)\end{array}}$

• la energía disipada en la resistencia

${\displaystyle \begin{array}{l}{E}_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt}=\frac{B^2{a}^2{v}_0^2}{{\omega }^2{L}^2}R{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-2\gamma t){\sin }^2(\omega t)·dt}=\\ \frac{B^2{a}^2{v}_0^2}{{\omega }^2{L}^2}R{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-2\gamma t)\frac{1-\cos (2\omega t)}{2}·dt}=\\ \frac{B^2{a}^2{v}_0^2}{{\omega }^2{L}^2}R{\left\{-\frac{1}{4\gamma }\exp (-2\gamma t)-\frac{1}{4}\frac{\omega }{{\omega }_0^2}\exp (-2\gamma t)\left(\sin (2\omega t)-\frac{\gamma }{\omega }\cos (2\omega t)\right)\right\}}_0^t=\\ \frac{B^2{a}^2{v}_0^2}{{\omega }^2{L}^2}R\left\{\frac{1}{4\gamma }-\frac{\gamma }{4{\omega }_0^2}-\frac{1}{4\gamma }\exp (-2\gamma t)-\frac{1}{4}\frac{\omega }{{\omega }_0^2}\exp (-2\gamma t)\left(\sin (2\omega t)-\frac{\gamma }{\omega }\cos (2\omega t)\right)\right\}\end{array}}$

Comprobamos después de algunas operaciones que

E₀=E_k+E_B+E_R

Cuando t→∞, la intensidad i tiende a cero, la energía en la autoinducción E_B=0

La velocidad tiende a cero, la energía cinética final es E_k=0

La energía cinética inicial se disipa en la resistencia

${\displaystyle \begin{array}{l}{E}_R={\displaystyle \underset{0}{\overset{\infty }{\int }}{i}^{2}R·dt}=\frac{B^2{a}^2{v}_0^2}{{\omega }^2{L}^2}R{\left\{-\frac{1}{4\gamma }\exp (-2\gamma t)-\frac{1}{4}\frac{\omega }{{\omega }_0^2}\exp (-2\gamma t)\left(\sin (2\omega t)-\frac{\gamma }{\omega }\cos (2\omega t)\right)\right\}}_0^{\infty }=\\ \frac{B^2{a}^2{v}_0^2}{{\omega }^2{L}^2}R\left\{\frac{1}{4\gamma }-\frac{\gamma }{4{\omega }_0^2}\right\}=\frac{B^2{a}^2{v}_0^2}{4{\omega }^2{L}^2}R\frac{{\omega }^2}{{\omega }_0^2\gamma }=\frac{1}{2}m{v}_0^2\end{array}}$

Casos particulares

R=0, L≠0

Tenemos oscilaciones armónicas de frecuencia ω₀

${\displaystyle \begin{array}{l}i=\frac{Ba{v}_0}{{\omega }_{0}L}\sin ({\omega }_{0}t)\\ v=v_0\cos ({\omega }_{0}t)\\ x=\frac{v_0}{{\omega }_0}\sin ({\omega }_{0}t)\end{array}}$

La suma de la energía cinética y la energía acumulada en la autoinducción es constante e igual a la energía cinética inicial. La autoinducción acumula energía potencial en forma de energía asociada al campo magnético.

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}m{v}_0^2{\cos }^2({\omega }_{0}t)\\ E_B=\frac{1}{2}L\frac{B^2{a}^2{v}_0^2}{{\omega }_0^2{L}^2}{\sin }^2({\omega }_{0}t)=\frac{1}{2}m{v}_0^2{\sin }^2({\omega }_{0}t)\end{array}}$

L=0, R≠0

La ecuación del circuito es

iR-Bav=0

La ecuación del movimiento de la varilla

${\displaystyle m\frac{dv}{dt}=-iBa}$

Combinando ambas ecuaciones e integrando

${\displaystyle \begin{array}{l}\frac{dv}{dt}=-\frac{B^2{a}^2}{mR}v\\ \frac{dv}{v}=-\frac{B^2{a}^2}{mR}dt\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{v}=}-\frac{B^2{a}^2}{mR}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ v=v_0\exp (-kt)k=\frac{B^2{a}^2}{mR}\\ i=\frac{Ba}{R}{v}_0\exp (-kt)\end{array}}$

La posición x de la varilla en función del tiempo t es

${\displaystyle x={\displaystyle \underset{0}{\overset{t}{\int }}v·dt}={\displaystyle \underset{0}{\overset{t}{\int }}{v}_0\exp (-kt)·dt}=\frac{v_0}{k}\left(1-\exp (-kt)\right)}$

La energía cinética inicial de la varilla, se disipa en la resistencia

${\displaystyle E_0=\frac{1}{2}m{v}_0^2}$

Energía cinética de la varilla en el instante t

${\displaystyle E_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_0^2\exp (-2kt)}$

Energía disipada en la resistencia

${\displaystyle E_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt}=\frac{B^2{a}^2}{R}{v}_0^2{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-2kt)·dt}=\frac{1}{2}m{v}_0^2\left(1-\exp (-2kt)\right)}$

Como podemos comprobar E₀=E_k+E_R

Cuando t→∞, la energía cinética inicial se disipa en la resistencia.

Ejemplo

• Coeficiente de autoinducción, L=0.08 H
• Resistencia, R=0.02 Ω
• Campo magnético, B=1.0 T
• Masa de la varilla, m=0.1 kg
• Distancia entre los raíles, a=0.5 m
• Velocidad inicial, v₀=1.0 m/s

Calcular la intensidad i, la velocidad v de la varilla y su posición x en el instante t=0.5 s

Las fórmulas que tenemos que emplear son

${\displaystyle \begin{array}{l}\gamma =\frac{R}{2L}{\omega }_0^2=\frac{B^2{a}^2}{mL}{\omega }^2={\omega }_0^2-{\gamma }^2\\ i=\frac{Ba{v}_0}{\omega L}\exp (-\gamma t)\sin (\omega t)\\ v=v_0\exp (-\gamma t)\left(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)\\ x=\frac{v_0}{{\omega }_0^2}\left\{2\gamma +\exp (-\gamma t)\left(\frac{{\omega }^2-{\gamma }^2}{\omega }\sin (\omega t)-2\gamma \cos (\omega t)\right)\right\}\end{array}}$

i=0.357 A, v=-0.876 m/s, x=0.07 m

Balance energético

Energía inicial

${\displaystyle E_0=\frac{1}{2}m{v}_0^2=\frac{1}{2}0.1·1^2=0.05\text{J}}$

La energía del campo magnético en la autoinducción es

${\displaystyle E_B=\frac{1}{2}L{i}^2=\frac{1}{2}0.08·{0.357}^2=0.0051\text{J}}$

La energía cinética de la varilla es

${\displaystyle E_k=\frac{1}{2}m{v}^2=\frac{1}{2}0.1·{0.857}^2=0.0384\text{J}}$

La energía disipada en la resistencia es la diferencia

E_R=E₀-E_k-E_B=0.0065 J

Se puede comprobar que sale este resultado en la larga expresión de la energía disipada en la resistencia

${\displaystyle E_R=\frac{B^2{a}^2{v}_0^2}{{\omega }^2{L}^2}R\left\{\frac{1}{4\gamma }-\frac{\gamma }{4{\omega }_0^2}-\frac{1}{4\gamma }\exp (-2\gamma t)-\frac{1}{4}\frac{\omega }{{\omega }_0^2}\exp (-2\gamma t)\left(\sin (2\omega t)-\frac{\gamma }{\omega }\cos (2\omega t)\right)\right\}}$

Actividades

Se introduce

• El campo magnético B ( T), en el control de edición titulado Campo magnético.  Se pueden introducir valores positivos o negativos
• El coeficiente de autoinducción L (H), en el control de edición titulado Autoinducción
• La resistencia R (Ω) de la porción de varilla de longitud a, en el control de edición titulado Resistencia. El resto del circuito se considera superconductor
• La velocidad inicial se ha fijado en v₀ =1 m/s
• La distancia entre los raíles se ha fijado en a=0.5 m
• La masa de la varilla m (kg) en el control de edición titulado Masa

Se pulsa el botón titulado Empieza

En la parte superior del applet se representa, la bobina, los raíles y la varilla.

Al lado de la bobina se proporciona el dato de la intensidad en A

El campo magnético uniforme es perpendicular al plano de los raíles, apunta hacia el lector cuando está coloreado de rosa, y en sentido contrario si está coloreado de azul claro.

Al lado de la varilla se proporciona el dato de su posición

Un diagrama en forma de tarta, nos da una idea de la transformaciones energéticas.

• Un sector de color rojo, representa la energía almacenada en la autoinducción
• Un sector de color azul, representa la energía cinética de la varilla
• Un sector de color negro, representa la energía disipada en la resistencia

En la parte derecha del gráfico, se representa la velocidad v de la varilla en función del tiempo. Podemos apreciar, que representa una oscilación amortiguada.

El programa interactivo, no trata el caso de que la autoinducción sea nula, L=0, se estudia en la página Efectos mecánicos de la ley de Faraday" pero si el caso de que la resistencia sea nula R=0.

Tampoco trata las oscilaciones críticas y sobreamortiguadas, cuando γ≥ω₀. Se estudian en la página "Efectos mecánicos de la ley de Faraday. Oscilaciones amortiguadas"

FemApplet aparecerá en un explorador compatible JDK 1.1

Referencias

Hecking P., Energy ambiguity and the inductive rail oscillator. The Physics Teacher Vol 45, October 2004, pp. 445-449

Curso Interactivo de Física en Internet © Ángel Franco García