• Inicio
• Electromagnetismo
• Campos dependientes del tiempo
• Inducción mutua y autoinducción

Solenoide de longitud variable

En la página “Condensador plano-paralelo” estudiamos los cambios energéticos que ocurrían cuando se desplazaba una de las placas del condensador plano-paralelo conectado a una batería.

Las placas de signos opuestos se atraen, con una fuerza que hemos calculado ½qE, la mitad del producto de la carga q de las placas por el campo eléctrico uniforme existente E entre las placas.

El solenoide está formado por espiras. Cuando la corriente pasa por el solenoide las espiras se atraen, debido a que las corrientes circulan en el mismo sentido. Resulta complicado calcular la fuerza de atracción entre las espiras. La fuerza F (véase la figura) que tenemos que ejercer para incrementar la separación entre las espiras, es decir, la longitud del solenoide se puede calcular de forma indirecta.

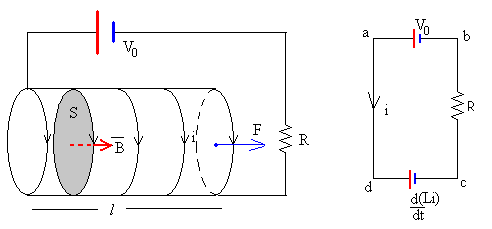
Cuando se conecta una batería V₀ a una resistencia R y una autoinducción L, la corriente se incrementa, la autoinducción se comporta como una batería V_L que se opone al incremento de la corriente, el circuito equivalente de la parte derecha de la figura.

${\displaystyle V_L=-\frac{d\Phi }{dt}=-\frac{d(Li)}{dt}}$

donde la autoinducción L ahora no es constante.

La ecuación del circuito

${\displaystyle \begin{array}{l}{V}_{ab}+V_{bc}+V_{cd}+V_{da}=0\\ V_0-iR-\frac{d(Li)}{dt}=0\end{array}}$

Multiplicando por la intensidad,

${\displaystyle V_{0}i=i^{2}R+i\frac{d(Li)}{dt}}$

Teniendo en cuenta que

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{1}{2}L{i}^2\right)=\frac{1}{2}{i}^2\frac{dL}{dt}+Li\frac{di}{dt}\\ i\frac{d(Li)}{dt}=i^2\frac{dL}{dt}+Li\frac{di}{dt}\end{array}}$

Tenemos la relación

${\displaystyle i\frac{d(Li)}{dt}=i^2\frac{dL}{dt}+\frac{d}{dt}\left(\frac{1}{2}L{i}^2\right)-\frac{1}{2}{i}^2\frac{dL}{dt}=\frac{d}{dt}\left(\frac{1}{2}L{i}^2\right)+\frac{1}{2}{i}^2\frac{dL}{dt}}$

La ecuación de la energía del circuito se escribe

${\displaystyle V_{0}i=i^{2}R+\frac{d}{dt}\left(\frac{1}{2}L{i}^2\right)+\frac{1}{2}{i}^2\frac{dL}{dt}}$

• El primer término, es la energía por unidad de tiempo suministrada por la batería

• El segundo, es la energía por unidad de tiempo, que se pierde en la resistencia

• El tercer término, es la energía por unidad de tiempo que se acumula en la autoinducción en forma de campo eléctrico.

• El cuarto término, ha de ser la energía por unidad de tiempo suministrada por la fuerza externa  F aplicada (potencia).

${\displaystyle -\frac{1}{2}{i}^2\frac{dL}{dt}=Fv}$

La batería y el trabajo de la fuerza externa contribuyen, por una parte, a incrementar la energía del campo magnético en el interior del solenoide y por la otra a calentar la resistencia.

En el caso de un solenoide de longitud l, formado por N espiras de sección S

${\displaystyle L=\frac{{\mu }_0{N}^{2}S}{l}\frac{dL}{dt}=-{\mu }_0\frac{N^2}{l^2}S\frac{dl}{dt}=-{\mu }_0\frac{N^2}{l^2}Sv}$

Despejamos la fuerza F

${\displaystyle F=\frac{1}{2{\mu }_0}{\left({\mu }_0\frac{Ni}{l}\right)}^{2}S=\frac{1}{2{\mu }_0}{B}^{2}S}$

Donde el término entre paréntesis es precisamente el campo magnético en el interior de un solenoide.

Un argumento similar, se puede emplear para determinar la fuerza necesaria para incrementar la sección S de las espiras, manteniendo constantes la longitud del solenoide y el número de espiras.

Referencias

Blanchard C. H. Magnetic pressure and tension via the solenoid. Am .J Phys. 44 (9) September 1976, pp. 891-892

Curso Interactivo de Física en Internet © Ángel Franco García